La face cachée du Rubik's Cube

En Rubik's Cube il y a deux notions très importantes à comprendre: la notion de configuration et la notion de formule . Comme en géométrie avec la notion de 'point', on voit bien ce qu'est un 'point', mais l'expliquer n'est pas évident ! Même chose ici, on voit ce qu'est une configuration et une formule mais les expliquer c'est autre chose.

Les configurations G⁺

Prenez un Rubik's Cube standard, orientez le, c'est-à-dire dire qui est le Haut, qui est l'Avant .... pour nous ça sera:
H(aut)=b(lanc), B(as)=j(aune), A(vant)=v(ert), P(ostérieur)=k(lein), G(auche)=o(range), D(roite)=r(ouge)

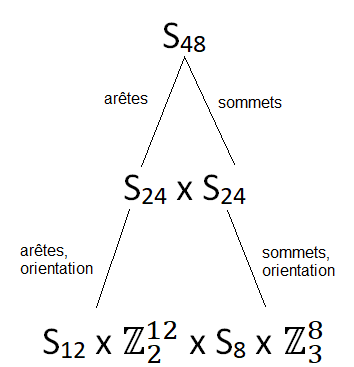
1. Les arêtes et les sommets forment deux clans bien distigues , ils ne se mélangent jamais, une arête ne se met pas à la place d'un sommet et inversement (c'est normal, car physiquement ces pièces sont différentes).

2. On peut permuter ces 12 arêtes entre elles comme on veut, on a donc affaire à S₁₂ (le groupe des permutations à 12 objets) et chaqu' arête possède 2 orientations. donc l'orientation des arêtes est codée par un vecteur à 12 composantes à valeur dans {0,1}, on a affaire à Z₂¹² (Z₂ = un groupe à 2 éléments), finalement pour les arêtes on a S₁₂ x Z₂¹²

3. Même chose pour les sommets
On peut permuter les 8 sommets entre eux comme on veut, on a donc affaire à S₈ et chaque sommets possède 3 orientations. donc l'orientation des sommets elle aussi est codée par un vecteur à 8 composantes à valeur dans {0,1,-1}, on a affaire à Z₃⁸, pour les sommets on a S₈ x Z₃⁸

Finalement on pose :

G⁺ = (S₁₂ x Z₂¹²) x (S₈ x Z₃⁸)
C'est l'ensemble des configurations

voici visuellement quelques configurations

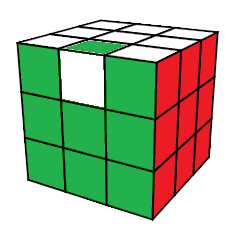
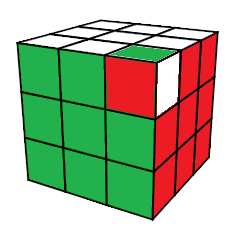
Une configuration	Une autre configuration

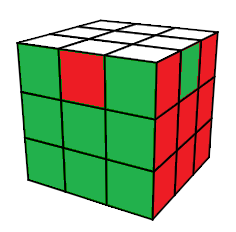
Une configuration	Une autre configuration

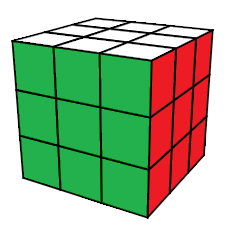Une configuration	configuration résolue (une couleur par face)

Une configuration est une sorte de motif des autocollants
On remarque que les centres ne sont pas bougés : Haut=blanc, Bas=jaune, Avant=vert, ...

La loi interne '.' dans G⁺:

On va définir une loi '.' dans G⁺ :
s=(u,x,v,y) et s'=(u',x',v',y')
ss' = (u,x,v,y)(u',x',v',y') = (uu', x+u(x'), vv', y+v(y'))
où p(x) = (x_p(1), x_p(2),..., x_p(n)) ; p=permutation, x=vecteur
uu' = u'o u
(G⁺, .) est un groupe

une "configuration" est mathématiquement représentée par (u,x,v,y) un 4-uplet

Un exemple :
pour les arêtes
u = (1,3,5,2)(9,11) et x = (x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁, x₁₂)
u(x) = (x₃, x₁, x₅, x₄, x₂, x₆, x₇, x₈, x₁₁, x₁₀, x₉, x₁₂)
on permute les x_i par u.

-On a: u(x+x') = u(x) + u(x')

-Parfois on note: 0 = (0,0,...,0) , 1 = (1,1,...,1)
ex (id,0,id,1) ==>
id=permutation identique
0=(0,0,0,0,0,0,0,0,0,0,0,0) vecteur nul
id=identité
1=(1,1,1,1,1,1,1,1) vecteur ayant des 1

Les formules M

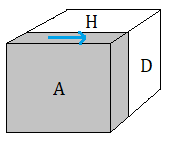
On prend un Rubik's Cube monochrome et on le pose sur une table avec une face devant nous, on a donc 6 faces ainsi nommées:
H(aut), B(as), A(vant), P(ostérieur), G(auche), D(roite)

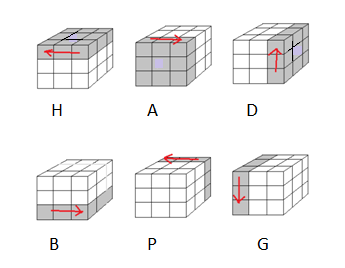
Rubik's Cube monochrome	les rotations de base

Et les 6 rotations de base: {H, B,A,P,G,D}
A = on tourne la face A 90° dans le sens horaire
A' = on tourne la face A -90° (dans le sens antihoraire)
A² = on tourne la face A 180°

On pose :
M = < H,B,A,P,G,D > , M est engendré par les 6 rotations de base {H,B,A,P,G,D}
M c'est l'ensemble des formules
Une formule est donc une suite finie de rotations de base avec la règle :
HH', H'H, BB',B'B, etc ....est interdit dans une formule

ex:
HDB²PA'GH'D' ==> OK
GHDD'GB'P² ==> interdit à cause DD'

Remarque : M est infini car on peut écrire : AAA, AAAAAA, AAAAAAAAA, ....

Une loi '.' dans M

On définit une loi '.' dans M: '.' = la concaténation : V, T ==> VT
On pose : HH' = H'H = BB' = B'B = etc ....= I
(M, .) forme un groupe en effet

(i) V,T ∈M ==> VT∈M ; loi interne
(ii) IV = VI = V ; I élément neutre
(iii) V = HBA'DGP²D' ==> V' = DP'²G'D'AB'H' ; inverse
(iv) (VT)S = V(TS) ; associative

Action '•' de M sur G⁺

On définit une action '•' de M dans G⁺ ainsi
G⁺ x M --> G⁺
(s,V) --> s•V = t
Vérifiant les axiomes suivants:
A₁ : s•I = s ; élément neutre
A₂ : (s•V)•T = s•(VT) ; associativité
A₃ : a donné,fixé
a•V = a ==> V=I ; librement
A₄ : s•(VT) = (s•V)(s•T) ; compatibilité

Remarque : (i) l'Axiome3 montre que deux formules donnant une même configuration seront considérés comme identiques
en effet :
a donné, fixé
a•V = a•T
(a•V)•T' = (a•T)•T'
a•(VT') = a•(T•T')
a•(VT') = a•I = a
a•(VT') = a
VT' = I ==> V = T ; (A3)

Exemples:
A' = A³
A⁴ = I
A'B²AH²A'B²AH² = H²DBD'H²DB'D'
A⁴ = D⁴
(H²D²)³(B²D²)³ = (H²G²)³(B²G²)³
B = (DG'A²P²DG') H (DG'A²P²DG')

(ii) L'axiome3 rend M fini .
On a vu qu'on peut écrire :
A', AAA, AAAAAA, .... M aura donc une infinité d'éléments, or on sait que le groupe du Rubik's Cube est fini, on aimerait donc que M lui aussi soit fini, et avoir le même nombre d'éléments que le goupe du Rubik's Cube. Pour arriver on doit passer par ce qu'on appelle le groupe libre ....

Groupe libre

On se donne 2 ensembles finis X={a,b,c,d,...}, X'={a',b',c',d',...} disjoints et en bijection a -> a' , b -> b'... et un élémént 1 non dans X et X'. On forme les mots de X c'est-à-dire les suites finies d'éléments de X et X' avec la règle: aa', a'a, bb', b'b, cc', c'c, ... interdits
du genre

V = abd'b²c ; OK
T = c'dab'bd² ; interdit à cause b'b

Soit F_X l'ensemble des mots de X ,
On pose :
aa' = a'a = bb' = b'b = cc' = c'c ... = 1
et on prend par définition :
1. 1 = élément neutre,
2. a' ==> symétrique de a
3. V=ab'dc ==> V'=c'd'ba' symétrique de V
4. F_X muni la loi concaténation :
V,T ∈F_X ==> VT = N (on supprime bien sûr les a'a, aa', b'b, bb', .... dans N)
V = acb'd , T = d'cb²a ==> VT = acb'dd'cb²a = acb'cb²a
F_X forme ainsi un groupe nommé groupe libre engendré par X

Soit maintenant L un groupe fini, et f un morphisme injective de F_X -> L :
f: F_X -> L ; f injectif
V -> f(V)
et une relation d'équivalznce
V,T ∈F_X , V~T ssi V,T ∈Ker(f)
alors on a:
F_X/~ = F_X/Ker(f) = F_X ≅ Im(f) (th: F_X/Ker(f) ≅ Im(f))

Pour nous
X = {H,B,A,P,G,D} , F_X = M
L = G⁺
f: M -> G⁺
f(V) = e•V ; e=état résolu
V,T ∈M , V~T ssi V,T ∈Ker(f))
et M/~ = M/Ker(f) = M ≅ Im(f) ⊂ G⁺ fini

il est plus facile, et plus compréhensible de manipuler
M = < H, B, A, P, G, D > ; avec la convention V=T si V,T donnent la même configuration
que de manipuler des classes d'équivalences.
M/~

Remarque

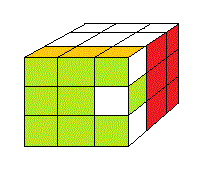
ΓA signifie on fait la rotation Γ puis la rotation A et ΓA ≠ AΓ

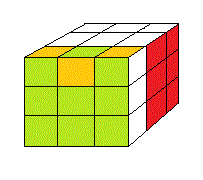ΓA	AΓ

Le groupe du Rubik's Cube (G, .)

Par définition le groupe du Rubik's Cube est :
G = {s∈G⁺ / s=e•V , V∈M} , e=état résolu
Ce sont des configurations provenant de M (à partir de e), les éléments de G se nomment les états,
G est un sous groupe de G⁺

Théorème fondamental de la Cubologie

On se pose la question suivante : Quelles sont les conditions nécessaires et suffisantes pour qu'une configuration soit un état ?
On pose :
s=(u,x,v,y) ∈G⁺ avec:
(F) x=0 (mod 2)
(T) y=0 (mod 3)
(P) sig(u) = sig(v)

On démontre alors le théorème suivant:
G = {s∈G⁺ / s vérifie (F), (T), (P)}
Ce sont des configurations vérifiant (F), (T), (P),

Les rotations étendues

Rotation Γ : pivoter une arête .
1. On enlève l'arête (HA)
2. La pivote (180° ou -180°)
3. Puis on la remet

Rotation étendue Γ

Par définition ce manoeuvre se nomme rotation étendue Γ qui a comme résultat , l'arête (HA) est pivotée (180° ou -180°)
(HA)° = (HA)⁺ = (HA)^- = Γ

Rotation Ψ : pivoter un sommet .
1. On enlève le sommet (HDA)
2. Le pivote 1/3 tour dans le sens horaire (120°)
3. Puis on le remet

Rotation étendue Ψ

Ce manoeuvre , par définition , se nomme rotation étendue Ψ qui a comme résultat, le sommet (HDA) pivoté 1/3 de tour dans le sens horaire (120°)
(HDA)⁺ = Ψ

Rotation Ω : permuter deux arêtes .
1. On enlève les arêtes (HA), (HD)
2. Permute (HA)<->(HD) = (HA,HD)
3. Puis on les remet

rotation étendue Ω

Ce manoeuvre , par définition , se nomme rotation étendue Ω qui a comme résultat, les arêtes (HA) , (HD) sont permutées
(HA)<->(HD) = (HA,HD) = Ω

Ce sont des manoeuvres impossible à réaliser sans enlever les pièces.
Les "rotations" Γ, Ψ, Ω , par définition appellées rotations étendues (les rotations étendues sont des rotations qui violent les lois de Rubik's Cube).
On note M⁺ l'ensemble des formules étendues
M⁺ = < H, B, A, P, G, D ,Γ, Ψ, Ω > , M⁺ est donc engendré par les 6 rotations de base et les 3 rotations étendues.
Rappel : deux formules donnant la même configuration seront considèrées comme identiques.
M ⊂ M⁺

Le groupe (M⁺, .)

L'ensemble des formules étendues M⁺ muni la concaténation '.' de deux formules forme un groupe (M⁺, .) , en effet on a:
M = < H,B,A,P,G,D > (engendré par {H, B, A, P, G, D}) est un sous groupe de M⁺ .

Finalement : il y a 2 concepts importants il faut bien comprendre et maitriser et ne pas confondre.
concept: configuration (==> état)
concept: formule

L'ensemble X des autocollants

Soit X = {1,2,3, ..., 48} l'ensemble des autocollants numérotées comme indique la fig ci-dessous
Notre but c'est de numéroter les autocollants de telle sorte qu'on puisse les regrouper facilement pour former les arêtes et les sommet
*Pour les arêtes: les autocollants pairs .
On commence par les facettes dominantes : 2,4,6,8, ...
Puis les autres facettes

*Pour les sommets: les autocollants impairs .
On commence par les facettes dominantes : 1,3,5,7, ...
Puis les autres facettes dans le sens horaire.

x_i = (2i, 2i+24) , y_i = (2i-1, 4i+13, 4i+15)

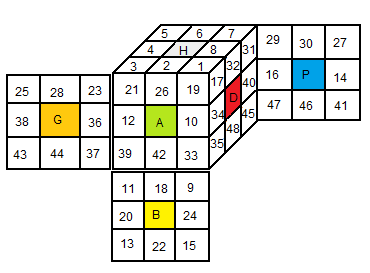L'ensemble des autocollants X	L'ensemble des autocollants X

Action du groupe M sur X

D'un côté on a un Rubik's Cube monochrome, de l'autre côté les autocollants numérotés éparpillées sur la table, physiquement rien ne lie entre ces deux objets. Imaginez lorsqu'on fait une rotation A par ex, une force mystérieuse déplace les autocollants ....

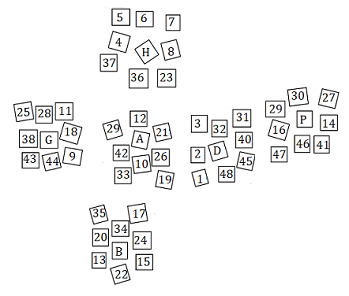Rotation A	autocollants déplacées

On appelle ceci "action" de A sur X, Ce n'est pas A qui déplace les autocollants mais une permutation p_A de X, un élément de S_x , p_A∈S_x , la rotation A ordonne à p_A de déplacer les autocollants. au lieu de prendre la rotation A, on peut prendre n'importe quel élément de M, on dit que M agit sur X

A chaque rotation de base {H,B,A,P,G,D} on associe une permutation {p_H, p_B, p_A, p_P, p_G, p_D} de S_x et soit Λ les permutations engendrées par {p_H, p_B, p_A, p_P, p_G, p_D}
Λ = < p_H, p_B, p_A, p_P, p_G, p_D > et
Λ⁺ = < p_H, p_B, p_A, p_P, p_G, p_D, p_Γ, p_Ψ, p_Ω >

Permutations standards (arête,sommet)
p_H = (2,4,6,8)(26,28,30,32) (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
p_B = (18,24,22,20)(42,48,46,44) (9,15,13,11)(33,45,41,37)(35,47,43,39);
p_A = (2,34,18,36)(26,10,42,12) (1,35,11,23)(17,9,37,3)(19,33,39,21);
p_P = (6,38,22,40)(30,14,46,16) (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
p_G = (4,12,20,14)(28,36,44,38) (3,39,13,27)(21,11,41,5)(23,37,43,25);
p_D = (8,16,24,10)(32,40,48,34) (1,29,15,33)(17,31,45,35)(19,7,47,9);

Permutations étendues
p_Γ = (2,26);
p_Ψ = (1,17,19);
p_Ω = (2,8)(26,32);

Permutations tranches
p_h = (10,36,14,40)(34,12,38,16);
p_d = (2,30,22,42)(26,6,46,18);
p_a = (4,32,24,44)(28,8,48,20);

Le GAP
Télécharger le GAP .::ICI::. https://www.gap-system.org/Releases/4.4.12.html
Dans la fenêtre de cmd on se place dans le dossier de GAP
C:\Users\nom> cd\gap4r4\bin
C:\gap4r4\bin>gap < gap_rubikcube.txt

fichier gap_rubikcube.txt
gap_rubikcube.txt

pH := (2,4,6,8)(26,28,30,32) (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
pB := (18,24,22,20)(42,48,46,44) (9,15,13,11)(33,45,41,37)(35,47,43,39);
pA := (2,34,18,36)(26,10,42,12) (1,35,11,23)(17,9,37,3)(19,33,39,21);
pP := (6,38,22,40)(30,14,46,16) (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
pG := (4,12,20,14)(28,36,44,38) (3,39,13,27)(21,11,41,5)(23,37,43,25);
pD := (8,16,24,10)(32,40,48,34) (1,29,15,33)(17,31,45,35)(19,7,47,9);
pGamma := (2,26);
pPsi := (1,17,19);
pOmega := (2,8)(26,32);
ph := (10,36,14,40)(34,12,38,16);
pd := (2,30,22,42)(26,6,46,18);
pa := (4,32,24,44)(28,8,48,20);
Lambdaplus := Group( pH, pB, pA, pP, pG, pD, pGamma, pPsi, pOmega );
Lambda1 := Group( pH, pB, pA, pP, pG, pD );
Print( "\n" );
Print( "|Lambda+| = ",Size( Lambdaplus ), "\n" );
Print( "|Lambda| = ", Size( Lambda1 ) , "\n" );
Print( "N = ", 2 * 3 * 2 , "\n" );
Print( "|G+| = ", Factorial(12) * 2^12 * Factorial(8) * 3^8 , "\n" );
Print( "|G| = |G+|/N = ", Factorial(12) * 2^12 * Factorial(8) * 3^8 / ( 2 * 3 * 2 ), "\n" );

Les permutations de Λ : p_H, p_B, ... ∈S_x ne sont pas quelconque de X mais elles sont très particulières pour voir celà il suffit de suivre le mouvement des autocollants, l'autocollant '1' par exemple, elle ne peut pas se placer en '34' par ex , ou encore à chaque fois que '1' bouge , l'autocollant '17' bouge aussi... le '1' a un mouvement de S₈ et de rotation autour d'un triangle équilatérale (le '1' peut se placer en '17' ou '19'). Ainsi On peut regrouper les autocollants en arêtes et en sommets et leurs orientations pour former une configuration s:


s = (u,x,v,y) avec u∈S₁₂, x∈Z₂¹², v∈S₈, y∈Z₃⁸
On retrouve ainsi :
G⁺ = (S₁₂ x Z₂¹²) x (S₈ x Z₃⁸)

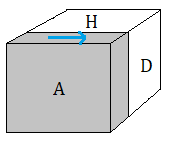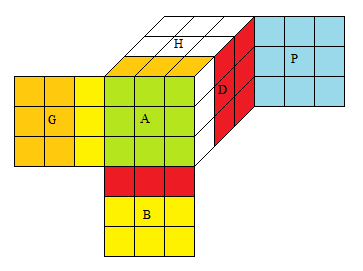Rotation A	état

Il est donc important de faire la distinction entre: configuration, formule, permutation, .
G⁺ c'est l'ensemble des configurations, cet ensemble forme un groupe . G c'est l'ensemble des configurations produites par les rotations de base {H,B,A,P,G,D}, c'est un sous-groupe de G⁺

G = {s∈G⁺ / s=e•V , V∈M} , e=état résolule , le groupe du Rubik's Cube
G⁺ = le groupe étendu de G

3 antagonismes M, Λ, G

L'étude mathématique du Rubik's Cube fait intervenir 3 antagonismes M, Λ, G , on va voir le rôle de chaqu'un
M = <H, B, A, P, G, D> , le groupe des formules (M ⊂ M⁺)
Λ = <p_H, p_B, p_A, p_P, p_G, p_D> , le groupe des permutations des 48 autocollants (Λ ⊂ S₄₈)
G = le groupe du Rubik's Cube (G ⊂ G⁺) , G = {s∈G⁺ / s=e•V , V∈M} , e=état résolu
Tous les 3 sont isomorphes, mais on ne peut pas les identifiés car chaqu'un joue un rôle différent .

-M agit sur G
-M agit sur X
Beaucoup d'auteurs définissent Λ comme le groupe du Rubik's Cube mais ce n'est pas la discription la plus visuelle
Pour nous le groupe du Rubik's Cube c'est G l'ensemble des configurations provenant de M.

V : formule	pV : permutations

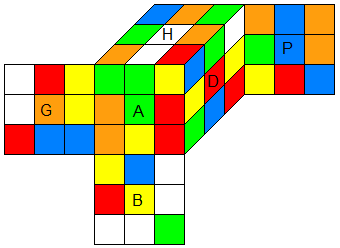s=e•V : état

On a:
Λ⁺ <== M⁺ ==> G⁺
Λ <== M ==> G

Voici la démarche :

1. G⁺ = S₁₂ x Z₂¹² x S₈ x Z₃⁸ les configurations
2. Loi interne '.' sur G⁺ : (u,x,v,y)(u',x',v',y') = (uu', x+u(x'), vv', y+v(y'))
3. M = < H,B,A,P,G,D > les formules
4. (M, .) : '.' concaténation
5. Action '•' de M sur G⁺
6. Définition de G: G = {s∈G⁺ / s=e•V , V∈M} , e=état résolu
7. Théorème fondamental : G = {s∈G⁺ / s vérifie les 3 lois}

Remarque
M = < H,B,A,P,G,D >
On peut avoir 5 générateurs
M = < H,A,P,G,D > où B = (DG'A²P²DG')H(DG'A²P²DG') (Roger Penrose)
On peut avoir 2 générateurs
M = < Q,K > où Q = HPGHG'H'P' et K = D²AGB'D' (Frank Barnes)

[1] 2 3 4 5 6 7 8 9

Accueil

DMJ: 20/05/2025