Le Pyraminx
11
Dec
2012
Pyraminx (tétraèdre)
Inventeurs: Uwe MEFFERT
Année: 1971
Nombre d'états: 6!.26 x 34 x 34/2x2 = 75582720
Loi de parité : oui
¤ sig(arêtes) = 1
Loi des flips : oui
¤ ∑ arêtes = 0 (mod 2)
Diamétre: 11 (sans sommets)
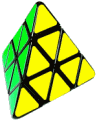
Le Pyraminx est un tétraèdre dont chaque face portant une couleur, il est composé de 22 petits triangles. Lorsqu'on mélange le puzzle les petits triangles se déplacent
ce qui fait que les faces perdent sa couleur initiale (en sortant de l'usine). Le but c'est de reconstituer le Pyraminx à l'état d'origine, chaque face portant une seule couleur.
Commentaire
- Le Pyraminx vérifie la formule d'Euler:
F = nombre de faces, S = nombre de sommets, A = nombre d'arêtes .
F = 4, S = 4, A = 6
- Pyraminx* = Pyraminx (son propre dual)
- Le nombre de stickers sur une face:
1+3+5 = 3²
C'est la somme des n nombres impairs consécutifs
Nombre d'états:
==> Si on ne veut pas compter les sommets , chaque sommet a 3 orientations , comme on a 4 sommets, on a donc 34 = 81
75582720/34 = 933120 (arêtes+centres = le groupe Slice)
==> Si on ne veut pas non plus compter centres, les 3 centres autour d'un sommet forment un gros sommet à 3 orientations, comme on a 4 gros sommets on a donc 34 = 81
933120/34 = 11520 (arêtes)
Un programme d'informatique nous montre que le diamètre du Slice groupe du Pyraminx (sans sommets) vaut 11:
Distance: nombre d'états (arêtes+centres)
0: 1
1: 8
2: 48
3: 288
4: 1728
5: 9896
6: 51808
7: 220111
8: 480467
9: 166276
10: 2457
11: 32
============
Total: 933120
1- Notation
Nom des pièces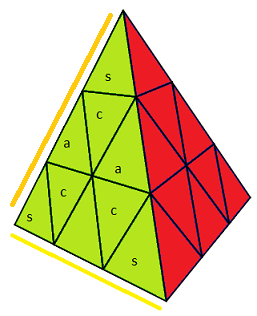
 |
|
| s=sommet, c=centre, a=arête |
|
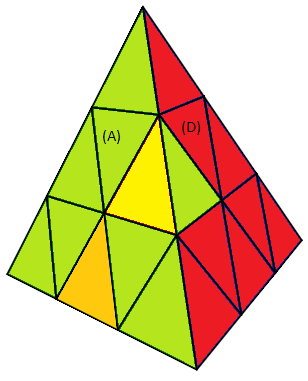
Les faces seront notées entre parenthèses: (A)=face Avant, (G)=face Gauche, (D)=face Droite, (B)=face Bas
Rotations sommets
Les sommets seront notés sans parenthèses: (BGA)=G, sommet G (rotation G)
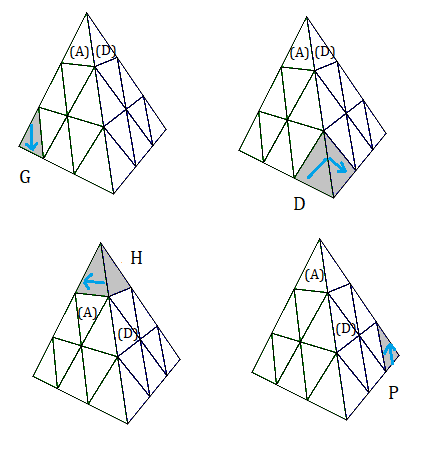
Voici les rotations (par rapport aux sommets) utilisées:
G(auche), D(roite), H(aut), P(ostérieur).
(BGA) = G, (BAD) = D, (AGD) = H, (BDG) = P
G = tourner 120° dans le sens des aiguilles d'une montre.
G' = tourner 120° dans le sens contraire (-120°)
G² = tourner 240°
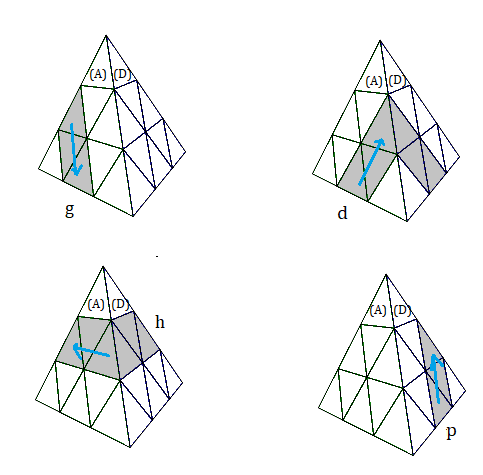
Rotations tranches
g = tourner 120° dans le sens des aiguilles d'une montre.
g' = tourner 120° dans le sens contraire (-120°)
g² = tourner 240°
 |
|
| Rotations sommets |
|
 |
|
| Rotations tranches |
|
On écit (AG) pour désigner l' arête Avant-Gauche
(AG)° = pivoter l' arête (AG)
Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!
2- Observation
Comme nous avons déjà dit plus haut, le Pyraminx est formé par 22 petits triangles divisé en 3 catégories:
1. Les centres (12) : portant une seule couleur, ils se regroupent 3 par face , ils bougent un peu !
2. Les arêtes (6): portant 2 couleurs, elles se déplacent librement, et ont 2 orientations.
3. Les sommets (4): portant 3 couleurs, ils ne se déplacent pas mais peuvent se pivoter, mais pratiquement ils ne servent à rien !!!.
Mais les arêtes ne se mettent jamais à une place des sommets, ou des centres et inversement. Chaqu'un reste dans son groupe,
les arêtes dans le groupe des arêtes, les sommets dans le groupe des sommets, les centres dans le groupe des centres.
 |
|
| Essayez: [gd'] = gd'g'd |
|
[1] 2
Accueil
DMJ: 11/10/2024
