Le Fisher's Cube
| Difficulté: 12.5/20 moyen |
|
|
21
Dec
2013
Fisher's Cube
Inventeurs: Tony Fisher
Année: 1985
Nombre d'états:
Loi de parité: oui
Loi d'orientation: oui
Loi des centres: oui
Tony Fisher est un grand créateur de cubes, c'est lui qui a crée le fameux Golden Cube et le Golden Egg ... Le Fisher's Cube possède des caractéristiques vraiment étonnantes !!
- Peut générer des singularités.
- Change de formes après un mélange
- Les centres pivotent
Le fait de modifier le "design" (les lignes de rotations), rend le cube vraiment joli et la résolution est bien difficile ...
Commentaire
Le Fisher a un core 3x3x3 càd un Rubik's Cube déguisé il possède donc les fameuses 3 lois du Rubik's Cube, en plus comme les centres sont orientés il possède
aussi la loi des centres
Rappel la loi des centres:
Soit k le nombre de pivotement des centres à 90°, alors par définition la direction des centres est:
dir(centres) = dir(c) = (-1)k
Loi des centres: sig(sommets) = dir(centres)
Autrement dit la loi des centres dit: à l'état résolu on a:
- Deux centres, l'un à 90° et l'autre -90°
ou
- Un centre à 180°
1- Notation
On va nommer les faces et les couleurs ainsi:
H(aut)=b(lanc) , B(as)=j(aune) , A(vant)=v(ert) , P(ostérieure)=k(lein) , G(auche)=o(range) , D(roite)=r(ouge)
d(droite-intérieur) .
Les rotations
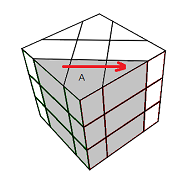
A = tourner 90° la face Avant dans le sens des aiguilles d'une montre.
A' = tourner 90° dans le sens contraire
A² = tourner 180°
D* = tourner le bloc Droite
d = droite-intérieur (d=D*D')
Dans les dessins 3D, la face Haut
a le carré blanc .
On écit (HA) pour désigner l'arête Haut-Avant ou (HDA) le sommet Haut-Droite-Avant
(HA)° = pivoter l'arête (HA)
(HDA)° = pivoter le sommet (HDA)
Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!
 |
 |
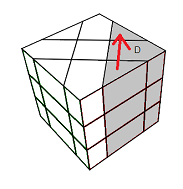| Rotation A |
Rotation D |
2- Observation
Le Fisher's Cube est formé par des pièces divisées en 3 catégories:
1. Les centres (6) : 2 portant une seule couleur (non orienté), 4 à deux couleurs (orientés), ils pivotent.
2. Les arêtes (12): 8 portant 2 couleurs (orientés), 4 une seule couleur (non orientés), elles se déplacent.
3. Les sommets (8): portant 2 couleurs (3 orientations), ils se déplacent aussi
Les arêtes ne se mettent jamais à la place des sommets et inversement. Chaqu'un reste dans son groupe,
les arêtes dans le groupe des arêtes, les sommets dans le groupe des sommets.
[1] 2
Accueil
DMJ: 27/01/2022
