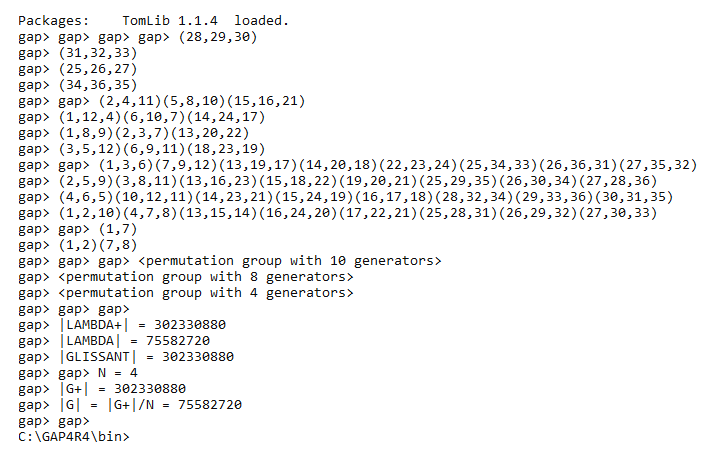
Les secrets du Pyraminx

Schéma de marquage

On commence par fixer le Twist.
Fixer le Twist : B(as)=j(aune), A(vant)=v(ert), G(auche)=o(range), D(roite)=r(rouge)

1. Marquage des facettes

* Sommets : B=0 puis dans le sens horaire 1,-1, A=0 puis dans le sens horaire 1,-1,
* Centres (comme les sommets) : B=0 puis dans le sens horaire 1,-1, A=0 puis dans le sens horaire 1,-1,
* Arêtes : Imaginez d'une part, qu'on a des "emplacements" à 2 facettes marquées comme indique la fig1 ci-dessous

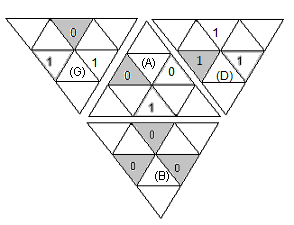fig1	diagramme de marquages

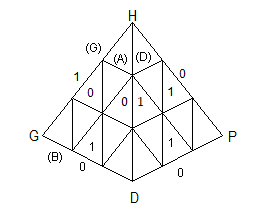
2. Couleur dominante

Les couleurs dominantes : jaune > vert > orange > rouge (les couleurs dont le marquage est zéro 0)
* Les sommets (numérotés) ayant 3 couleurs dont l'une est dominante (couleur marquagée zéro 0).
* Les centres (numérotés) ayant 3 couleurs dont l'une est dominante (couleur marquagée zéro 0).
* Les arêtes (numérotées) ayant 2 couleurs (comme indique la fig2 ) dont l'une est dominante (couleur marquagée zéro 0). .

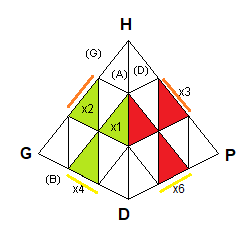sommets, arêtes : numérotés	fig2

Voici les 6 arêtes avec leur couleur dominante en première:
x₁=(vr), x₂=(vo), x₃=(or),
x₄=(jv), x₅=(jo), x₆=(jr)

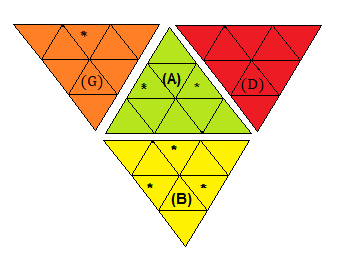Couleur dominante "*"

3. Orientation

* Quand la couleur dominante du sommet y_i se trouve sur une facette marquée 0,1,-1 son orientation vaut 0,1,-1
* Quand la couleur dominante du centre z_i se trouve sur une facette marquée 0,1,-1 son orientation vaut 0,1,-1
* Les arêtes x_i se baladent d'emplacement en emplacement pour se loger dans des emplacements (BA), (GD)..., à chaque fois que la couleur dominante se trouve sur une facette marquée 1 son orientation vaut 1 (1 flip) , sinon elle vaut 0 zéro, par exemple l'arête (vr)=x₁ se place dans (BA) avec vert=B, alors x₁ vaut 0 (0 flip) car la couleur dominante vert est sur la facette marquée 0, de même si l'arête (jo)=x₅ se trouve dans (AG) avec jaune=G, alors x₅ = 1 (1 flip) car la couleur dominante jaune se trouve sur 1 .

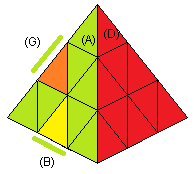x1=0, x5=1

Le groupe du Pyraminx (G,.)

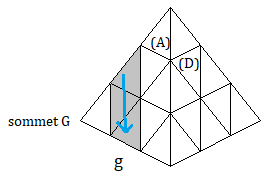rotation G	rotation g

sommets, arêtes : numérotés	sommets, arêtes, centres : numérotés

1¤ M = < G,D,H,P,g,d,h,p >

**Une arête peut balader par tout on a donc affaire à S₆ et une arête a 2 orientations on a donc affaire à Z₂⁶ pour les arêtes on a:
S₆ x Z₂⁶ ,
**Les sommets ne se déplacent pas mais ont 3 orientations , comme on a 4 sommets on a donc affaire à Z₃⁴ .
**Les centres , on peut concidèrer les 3 centres autour d'un sommet comme un gros sommet à 3 orientations , comme on a 4 gros sommets on a donc affaire à Z₃⁴, on pose :

2¤ G⁺ = S₆ x Z₂⁶ x Z₃⁴ x Z₃⁴ ; |G⁺| = 302330880
s = (u,x,y,z) ∈G⁺
u ∈ S₆
x = (x₁, x₂,x₃, x₄,x₅,x₆ ) ∈ Z₂⁶ ,
y = (y₁, y₂,y₃ ,y₄ ) ∈ Z₃⁴ ,
z = (z₁, z₂,z₃ ,z₄ ) ∈ Z₃⁴ ,

* La loi '.' dans G⁺ définie par : (u,x,y,z)(u',x',y',z') = (uu', x+u(x'),y+y',z+z')
uu' = u' o u
u(x) = (x_u(1), x_u(2), ...,x_u(6) ) , u=permutation, x=vecteur

3¤ Action '•' de M sur G⁺ On définit une action '•' de M dans G⁺ ainsi
G⁺ x M --> G⁺
(s,V) --> s•V = t
Vérifiant les axiomes suivants:
A₁ : s•I = s ; élément neutre
A₂ : (s•V)•T = s•(VT) ; associativité
A₃ : a donné,fixé
a•V = a ==> V=I ; librement
A₄ : s•(VT) = (s•V)(s•T) ; compatibilité

¤4 Le groupe G du Pyraminx est par définition :
G = {s∈G⁺ | s=e•V , V∈M}
|G| = 75582720 (donné par GAP)

Les 2 lois du Pyraminx

(F) : Loi des flips: la somme des orientations des arêtes est un nombre pair

∑ x_i = 0 (mod 2) ou en abrégé x = 0 (mod 2) avec x = (x₁,x₂,x₃,...,x₆)
on dit qu'il y a une conservation des flips .

Démonstration :
==> (i) Pour une rotation de base, d par ex et l'état (j,a) associé à d avec
a = (1,0,0,0,0,1) on a bien a=0 (mod 2)
On peut vérifier ainsi que le vecteur d'orientation des autres rotations de base est aussi un multiple de 2.

==> (ii) Soit V≠I Une formule avec l'état (u',x') associé . On peut toujours mettre V sous la forme : V=Td où T (état (u,x)) et une rotation de base par ex d (état (j,a)), il est donc de la forme:
V = Td
d'où
(u',x') = (u,x)(j,a) = (uj,x+u(a))

x' = x + u(a)

On va démontrer la loi par récurrence sur la longueur de la formule.

¤ Pour n=1 , les rotations de base ont tous un vecteur d'orientation un multiplie de 2 d'après (i)
¤ Supposons à l'étape n , formule T , état (u,x) avec x=0 (mod 2) ; Hypothèse de Récurrence
¤ Voyons si à l'étape n+1, formule V , état (u',x') la loi vérifie encore. Or d'après (ii) on a:
V = Td ==> x' = x + u(a)
comme
x = 0 (mod 2) ;HR
et a = 0 (mod 2) ==> u(a) = 0 (mod 2) ,u ne change rien sur le modulo
donc
x' = 0 (mod 2)

la 1ère loi est ainsi démontrée.

(P) : Loi de parité: les permutations des arêtes sont paires

Démonstration : La démonstration se fait en 2 étapes.
A1. Une rotation de base d par exemple, fait permuter 3 arêtes
Soit j = la permutation assiociée à d

On a j = 1->6->4 = (1,6,4) c'est une parmutation paire comme une formule V est composée de rotations de base donc la permutation q associée à une formule V est paire (la somme des nombres pairs est paire)
On a donc montré qu'une formule gènère une permutation paire q ∈ A₆.

A2. Inversement, étant donnée une permutation paire q, il faut trouver une formule V associée.
Pour cela on utilise la propriété suivante:

Propriété : La famille des 3-cyles (a,b,x) où a,b donnés et x ∈ {1,2,3,4,5,6}-{a,b} engendre A₆

En cherchant un peu on trouve les 3-cycles désirés
[hd] => α = (1,4,3)
p[hd]p' => β = (1,4,6)
p'[hd]p => γ = (1,4,5)
[d'g] => δ = (1,4,2)
Donc pour n'importe permutation paire q, elle est exprimée par α,β,γ,δ donc on trouve bien une formule associée à q.
Autrement dit <g,d,h,p> donne exactement A₆

La 2ème loi est ainsi démontrée

REMARQUE
Trouver la famille (a,b,x) où a,b fixes et x ≠ a,b n'est pas évident à trouver à priorie. mais il y a une technique que nous avons déjà utilisée dans la section "MATHSCUBING: Square-1"

Théorème fondamental de la Cubologie :

On démontre le théorème suivant:
G = {s∈G⁺ | s vérifie (F), (P)}

G = A₆ x Z₂⁵ x Z₃⁴ x Z₃⁴ , |G| = 75582720
D'après les lois (F), (P) le nombre de contraintes vaut N = 2.2 = 4
|G| = |G⁺| / N

Comment a-t-on trouvé la loi '.' dans (G⁺, .) ?

Pour les sommets et les centres la loi est simple : y+y', z+z' car on est dans Z₃⁴

Pour les arêtes c'est plus compliqué
On voudrait définir le produit de deux arêtes
(u,x)(u',x') = (w,t)
Comment trouver w et t ?
Pour w on voit facilement que w = uu' , car si on déplace les pièces par u puis par u' , on déplace les pièces bien par uu'.
Pour trouver t c'est plus compliqué ... ça se fait en plusieurs étapes . Allons-y

Loi de composition

On note : e•d = (j,a)
Pour dire que la rotation de base d engendre l'état (j,a) où j=permutation et a=orientation,
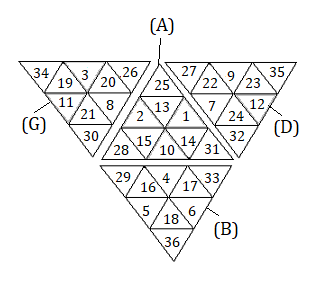
pour trouver j et a, on utilise le diagramme des numérotations et le diagramme des marquages.

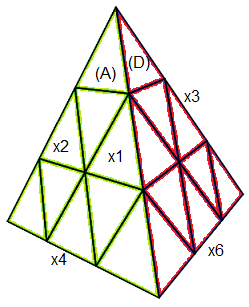diagramme des numérotations	diagramme des numérotations abrégées

On voit que pour la rotation d, j vaut : j = 1->6->4 = (1,6,4)
Pour trouver l'orientation a , on utilise le diagramme de marquage

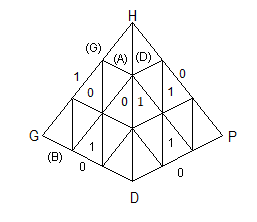diagramme des marquages	vecteur orientation a

et on voit que a = (1,0,0,0,0,1)
finalement on a:
e•d = (j,a) avec
j = (1,6,4)
a = (1,0,0,0,0,1)
Ainsi on peut trouver les étas associés pour les autres rotations g,h,p.

e•g = (j,a)
j = (2,4,5)
a = (0,0,0,1,1,0)

e•h = (j,a)
j = (1,2,3)
a = (1,0,1,0,0,0)

e•p = (j,a)
j = (6,3,5)
a = (0,0,0,0,1,1)

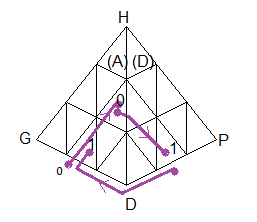
D'après le marquage on a:
(BA)=(x₃,1+x₃), (AD)=(x₂,1+x₂), (BD)=(x₅,1+x₅).
Les x_i sont placés sur la couleur dominante.

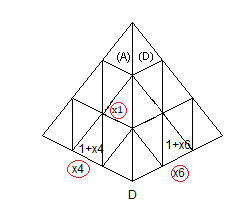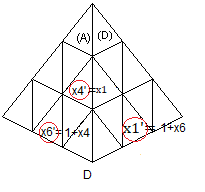Avant la rotation d	Après la rotation d

x'₁ = 1+x₆
x'₄ = x₁
x'₆ = 1+x₄

Or pour la rotation d on a:
Permutation: j = (1,6,4)
Orientation: a = (1,0,0,0,0,1)
on en déduit:
x' = a + j(x)
où j(x) = (x_j(1), x_j(2), ..., x_j(6) )

Chaque formule V (état (u',x')) commence par une rotation de base par ex d (état (j,a)) et le reste T (état (u,x)) on a :
V = dT
(u',x') = (j,a)(u,x) = (ju,a+j(x))
ce qui suggère le produit des 2 arêtes est :
(u,x)(u',x') = (uu',x+u(x'))

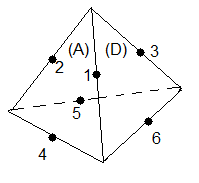
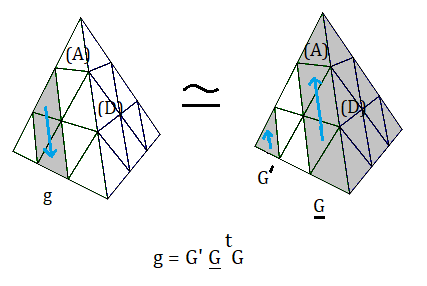
Le groupe Glissant (Slice group) du Pyraminx

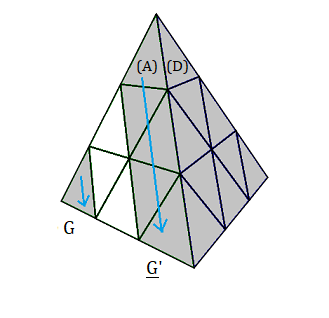rotation g	numérotation des autocollants

On pose :
Q = < g,d,h,p >
Le groupe Glissant S du Pyraminx est par définition :
S = {s∈G⁺ | s=e•V , V∈Q}
|S| = |G⁺| / N.3⁴ (pas de sommets)
|S| = 933120

#gap_pyraminx.txt
#permutations de base :
#permutations sommet
pG := (30,28,29);
pD := (33,31,32);
pH := (27,25,26);
pP := (35,34,36);
#per tranche: (arete)(arete)(centre)
pg := (2,4,11)(8,10,5)(21,15,16);
pd := (1,12,4)(7,6,10)(17,14,24);
ph := (1,8,9)(7,2,3)(22,13,20);
pp := (3,5,12)(9,11,6)(23,19,18);
#permutations étendues (violer les lois)
pGamma := (1,7);
pOmega := (1,2)(7,8);
LAMBDAPLUS := Group( pG, pD, pH, pP, pg, pd, ph, pp, pGamma, pOmega );
LAMBDA := Group( pG, pD, pH, pP, pg, pd, ph, pp);
S := Group( pg, pd, ph, pp);

N := 2*2 ;;
Print( "\n" );
Print( "|LAMBDA+| = ",Size( LAMBDAPLUS ), "\n" );
Print( "|LAMBDA| = ", Size( LAMBDA ) , "\n" );
Print( "|S| = ", Size( S ) , "\n" );
Print( "N = ",N , "\n" );
Print( "|G+| = ", Factorial(6) * (2^6) * (3^4) *(3^4), "\n" );
Print( "|G| = |G+|/N = ", (Factorial(6) * (2^6)*(3^4)*(3^4)) / N, "\n" );

Λ⁺ = < p_G, p_D, p_H, p_P, p_g, p_d, p_h, p_p, p_Γ, p_Ω > ;
Λ = < p_G, p_D, p_H, p_P, p_g, p_d, p_h, p_p > ;
S = < p_g, p_d, p_h, p_p > ;

rotation tranche

[1]

Accueil

DMJ: 03/11/2024