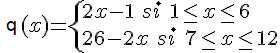Le groupe de Mathieu M₁₂

1- Rappel sur les groupes finis simples

Un groupe simple c'est un groupe qui ne contient pas de sous groupes normaux (à par 1 et G bien sur) , par exemple Z_p avec p = premier, et les A_n avec n ≥ 5
La classification des groupes finis simples s'est terminée en 1983 (légère correction en 2004) , il y a 18 familles et 26 groupes non classables nommés sporadiques . Le groupe M₁₂ est l'un des sporadiques découvert par Mathieu dans les années 1860 (Mathieu en a découvert cinq)

2- Le groupe M₁₂

Le groupe M₁₂ est assez simple à construire
Soit: E = {1,2,3,4,5,6,7,8,9,10,11,12}
Soient p et q, deux fonctions suivantes:

p(x) = 13 - x
et


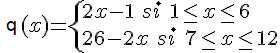
ce qui donne comme permutations:
p = (1,12)(2,11)(3,10)(4,9)(5,8)(6,7)
q = (2,3,5,9,8,10,6,11,4,7,12)
Et M₁₂ c'est l'ensemble des permutations de E engendrées par p et q
M₁₂ = < p, q >
On a: |M₁₂| = 12!/7! = 95040
Remarque : les permutations p et q sont paires donc M₁₂ est un sous groupe de A₁₂

3- Le Rubik's Cube et M₁₂

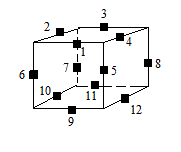
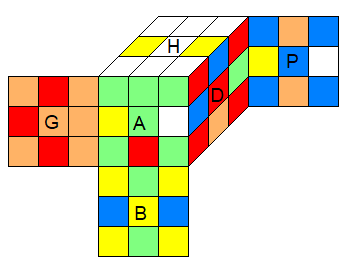
On va noter les arêtes comme indique la fig ci-dessous
(HA)=1,(HG)=2,(HP)=3,(HD)=4
(AD)=5,(AG)=6,(PG)=7,(PD)=8
(BA)=9,(BG)=10,(BP)=11,(BD)=12

1,2,3,4 5,6,7,8 9,10,11,12

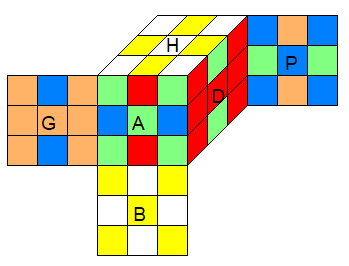
Posons :
C = HP²H²G²D²H²A²H' (14* , *=minimal)
S = BH'G²H' .P²BG² .ADHGH'.A'D'BA'B .H'DBD' (24)
d'où
M₁₂ = < C, S >

e•C = c = (p,0,id,0)

	e•S = s = (q,0,id,0)

Les formules C et S engendrent exactement M₁₂, il est remarquable que le Rubik's Cube contient M₁₂ car c'est un groupe simple sporadique, les groups simples sporadiques il n'y en a que 26.

Une question se pose naturellement: si on mélange le Cube avec C et S comment le restaurer avec seulement C et S ?

[1] 2

Accueil

DMJ: 01/03/2024