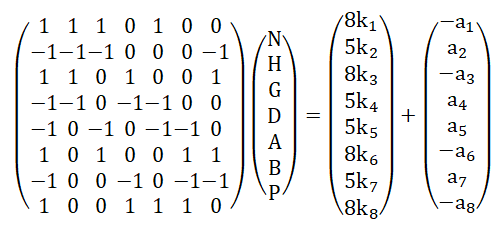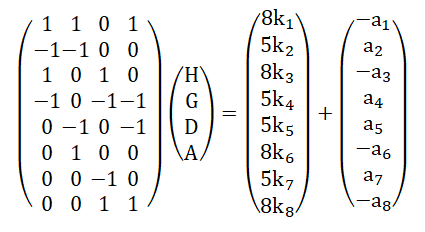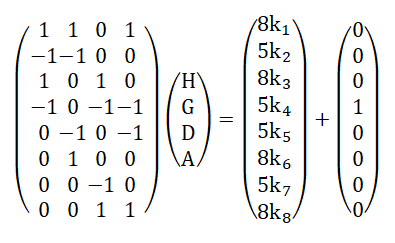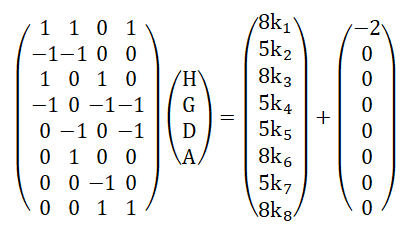La face cachée du Gear Shift
26
Jul
2018
Préface
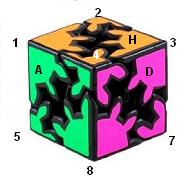
Le Gear Shift ne possède pas des rotations proprement parler, les pièces ne déplacent pas elles restent sur place et pivotent seulement.
Le but de cet article c'est retrouver les formules H-8G8A-8 , H-5D5A-5 qui permettent de résoudre le Gear Shift
Les notations
Les "rotations" du Gear Shift sont assez spéciales.
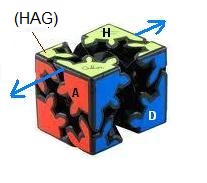
A = Ecarter Avant-Postérieur, puis tourner (HGA) 1 cran dans le sens horaire.
A
-1 = Ecarter Avant-Postérieur, puis tourner (HGA) 1 cran dans le sens contraire
 |
 |
|
rotation A
1.Ecarter Avant-Postérieur
2. Pivoter (HGA) un cran dans le sens horaire |
Equation du type ax+by=c dans Z
Rappelons la résolution de cette équation dans Z
ax + by = c avec (a,b) = 1 (a et b premiers entre eux)
Comme a et b sont premiers entre eux, le théorème de Bezout dit qu'il existe des entiers u,v de Z tels que
au + bv = 1 (A) équation sans seconde membre
Donc soit (x
0, y
0) une solution particulière de (A) , sans seconde membre
On a alors
ax
0 + by
0 = 1
acx
0 + bcy
0 = c
Or on a aussi:
ax + by = c
D'où (en faissant la soutraction)
a(x-cx
0) + b(y-cy
0) = 0
Soit
a(x-cx
0) = b(cy
0 - y) (B)
b|a(x-cx
0) et (a,b)=1 donc
b|(x-cx
0) (théorème de Gauss)
bk = (x-cx
0) (C)
En rapportant dans (B) on trouve
abk = b(cy
0 - y)
Soit
y = cy
0 - ak
et de (C) on tire
x = cx
0 + bk
En résumé les solutions de ax+by=c avec (a,b)=1 sont
x = cx
0 + bk
y = cy
0 - ak
Où k est un entier (le
même k pour x et y) et (x
0, y
0) une solution particulière de ax+by=1
Analyse du puzzle
Le Gear Shift possède deux types de rotations: normal N, sans écarter et A, P, H, B, G, D en écartant le cube.
- Pour la rotation N quand on tourne un sommet les 7 autres tournent aussi: les gros sommets dans un sens et les petits sommets dans l'autre sens.
- Pour la rotation A, par exemple, on écarte le cube dans la direction Avant-Postérieur puis on tourne un sommet Avant les 3 autres sommets Avant tournent aussi, de même les gros sommets
dans un sens, les petits dans l'autre sens
- Quand un gros sommet avance 2 crans par exemple, il peut le faire en plusieurs tours ! c'est à dire 8k+2 et le petit sommet reste invariant mais lui aussi il peut faire plusieurs tour 5m et on a la relation suivante:
8k + 2 = 5m
 |
 |
| 8k + 2 = 5m |
5m + 1 = 8k |
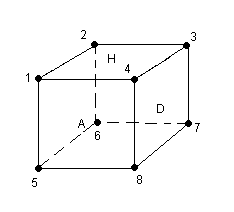
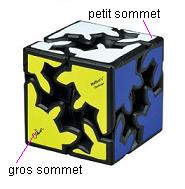
Numéroter les sommets
On numérote les sommets comme indique la fig ci-dessous
Pour le sommet 1, par exemple il peut être pivoté par N , H, G, et A de même pour le sommet 2 il peut être pivoté par N, H, G, et P mais dans l'autre sens... on a donc les relations suivantes:
N + H + G + A + a
1= 8k
1
-N - H - G - P - a
2 = 5k
2
N + H + D + P + a
3 = 8k
3
-N - H - D - A - a
4 = 5k
4
-N - B - G - A - a
5 = 5k
5
N + B + G + P + a
6 = 8k
6
-N - B - D - P - a
7 = 5k
7
N + B + D + A + a
8 = 8k
8
et sous la forme matricielle
V
1, V
2, V
3, V
4, V
5, V
6, V
7
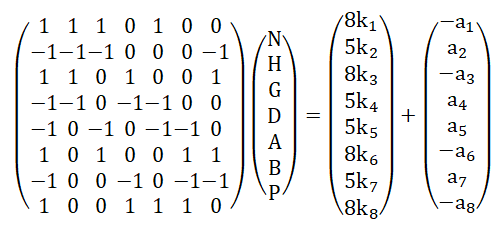
Mais ces 7 vecteurs ne sont pas tous indépendants, en effet on a:
V
1 = V
5+V
7 = V
2+V
6 = V
4+V
3
ou encore
V
1 = V
4+V
3
V
6 = V
4+V
3-V
2
V
7 = V
4+V
3-V
5
Donc on peut enlever V
1, V
6,V
7 et ne garde que V
2,V
3, V
4,V
5 on peut noter que la famille {V
2,V
3, V
4,V
5 }
est libre
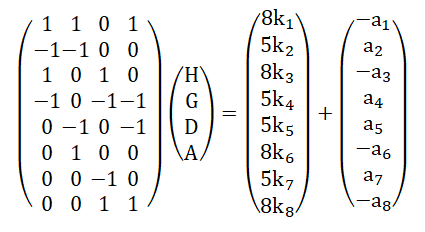
Retrouver la formule H-8G8A-8 = (HDA)1+
Le but de ce paragraphe c'est de retrouver cette formule, Supposons que le sommet 4 avance d'un cran, alors on a le système suivant:
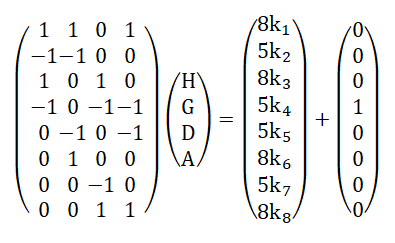
On a:
G = 8k
6
D = -5k
7
D + A = 8k
8
- H - D - A = 5k
4+1
D'où
A = 8k
8+5k
7
et
H + 5k
4 = - D - A - 1
H + 5k
4 = -8k
8 - 1
Une solution particulière sans seconde membre est: H=6, k
4=-1 d'où les solutions sont
H = -48k
8 - 6 + 5m
k
4 = 8k
8 + 1 - m
D'où les solutions du système sont (elles dépendent de 4 paramètres indépendantes)
G = 8k
6
D = -5k
7
A = 8k
8+5k
7
H = -48k
8 - 6 + 5m
Si on prend
k
6 = 1 => G = 8
k
7 = 0 => D = 0
k
8 = -1 => A = -8
m = -10 => H = -8
On retrouve la formule
(HDA)
1+ = H
-8G
8A
-8
Note : Si le sommet 4 recule d'un cran on trouvera: (HDA)
1- = H
8G
-8A
8
Retrouver la formule (HGA)2+ = H-5D5A-5
Le but de ce paragraphe c'est de retrouver cette formule, Supposons que le sommet 1 avance de 2 crans, alors on a le système suivant:
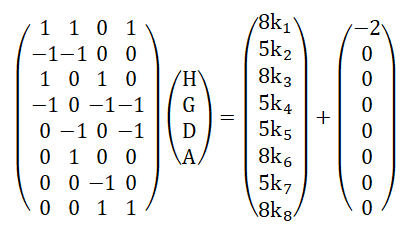
On a:
G = 8k
6
D = -5k
7
H + G = -5k
2
H + G + A = 8k
1-2
D'où
H + 5k
2 = -8k
6
Une solution particulière sans seconde membre est: H=6, k
2=-1 d'où les solutions sont
H = -48k
6 + 5m
k
2 = 8k
6 - m
De même pour
A - 8k
1 = -2 + 40k
6 - 5m
Une solution particulière sans seconde membre est: A=9, k
1=1 d'où les solutions sont
A = -18 + 360k
6 - 45m -8p
k
1 = -2 + 40k
6 - 5m -p
D'où les solutions du système sont (elles dépendent de 4 paramètres indépendantes)
G = 8k
6
D = -5k
7
H = -48k
6 + 5m
A = -18 + 360k
6 - 45m -8p
Si on prend
k
6 = 0 => G = 0
k
7 = -1 => D = 5
m = -1 => H = -5
p = 4 => A = -5
On retrouve la formule
(HGA)
2+ = H
-5D
5A
-5
Note : Si le sommet 1 recule de 2 crans on trouvera: (HGA)
2- = H
5D
-5A
5
[1] 2
Accueil
DMJ: 26/07/2018