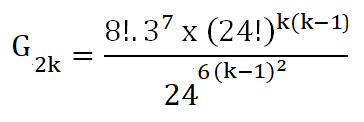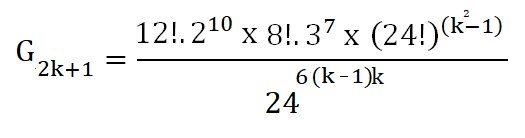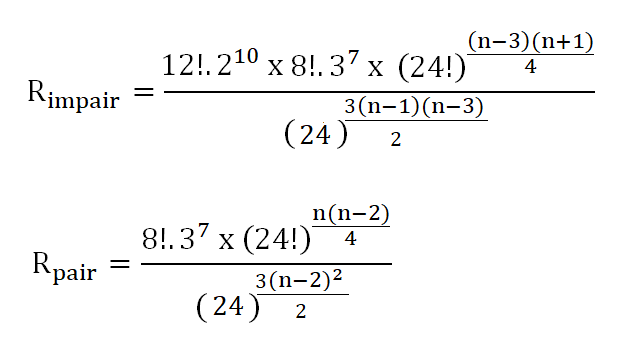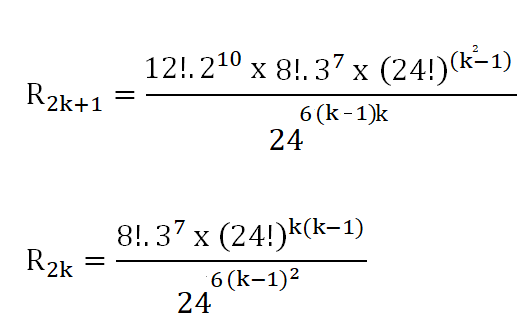Le nombre d'états du Rubik n³

Observation

Ce qui est important c'est de savoir combien type de pièces dans ce genre de puzzle, et que dans chaque type il y a combien de familles ? (de clans, d'orbites). On a 2 cas : n est pair ou impair.

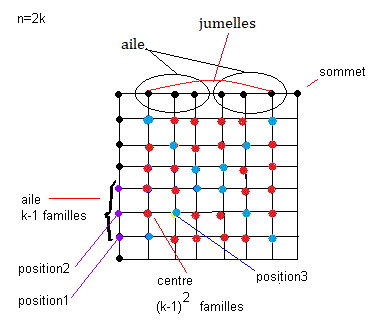
Cas pair: n = 2k

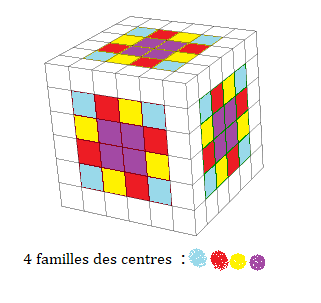
Pour fixer les idées on va choisir n = 8
Observons bien, il y a plusieurs type de pièces dans ce puzzle, et pour chaque type il y a plusieurs familles (clans, orbites,...)

Les familles des centres

Les sommets :
Il y a 8 sommets qui peuvent balader partout donc
8 ---> 8!
et chaque sommet a 3 orientations ---> 3⁸
finalement ---> 8!.3⁸ (une seule famille)

Les ailes :
Il y a plusieurs familles d' ailes, en effet les ailes en position 1 ne peuvent pas aller en position 2, toutes les ailes en position 1 forment ainsi une famille (un clan, une orbite,...) . Il y a plus précisement (k-1) familles d'ailes
dans chaque famille il y a évidemment 24 ailes (4 par faces et on a 6 faces), ces ailes peuvent balader partout donc: 24 ---> 24!
Comme il y a (k-1) familles on a :
finalement ---> (24!)^(k-1)

Les centres :
Il y a plusieurs familles de centres (même raisonnement comme pour les ailes) , le calcul du nombre de familles est assez simple: On somme les nombres 1+3+5, ..... à une longueur (k-1) (voir fig), donc
1+3+5+ ... ;(longueur k-1)
= (k-1)² familles de centres ==> (k-1) familles centre-diag C_i, (k-1)(k-2) familles centre-aile C_ij,
Dans chaque famille il y a 24 centres (4 par faces et on a 6 faces) 24 ---> 24! et on a (k-1)² familles .
finalement ---> (24!)^(k-1)²

ce qui donne:
G⁺ = 8! .3⁸ x (24!)^(k-1) x (24!)^(k-1)²
G⁺ = 8! .3⁸ x (24!)^(k-1)k
Mais on ne peut pas atteindre tous ces configurations, car il y a des contraintes , provenant du core .

NOTATION :
S = permutation sommet, s_i = vect orientation sommet
C_i = permutation centre-diag-i
C_ij = permutation centre-aile-ij
W_i = permutation aile-i

Contraintes :
1) Σ s_i = 0 (mod 3) ===> 3
2) sig(C_i) = sig(S) ===> 2^k-1 .2¹/2 = 2^k-1
3) sig(C_ij) = sig(S).sig(W_i).sig(W_j) ; pour sig(C_ij), on a: 2 valeurs et (k-1)(k-2) familles ===> 2^(k-1)(k-2)

soit le nombre de contraintes N :
N = 3 .2^k-1 .2^(k-1)(k-2)

Pour une famille on a :
4 centres
balader partout ---> 4!
6 faces ---> 4!⁶
permutation doit etre paire --> 4!⁶/2
comme on a (k-1)² familles d'où le nombre de permutations des centres est:
C = (4!⁶/2)^(k-1)²

G^# = G⁺ / N = 8! .3⁷ x (24!)^(k-1)k / 2^(k-1)²
d'où le nombre d'états G :
G = G^# / C



Ce qui est étonnant c'est que dans le cas pair, il n'y a plus d'arêtes !! , il n'y a que des ailes (pas d'orientations)!

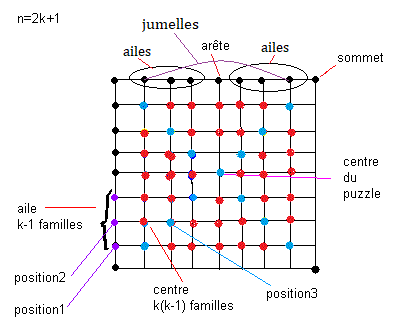
Cas impair: n = 2k + 1

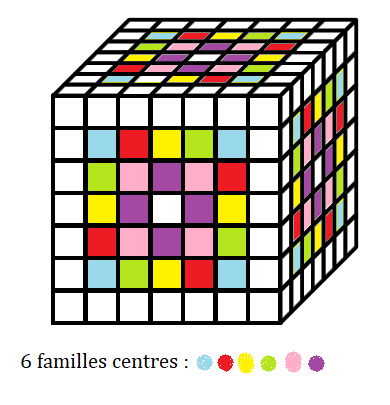
Pour fixer les idées on va choisir n = 9
Observons bien, il y a plusieurs type de pièces dans ce puzzle, et pour chaque type il y a plusieurs familles (clans, orbites,...)

Les familles des centres

Les arêtes :
Il y a 12 arêtes qui peuvent balader partout donc
12 ---> 12!
et chaqu'arête a 2 orientations ---> 2¹²
finalement ---> 12! .2¹² (une seule famille)

Les sommets :
Il y a 8 sommets qui peuvent balader partout donc
8 ---> 8!
et chaque sommet a 3 orientations ---> 3⁸
finalement ---> 8! .3⁸ (une seule famille)

Les ailes :
Il y a plusieurs familles d' ailes, en effet les ailes en position 1 ne peuvent pas aller en position 2, toutes les ailes en position 1 forment ainsi une famille (un clan, une orbite,...) . Il y a plus précisement (k-1) familles d'ailes
Dans chaque famille il y a évidemment 24 ailes (4 par faces et on a 6 faces), ces ailes peuvent balader partout donc: 24 ---> 24!
Comme il y a (k-1) famille on a:
finalement ---> (24!)^(k-1)

Les centres :
Il y a plusieurs familles de centres (même raisonnement comme pour les ailes) , le calcul du nombre de familles est assez simple: On somme les nombres 2+4+6, ..... à une longueur (k-1) (voir fig), donc
2+4+6+ ... ; (longueur k-1)
= 2+4+6 ... +2(k-1)
= 2(1+2+3 ...+(k-1))
= 2(k-1)k/2
= (k-1)k familles de centres ==> (k-1) familles centre-diag C_i, (k-1)² familles centre-aile C_ij,
Dans chaque famille il y a 24 centres (4 par faces et on a 6 faces) 24 ---> 24! et on a (k-1)k familles .
finalement ---> (24!)^(k-1)k

ce qui donne:
G⁺ = 12! .2¹² x 8! .3⁸ x (24!)^(k-1) x (24!)^(k-1)k
G⁺ = 12! .2¹² x 8! .3⁸ x (24!)^(k²-1)
Mais on ne peut pas atteindre tous ces configurations , car il y a des contraintes , provenant du core .

NOTATION :
S = permutation sommet, s_i = vect orientation sommet
A = permutation arête, a_i = vect orientation arête
C_i = permutation centre-diag-i
C_ij = permutation centre-aile-ij
W_i = permutation aile-i

Contraintes :
1) Σ a_i = 0 (mod 2) ===> 2
2) Σ s_i = 0 (mod 3) ===> 3
3) sig(C_i) = sig(S) = sig(A) ===> 2^k-1.2¹.2¹/2 = 2^k
4) sig(C_ij) = sig(S).sig(W_i).sig(W_j) ; pour sig(C_ij), on a: 2 valeurs et (k-1)² familles ===> 2^(k-1)²

soit le nomnre de contraintes N:
N = 2 .3 .2 .2^k-1 .2^(k-1)²

Pour une famille on a :
4 centres
balader partout ---> 4!
6 faces ---> 4!⁶
permutation doit etre paire --> 4!⁶/2
comme on a (k-1)k familles d'où le nombre de permutations des centres est:
C = (4!⁶/2)^(k-1)k

G^# = G⁺ / N = 12! .2¹⁰ x 8! .3⁷ x (24!)^(k²-1)/2^(k-1)k
d'où le nombre d'états G :
G = G^# / C


En résumé: Voici le nombre d'états pour un Rubik's Cube de dimension n:

1 [2] 3 4 5 6

Accueil

DMJ: 14/08/2024