Le groupe de Skewb

Orientation des sommets
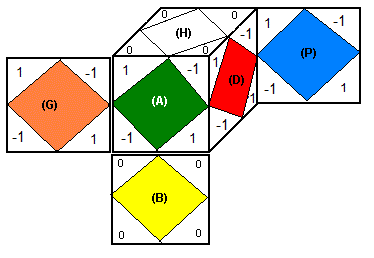
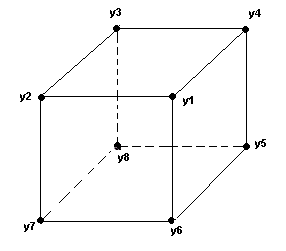
Comme pour le Rubik's Cube, on oriente des sommets comme indique la fig5, on numérote les sommets (fig6) de telle façon qu'on puisse regrouper les sommets pairs et impairs. Les sommets ont 3 couleurs dont l'une est dominante.

fig5 : orientation	fig6 : numérotation des sommets (pour pair et impair)

On prend un Skewb standard:
H(aut)=b(lanc), B(as)=j(aune), A(vant)=v(ert), P(ostérieur)=k(lein), G(auche)=o(range), D(roite)=r(ouge)
Voici les couleurs dominantes pour les sommets:
blanc et jaune sont des couleurs dominantes

y₁=(brv), y₂=(bvo), y₃=(bok), y₄=(bkr)
y₅=(jrk), y₆=(jvr), y₇=(jov), y₈=(jko),

Les sommets y_i se baladent pour se placer dans des emplacements-sommets, à chaque fois que la couleur dominante se trouve sur une facette marquée 1 son orientation vaut 1 (1 twist) , sur -1 son orientation vaut -1 (-1 twist) , sur 0 son orientation vaut zéro (0 twist, bien orienté). par exemple le sommet y₅=(jrk) se place en (HDA) avec jaune=D, alors y₅ vaut 1 (1 twist) car la couleur dominante jaune est sur la facette 1, de même pour le sommet y₂ = (bvo) dans (BAD) avec blanc=D alors y₂ = -1 (-1 twist) car la couleur dominante blanc se trouve sur -1 .

L'orientation des sommets pour le Skewb est beaucoup plus difficile à comprendre que chez le Rubik's Cube

On a 2 groupes de sommets ceux qui sont attachés au core (les Pairs) et ceux qui sont libres (les Impairs), les pièces se déplacent chacun dans leur camp.
On nomme les sommets libres ℑ = {A,P,E,O} = {y₁,y₃,y₅,y₇} les sommets Impairs et les sommets liés ℘ = {G,D,B,H} = {y₂,y₄,y₆,y₈} les sommets Pairs .
Les Impairs déplacent les Pairs et inversement.
Les mouvements des sommets peuvent se faire de deux façons:
Pairs déplacent Impairs :
-permutations de type (a,b,c) provenant des rotations de base
-permutations du type (a,b)(c,d) provenant des commutateurs

Quand le déplacement est réalisé par (a,b,c), le camp déplaçant (Pairs) gagne 1, ou -1 twists et le camp déplacé (Impairs) gagne -3, ou 3 twists
en effet
pour fixer des idées on prend par ex la rotation G, qui déplace P,A,O et le camp ℘ gagne 1 et ℑ gagne -3 ( -3=6 (mod 3) )

Quand le déplacement est réalisé par (a,b)(c,d), le camp déplaçant gagne 0 twists et le camp déplacé 3, ou -3
en effet
(a,b)(c,d)=[X,Y]=XYX'Y' ceci apport 0 pour le camp déplaçant et 3,-3 pour le camp déolacé

Les pièces déplacées apportent à leur groupe un nombre 3k d'orientations (un multiple de 3)

En résumé: si les sommets-Pairs ℘ déplacent les sommets-Impairs ℑ alors ℑ gagne 3k twists, et le nombre de twists de ℘ varie

Voici les questions:
Q1: La loi des twists est elle vérifiée: ∑ y_i = 0 (mod 3) ?
R1: Non , car les permutations (a,b,c) modifie le nombre de twists.

Q2: Pourquoi , quand les sommets sont isolés la loi des twists s'applique: ∑ y_i = 0 (mod 3) ?
R2: Parce que quand les sommets sont isolés, les déplacements se font par (a,b)(c,d) on a: 0 twists pour le camp déplaçant et 3k le camp déplacé

La loi des twists: conservation des twists
Quand les déplacements se font uniquement par des commutateurs, alors on a la loi des twists :
* La somme des orientations des sommets-Impairs est un multiple de 3
∑ y_2i+1 = 0 (mod 3)
* La somme des orientations des sommets-Pairs est un multiple de 3
∑ y_2i = 0 (mod 3)

En effet dans ces conditions:
les déplacements apportent 0 twists au camp déplaçant et 3k au camp déplacé
Il résulte que la somme des orientations des sommets est un multiple de 3
∑ y_i = 0 (mod 3)

on dit qu'il y a une conservation des twists .

En particulier quand les sommets sont "isolés" (les sommets haut sont en Haut, les sommets bas sont en Bas) on a la loi des twists
Parce que les déplacements se font par (a,b)(c,d)

Comparons
Rubik's Cube: ∑ sommets = 0 (mod 3)
Skewwb: Quand les sommets sont isolés :
* ∑ sommets-Impairs = 0 (mod 3)
* ∑ sommets-Pairs = 0 (mod 3)

I. Analyse
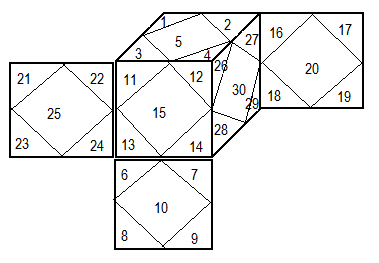
On numérote les stickers ainsi :

stickers numérotés

Un élément de G est une configuration des autocollants, donc G est un sous-groupe de S₃₀ (30 stickers ) en effet l'autocollant 11 ne vient pas en 5, de même l'autocollant 4 et 12 ne peuvent pas échanger celà signifie que les permutations (11,5,...) et (4,12) ne font pas parties de G, G ne contient pas toutes les permutations de S₃₀ . Voyons G de plus prés. On a remarqué que les sommets ne se mettent jamais à la place d'un centre et inversement. Les 8 sommets se permutent entre eux, de même pour les centres, et chaque sommet a 3 orientations donc on a affaire à:
pour les sommets c'est: S₈ x Z₃ ⁸
pour les centres c'est: S₆
finalement G se trouve dans un truc composé de 3 "morceaux"

G ⊂ G_* = S₈ x Z₃⁸ x S₆

II. Analyse
Si on remarque bien, les sommets-Pairs (les y_2i) déplacent les sommets-Impairs (les y_2i+1), et inversement. on a donc 2 clans de sommets, ceux qui déplacent des sommets-Impairs (les Pairs) et ceux qui déplacent les sommets-Pairs (les Impairs)
finalement G_* = S₈ x Z₃⁸ est scindé en 2 morceaux:
G⁺ = (S₄ x Z₃⁴) x (S₄ x Z₃⁴)
d'où
G ⊂ G⁺ = S₄ x Z₃⁴ x S₄ x Z₃⁴ x S₆

III. Analyse
Une rotation de base, déplace 3 sommets (resp. 3 centres) en un 3-cycle, donc les permutations des sommets (resp. des centres) sont des permutations pairs, on a donc
A₄ à la place de S ₄ (resp. A₆ à la place de S ₆ ) donc
G ⊂ A₄ x Z₃⁴ x A₄ x Z₃⁴ x A₆

IV. Analyse (plus délicate)
C'est le passage de Z₃⁴ à Z₃³ qui est délicate. En effect, quand les 4 sommets-Pairs sont bien placés, alors le 4ième est forcement bien orienté, car la loi:
∑ y_2i = 0 (mod 3) oblige le 4ième soit bien orienté. Même raisonnement pour les sommets-Impairs
pour l'orientation, on a seulement besoin Z₃³ au lieu de Z₃⁴

finalement G est exactement:

G = A₄ x Z₃³ x A₄ x Z₃³ x A₆

==> Ceci nous montre que le Skewb a 2 lois de twists:
* ∑ sommets-Impairs = 0 (mod 3)
* ∑ sommets-Pairs = 0 (mod 3)
==> Ceci nous montre que le Skewb a 3 lois de parité:
sig(sommets-Impairs) = 1
sig(sommets-Pairs) = 1
sig(centres) = 1
d'où le nombre de contraintes (nombre de choix, nombre d'orbites)
N = 3.3.2.2.2

Q4: Pourquoi quand les sommets haut sont bien placés alors les sommets bas sont automatiquement bien placés ?
R4: Quand les sommets haut sont bien placés ça signifie que A,P sont bien placés donc automatiquement les sommets E,O sont bien placés sinon on aura une permutation impaire (E,O) ce qui est impossible car on est dans A₄ il n'y a que des permutation paires
de même quand les sommets haut sont bien placés ça signifie que G,D sont bien placés donc automatiquement les sommets B,H sont bien placés sinon on aura une permutation impaire (B,H) ce qui est impossible car on est dans A₄ que des permutation paires
finalement A,P,G,D bien placés => E,O,B,H bien placés

Rappel produit de 2 configurations :
(v,y,s,t,w), (v',y',s',t',w') ∈ (S₄ x Z₃⁴) x (S₄ x Z₃⁴) x S₆
(v,y,s,t,w)(v',y',s',t',w') = (vv', y + v(y'),ss',t+s(t'), ww')
vv' = v' o v
p(x) = (x_p(1), x_p(2), ..., x_p(n)) , p=permutation, x=vecteur

G = A₄ x Z₃³ x A₄ x Z₃³ x A₆

Et et ......hup làààà

|G| = |G⁺| / N
|G| = 4! 3⁴ x 4! 3⁴ x 6! /3.3.2.2.2 = 37 791 360

G⁺ , le groupe des configurations
Dans G⁺ les pièces se déplacent et pivotent librement (mais chaqu'une dans leur camp) c'est comme s'il n'y a pas de core. ) vaut:
G⁺ = (S₄ x Z₃⁴) x (S₄ x Z₃⁴) x S₆
|G⁺| = 2 720 977 920

Le GAP
Télécharger le GAP .::ICI::. https://www.gap-system.org/Releases/index.html
Dans la fenêtre de cmd on se place dans le dossier de GAP
C:\Users\nom> cd\gap4r4\bin
C:\gap4r4\bin>gap < gap_skewb.txt
ou bien
gap>
Ici on colle le text gap_skewb.txt.

gap_skewb.txt:

pH := (1,13,29)(21,6,18)(17,24,9)(8,19,23)(20,25,10);
pB := (13,26,9)(6,12,29)(24,4,18)(14,28,7)(15,30,10);
pA := (3,27,14)(11,2,28)(22,16,7)(4,26,12)(5,30,15);
pP := (2,22,19)(16,3,23)(27,11,8)(1,21,17)(5,25,20);
pG := (1,12,24)(21,4,13)(17,26,6)(3,11,22)(5,15,25);
pD := (4,17,29)(26,1,18)(12,21,9)(2,16,27)(5,20,30);
pO := (3,28,19)(11,7,23)(22,14,8)(13,6,24)(15,10,25);
pE := (14,2,23)(28,16,8)(7,27,19)(29,18,9)(30,20,10);
pPsi1 := (4,26,12) ;
pPsi2 := (3,11,22) ;
pOmega1 := (3,2)(16,11)(27,22) ;
pOmega2 := (1,4)(21,26)(17,12) ;
pOmega3 := (5,15) ;
Lambdaplus := Group( pH, pB, pA, pP, pG, pD, pO, pE, pPsi1, pPsi2, pOmega1, pOmega2, pOmega3 );
# SLambdaplus := Size( Lambdaplus );
Lambda1 := Group( pH, pB, pA, pP, pG, pD, pO, pE );
# SLambda := Size( Lambda1 );
Print( "\n" );
Print( "|G*| = ", Factorial(8) * 3^8 *Factorial(6) , "\n" );
Print( "|Lambda+| = ",Size( Lambdaplus ) , "\n" );
Print( "|Lambda| = ", Size( Lambda1 ) , "\n" );
Print( "N = ", 2^3 * 3^2 , "\n" );
Print( "|G+| = ", Factorial(4) * 3^4 * Factorial(4) * 3^4 *Factorial(6) , "\n" );
Print( "|G| = |G+|/N = ", Factorial(4) * 3^4 * Factorial(4) * 3^4 *Factorial(6) /(2^3 * 3^2) , "\n" );

Le GAP nous donne bien :
|Λ⁺| = |G⁺| = 2 720 977 920 et
|Λ| = |G| = 37 791 360

Super Skewb
Un Super Skewb (Skewb Uktimate, Golden Cube ...) est un Skewb dont les centres sont orientés.
Orientation des centres

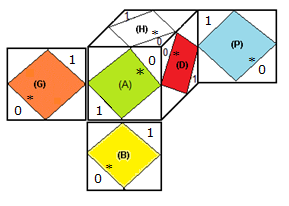centres orientés suivant (HDA) et son antipode (BPG)

Loi des centres:
Quand on pivote les centres sans toucher les sommets,
la somme des orientations des centres = un multiple de 2 (1=180°)
Ce qui donne à l'état résolu on a:
* Soit 2 centres à pivoter, 180° chaqu'un
* Soit 4 centres à pivoter, 180° chaqu'un
* Soit 6 centres à pivoter, 180° chaqu'un

G_s⁺ = (S₄ x Z₃⁴) x (S₄ x Z₃⁴) x (S₆ x Z₂⁶)
G_s = A₄ x Z₃³ x A₄ x Z₃³ x A₆ x Z₂⁵ = 1 209 323 520

Commentaire

La loi des twists est valable seulement pour des mouvements qui conservent le camp, c'est-à-dire les permutations du type (a,b)(c,d) c'est un élément du groupe K=Klein un sous groupe de A₄ par ex pour ℘
K = {id, (G,D)(B,H), (G,B)(H,D), (G,H)(B,D) }

[1]

Accueil

DMJ: 13/01/2024