Les formules premières

Une remarque

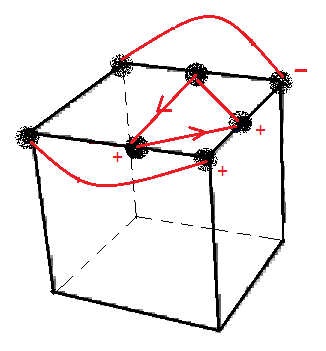
Quand on écrit
A[DH]A' = (HP)->(HA)->(HD) ou A[DH]A' = (HP,HA,HD) on voit que les pièces se déplacent mais on ne voit pas qu'elles se pivotent ! il faut donc trouver une notation qu'on voit aussi les pièces se pivotent en déplacant. Si on écrit
A[DH]A' = (HP)->(HA)⁺->(HD)⁺ ou plus simple A[DH]A' = (HP,HA⁺,HD⁺) là on voit que (HA) et (HD) pivotent (le contenu de (HA) et (HP) pivotent) (note on a: (HA)⁺ = (HA)^- = (HA)°)

de même pour les sommets

A[DH]A' = (HGP)<->(HPD) . (HAG)<->(HDA) ou plus simple A[DH]A' = (HGP,HPD)(HAG,HDA) n'est pas précis, on ne voit pas les sommets pivotent, comme pour les arêtes on écrit
A[DH]A' = (HGP)<->(HPD)^- . (HAG)<->(HDA)⁺ ou plus simple A[HD]A' = (HGP,HPD^-)(HAG,HDA⁺) là , on voit le sommet (HPD) pivote dans le sens anti-horaire et (HDA) pivote dans le sens horaire

Finalement la notation
A[DH]A' = (HP,HA⁺,HD⁺) (HGP,HPD^-)(HAG,HDA⁺) sera beaucoup plus précise, elle décrit exactement l'état du Cube. Si on n'a pas besoin de l'orientation mais simplement les déplacements on écrira
A[DH]A' = (HP,HA,HD)(HGP,HPD)(HAG,HDA) comme d'habitude

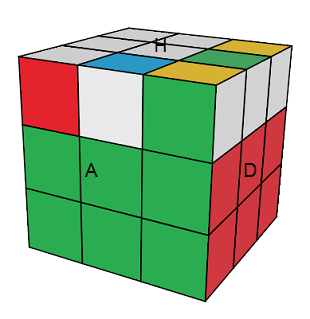
A[DH]A' = (HP,HA+,HD+) (HGP,HPD-)(HAG,HDA+)	A[DH]A'

Formule première

Définition : On dit qu'une formule F est première si elle peut restaurer le Cube.
Par exemple J est première car on peut restaurer le Cube avec seulement J.

1. (HG)<->(HP) = J
2. (HGP)<->(HDA) = J
3. (HG)⁺(HP)⁺ = J²
4. (HGP)⁺(HAG)⁺(HDA)⁺ = J⁴

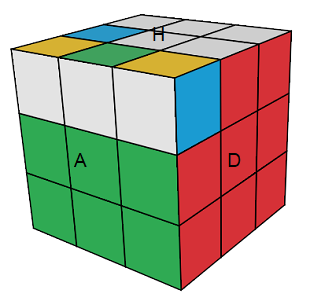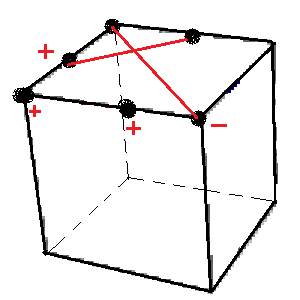J = A[DH]A'.H	J = A[DH]A'.H

Il est donc naturel de se demander s'il existe d'autres types de formules du même genre ? et quelles sont les plus courtes ?

Analyse de J

Rappelle J = A[DH]A'H . Nous allons examiner minutieusement J et essayer de comprendre sa structure, comment se fait-il qu'elle peut restaurer le Cube à elle toute seule.

[1]- J permute un couple d'arêtes (HG)⁺<->(HP) ou plus simple (HG⁺,HP) celà permet de placer toutes les arêtes.

[2]- En permutant elle pivote l'une des arêtes (HG)⁺, mais elle pivote aussi une autre arête (HA)⁺ extérieure de la permutation (la loi des flips est bien vérifiée)
- Si on regarde de plus près , tout celà permet de pivoter un couple d'arêtes, en effet :
J² : (HG),(HP),(HA) ==> (HP)⁺,(HG),(HA)⁺ ==> (HG)⁺,(HP)⁺,(HA)
donc J² pivote bien le couple d'arêtes (HG),(HP)

- si J pivote 2 arêtes en les permutant, ça ne va pas marcher, on ne peut pas pivoter les arêtes, en effet
si J = (HG⁺,HP⁺) => J² = (HG,HP) on ne pivote pas !!
- si J pivote 2 arêtes extérieures de la permutation, ça ne va pas marcher non plus, en effet
si J = (HG,HP)(HA)⁺(HD)⁺ (par ex) => J² = (HG,HP) on ne pivote rien !!

Il y a un seul cas qui marche c'est quand J pivote une arête dans la permutation et une autre arête à l'exterieure de la permutation
J = (HG⁺,HP)(HA)⁺

[3]- Pour les sommets tout se passe exactement comme les arêtes
- J permute 2 sommets en pivotant l'un d'eux (HGP,HDA^-), et elle pivote aussi un autre sommet (HAG)⁺ à exterieur de la permutation

finalement J est de type
J = (HG⁺,HP)(HA)⁺(HGP,HDA^-)(HAG)⁺

D'autres types

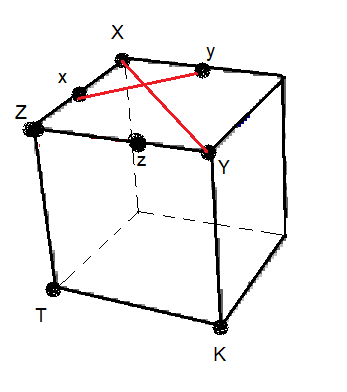
Pour ne pas alourdir les notations on va noter:
x,y,z minuscule les 3 arêtes
X,Y,Z,K,T majuscule les 5 sommets



Analyse
I. Pour pouvoir déplacer, et pivoter toutes les arêtes d'après ce qui est dit plus haut on doit avoir (x⁺,y)z⁺ en effet (x,y) permet de déplacer toutes les arêtes car toute permutation est décomposée en transpositions. Et la loi de parité du Rubik's Cube impose qu'on doit aussi permuter deux sommets (X,Y) c'est-à-dire on doit avoir: (x⁺,y)z⁺(X,Y)

II. La loi des twists impose que pour pivoter les sommets on a:
(X,Y)Z⁺K^-
(X,Y)Z⁺K⁺T⁺
(X,Y)Z^-K^-T^-
(X⁺,Y)Z^-
(X⁺,Y)Z⁺K⁺
etc ...
et on prend seulement les F⁴ pivotent les sommets


Voici les types

N = (x⁺,y)z⁺(X,Y)Z⁺K^-
N⁺ = (x⁺,y)z⁺(X,Y)Z⁺K⁺T⁺
N^- = (x⁺,y)z⁺(X,Y)Z^-K^-T^-

J = (x⁺,y)z⁺(X,Y^-)Z⁺
J = (x⁺,y)z⁺(X,Y⁺)Z^- ; l'anti-J
J⁺ = (x⁺,y)z⁺(X,Y⁺)Z⁺K⁺
J^- = (x⁺,y)z⁺(X,Y^-)Z^-K^-

Δ⁺ = (x⁺,y)z⁺(X⁺,Y⁺)Z⁺
Δ^- = (x⁺,y)z⁺(X^-,Y^-)Z^-

Il y a donc 9 types de formules premières divisées en 3 groupes, et d'après Cube Explorer θ a la longueur minimale 7, |θ|=7, et les autres ont une longueur plus grande

N = H' D H D² A' G' A' G B' P' G P A' B D A' ; |N|=17
N⁺ = D² P' B P' G' B' P' D' A D H P' D' H A' H D' H' ; |N⁺|=19
N^- = A' D A B P' B G P' H G' P' H' D P' D' B² ; |N^-|=17

J = A D H D' H' A' H ; |J|=7
J = D A' H G' A D' A' G H' A² D A' H' D' H² ; |J|=17
J⁺ = H G H' D P' H A H' P H² A' H' G' D' ; |J⁺|=15
J^- = H' D² P H P² B' P H' P' B D' P D' H² ; |J⁺|=17

Δ⁺ = A H A' H' D' H G' H' D P' H' P G ; |Δ⁺|=13
Δ^- = P² D B' D' H' D H P H' P' B D' P² ; |Δ^-|=15

NOTE : l'algorithme minimal est donc

• (x,y) = V
• (X,Y) = V
• x⁺y⁺ = V²
• XⁱY^jZ^k = V⁴

où V est une formule première , x,y arêtes , X,Y,Z sommets et i+j+k = 0 (mod 3)

NOTE : Il existe d'autres formules premières de longueur 7
C = D'[A'H']DH' , bien , c'est le symétrique de J (une A-formule)
O = A[HD]A'H' , (une P-formule)

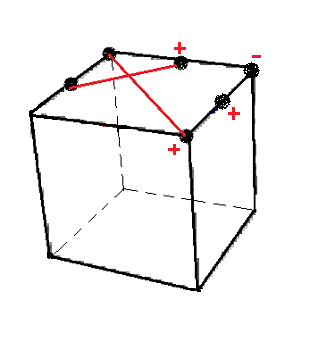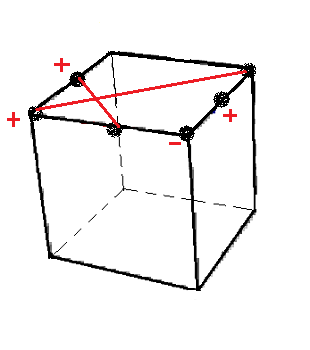C = D'[A'H']DH'	O = A[HD]A'H'

1 2 3 4 5 [6]

Accueil

DMJ: 09/05/2023