La conjugaison

Principe de conjugaison

Le Principe De Conjugaison (PC) stipule que si on peut faire quelque chose à un point alors on peut le faire en tout point ! On va prendre un ex pour bien comprendre. Voici une formule

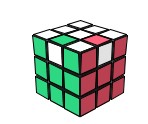
V = AH²A².B'[H'G']B.A²H'A'H'

qui pivote deux arêtes (HA) et (HD) et laisse intactes les autres pièces du Cube (on dira que le reste du Cube est invariant) donc d'après le PC on peut pivoter toutes les arêtes ! par ex si on veut pivoter (AD) et (HP) comment faire ?
Eh bien c'est très simple, il suffit d'ammener (AD) en (HA) et (HP) en (HD) puis apliquer la formule ensuite remettre les arêtes (AD) et (HD) dans leur emplacement initial c'est tout !!
voyons de plus prés:

1. (AD,HA)(HP,HD) = A'P'D'
2. Appliquer la formule: V
3. Remettre les pièces (AD) et (HP) dans leur emplacement initial: DPA

Autrement dit pour pivoter (AD) et (HP) on fait:
(AD)°(HP)° = (A'P'D') .(AH²A².B'[H'G']B.A²H'A'H') .(DPA)
Ainsi on peut utiliser V (avec ses conjugaisons) pour pivoter toutes les arêtes.

NOTE : Par abuse de language on dit que V pivote toutes les arêtes.

V = AH²A².B'[H'G']B.A²H'A'H'	(AD)°(HP)° = (A'P'D')V(DPA)

Le PC s'écrit toujours dans le format : XYX' comme vous avez remarqué sur l'exemple ci-dessus (A'P'D').V.(A'P'D')'. C'est pourquoi l'écriture XYX' s'applle conjugaison. par exp : ABA' c'est une conjugaison de B
Rappel l'inverse d'une formule
X = ABH'GD'P²G'H
X' = H'GP²'DG'HB'A' (lire à envers et prime<->non-prime)

Parfois on trouve dans la litérature les notations Y^X = XYX' ou Y/X = XYX' , pour la simple raison que ces notations traduisent une propriété de l'opération , en effet .
* (Y^X)^Z = Z(Y^X)Z' = Z(XYX')Z'
= (ZX)Y(X'Z') = (ZX)Y(ZX)' = Y^ZX autrement dit on a la relation
(Y^X)^Z = Y^ZX ce qui correspond bien une propriété des puissances.
de même pour la notation Y/X
* (Y/X)/Z = (XYX')/Z = Z(XYX')Z' = (ZX)Y(X'Z') = (ZX)Y(ZX)' = Y/ZX ce qui correspond bien une propriété de la division.

Les K-formules

Une K-formule c'est une formule qui modifie une seule pièce de la face K laissant ainsi intactes les autres pièces de la face K, elle peut bien sûr modifier les autres faces.
Par ex:

F = D'BDABA' est une H-formule car elle modifie une seule pièce (HDA) de la face Haut.
ζ = [DH] est une B-formule car elle modifie une seule pièce (BAD) de la face Bas, mais c'est aussi une G-formule car elle modifie une seule pièce (HGP) de la face Gauche.

Formules propres

Une formule propre est une formule qui rélalise un travail visé et laisse le reste du Cube invariant, la formule V est propre. Les formules propres sont très recherchées car elles permettent d'appliquer le Principe De Conjugaison sans aucune précaution à prendre.

Mais comment trouve-t-on les formules propres ? comment fabrique-t-on les formules propres ??. Eh ! bien, on les fabrique à partir des K-formule !!

Supposons que S est une G-formule, S modifie la sommet-Gauche (HAG) de la face G et laisse autres pièces de la face Gauche invariantes (elle peut modifier les autres faces bien sûr) alors on peut construire une formule propre. On prend : [SG] = SGS'G'.
Voyons sur un ex

Voici une G-formule ζ = [DH] qui modifie le sommet (HGP) et laisse la face G invariante, on va construire une formule propre à partir de ζ
Il suffit de prendre L = [ζG] = ζGζ'G'

Explication
1. On applique ζ : le sommet (HGP) est échangé, mais le reste du Cube est perturbé
2. On amène le sommet (BPG) -sommet cobay- en (HGP): G
3. On applique ζ' : qui échange le sommet (BPG) et répare le reste du Cube en même temps .
4. On remet le sommet (BPG) dans son emplacement initial: G'
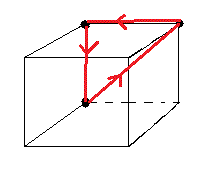
La formule L = ζGζ'G' déplace 3 sommets (HGP)->(BPG)->(HPD) et laisse le reste du Cube invariant.

ζ = [DH]	L = [ζG] = ζGζ'G'

Dans le même ordre idée

Soit ζ² = [DH]² qui pivote le sommet (HGP) et laisse la face G invariante, on va construire une formule propre à partir de ζ²
Comme dans l'exemple précédant on prend L = [ζ²G] = ζ²Gζ²'G'

Explication
1. On applique ζ² : le sommet (HGP) est pivoté, mais le reste du Cube est perturbé
2. On amène le sommet (BPG) -sommet cobay- en (HGP): G
3. On applique ζ²' : qui pivote (BPG) à l'inverse et répare le reste du Cube en même temps.
4. On remet le sommet (BPG) dans son emplacement initial: G'
La formule L = ζ²Gζ²'G' pivote 2 sommets (HGP),(BPG) et laisse le reste du Cube invariant.

ζ² = [DH]²	L = [ζ²G] = ζ²Gζ²'G'

La façon de construire une formule propre comme ci-dessus s'appelle Pricipe De Commutation. Le Pricipe De Commutation s'écrit toujours dans le format: XYX'Y' en abrégeant [XY], c'est pourquoi l'écriture XYX'Y' s'appelle commutation

En Rubik's Cube on utilise 2 principes:
La Conjugaison: X^Y = YXY' et
La Commutation: [XY] = XYX'Y'
YXY' s'appelle un conjugué de X

1 2 3 4 [5] 6

Accueil

DMJ: 25/06/2021