Le groupe du SuperFloppy

A- Les formules (M,.)

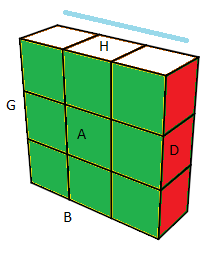
On va nommer les faces et fixer le Cube:
H(aut)=b(lanc), B(as)=j(aune), A(vant)=v(ert), P(ostérieur)=k(lein), G(auche)=o(range), D(roite)=r(ouge)

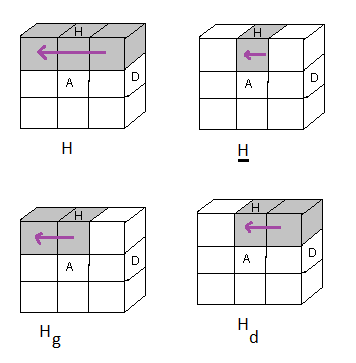
Les rotations
H = tourner 90° dans le sens horaire

Rotations à 90° sens horaire

- Les rotations étendues : H, H , H_g , H_d

- Les rotations de base ou les rotations standards :
{H², B², G², D²}
On pose :
M = < H², B², G², D² >
M = l'ensemble des formules du SuperFloppy
la loi '.' = concaténation

SuperFloppy Cube	D² = / (lire slash)

B- Les configurations (G⁺, .)

Avant d'aller plus loin, précisez bien la notion "permutation", et la notion "orientation"
- Une permutation, c'est qu'il y a un déplacement en cycles des pièces
- Une orientation, c'est qu'il y a plusieurs façons que la pièce se place (se loge) dans son propre emplacement.

Prenons notre SuperFloppy Cube et analysons le:

1. On a 4 sommets qui baladent partout et ils n'ont pas d'orientations donc on a affaire à S₄
2. Les arêtes ne bougent pas ! mais une arête a 2 orientations , donc pour les arêtes on a affaire à Z₂⁴

Finalement l'ensemble des configurations est:
G⁺ = S₄ x Z₂⁴
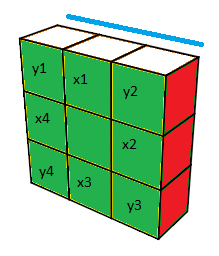
s = (v,x) , v∈S₄ , x∈Z₂⁴
v = (y₁,y₃,y₂,y₄ ) = (1,3,2,4) par ex
x = (x₁,x₂,x₃,x₄ )
x_i = 0 (resp. 1) si la couleur dominante est sur le marquage 0 (resp. 1)
y_i = 0 (resp. 1) si la couleur dominante est sur le marquage 0 (resp. 1)

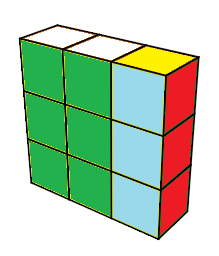
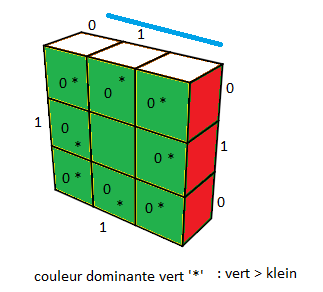
On marque ainsi les facettes :
Pour les sommets : Face Avant = 0, face postérieur = 0
Pour les les arêtess : Face Avant = 0, face postérieur = 1
Couleur dominante (*) : vert (vert > klein)

Nom des pièces	Les facettes marquées

La loi interne de G⁺

On définit la loi '.' de composition sur G⁺ ainsi :
(v,x)(v',x') = (vv', x+x')

C- Action '•' de M sur G⁺

On définit une action '•' de M dans G⁺ ainsi
G⁺ x M --> G⁺
(s,V) --> s•V = t
Vérifiant les axiomes suivants:
A₁ : s•I = s ; élément neutre
A₂ : (s•V)•T = s•(VT) ; associativité
A₃ : a donné,fixé
a•V = a ==> V=I ; librement
A₄ : s•(VT) = (s•V)(s•T) ; compatibilité

D- Le groupe du SuperFloppy (G,.)

Par définition le groupe du SuperFloppy (G,.) est :
G = {s∈G⁺ | s=e•V , V∈M}
Ce sont des configurations provenant de M, les rotations de base

E- Théorème fondamental

On démontre le théorème suivant:
La loi de parité:
(P) : sig(v) = (-1)^k ; k=le nombre de flips des arêtes
G = {s∈G⁺ | s vérifie (P)}

F- Problème de parité

Le problème de parité chez le SuperFloppy est exactement le même problème de parité chez le Square-1
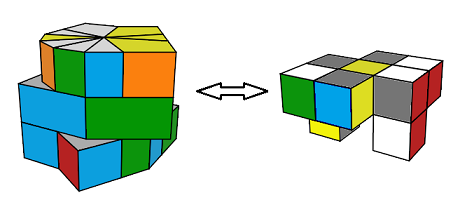
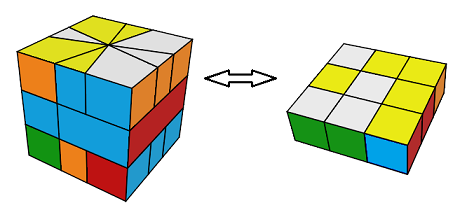
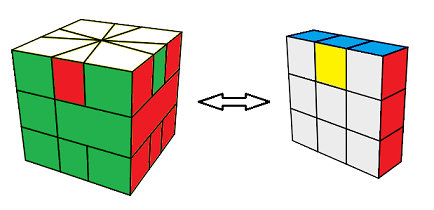
Lorqu ' on mélange le Cube avec des rotations étendues, le Cube change de forme et quand on revient à la forme carré , il se peut que les sommets et les arêtes ne sont plus "en phase"
dans ce cas quand on arrive à la fin de la résolution on peut tomber sur le problème de parité !

Mélangé avec des rotations étendues : Le Cube change de forme

	Forme Carré

état de parité

Pour fixer la parité , il faut utiliser les rotations étendues

G- L' entropie du SuperFloppy

Soit e•V = µ avec V^d = I (<==> µ^d = e)
Par définition l'entropie de µ (ou de V) est :
S = log Ω
où Ω = le nombre d'états ayant le même d

L'entropie	Formule , ordre

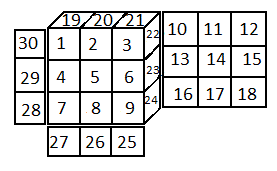
numérotation des autocollants (stickers)

# gap_floppy.txt
#
# 19 20 21
#30 | 1 2 3 | 22 | 10 11 12
#29 | 4 5 6 | 23 | 13 14 15
#28 | 7 8 9 | 24 | 16 17 18
# 27 26 25
#
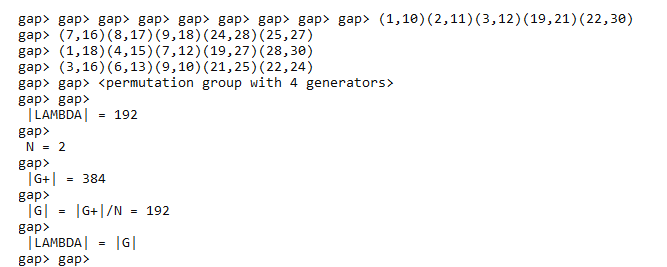
pH2 := (3,12)(2,11)(1,10)(22,30)(19,21);
pB2 := (7,16)(8,17)(9,18)(28,24)(27,25);
pG2 := (1,18)(4,15)(7,12)(19,27)(28,30);
pD2 := (9,10)(6,13)(3,16)(25,21)(24,22);

LAMBDA := Group( pH2, pB2, pG2, pD2 );
N := 2 ;;
Print( "\n |LAMBDA| = ", Size( LAMBDA ) , "\n" );
Print( "\n N = ", N , "\n" );
Print( "\n |G+| = ", Factorial(4) * (2^4) , "\n" );
Print( "\n |G| = |G+|/N = ",( Factorial(4) * (2^4) ) / N , "\n" );
Print( "\n |LAMBDA| = |G|", "\n" );

Nombre d'états

Commentaire

On pourait comparer le groupe de SuperFloppy au groupe du Pyraminx, ou du Pocket.

SuperFloppy:

1. G⁺ = S₄ x Z₂⁴
2. Loi de composition: (v,x)(v',x') = (vv', x+x')
3. Loi de permutations: sig(v) = (-1)^k ;k=nbr flips d'arêtes

Pyraminx:

1. G⁺ = S₆ x Z₂⁶ x Z₃⁴ x Z₃⁴
2. Loi de composition: (u,x,y,z)(u',x',y',z') = (uu', x+u(x'), y+y',z+z')
3. Loi de flips: ∑ x_i = 0 (mod 2)
4. Loi de permutations: sig(u) = 1

Pocket:

1. G⁺ = S₈ x Z₃⁸
2. Loi de composition: (v,y)(v',y') = (vv', y+v(y') )
3. Loi de twists ∑ y_i = 0 (mod 3)

[1]

Accueil

DMJ: 09/11/2024