Le groupe du Void Cube

Rappel les notations

Avant tout rappelons les notations:
(H)aut=(b)lanc, (B)as=(j)aune, (A)vant=(v)ert, (P)ostérieur=(k)lein, (G)auche=(o)range, (D)roite=(r)ouge
(h)aut-intérieur , (a)vant-intérieur , (d)roite-intérieur.

(HA) = l'emplacement Haut-Avant , c'est un emplacement d'une arête
Par abuse de langage on dit aussi l'arête (HA) pour dire l'arête contenue dans l'emplacement (HA)
(bv) = c'est l'arête blanc-vert

(HDA) = l'emplacement Haut-Droite-Avant , c'est un emplacement d'un sommet
Par abuse de langage on dit aussi le sommet (HDA) pour dire le sommet contenu de l'emplacement (HDA)
(brv) = c'est le sommet blanc-rouge-vert

(HA) peut contenir les pièces (jr) ou (bk) , ... càd jaune-rouge ou blanc-klein , ....
(brv) c'est le sommet blanc-rouge-vert
(HDA) peut contenir les pièces (jvr) ou (bkr), ... càd jaune-vert-rouge , blanc-klein-orange , ....

Référentiel

Avant d'aller plus loin, il y a une notion très importante qu'on doit maitriser: le référentiel
Pour comprendre faissons une expérience.
Bob nous donne un Rubik's Cube mélangé à partir d'un état s , il l'a mélangé avec la formule F = HPBAD²B'G, Bob nous demande de retouver l'état s.
Le seul moyen de retrouver l'état s c'est d'appliquer la formule inverse F' = G'BD²A'B'P'H' mais le big problème c'est : Où est le Haut ? le Bas ? l'Avant ?? etc ...!!
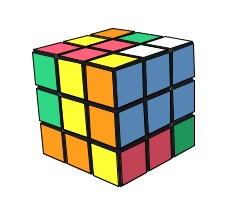Sans ces informations on ne peut rien faire, on peut résoudre le cube mais ça nous sert à rien car on tombe sur l'état résolu, qui n'est pas l'état s demandé.

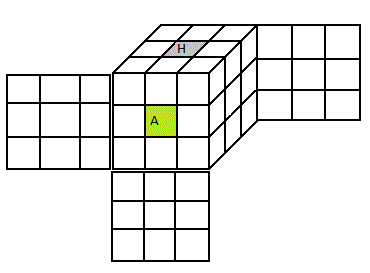Référentiel R

Quand on fixe le centre Haut=blanc, le centre Avant=vert par exp, on dit qu'on a orienté le cube (ne pas confondre avec l'orientation des sommets ou des arêtes) ou on a fixé le cube, ou encore on se place dans le référentiel R (rappel H=blanc, A=vert) . On travaille toujours dans un référentiel, c'est normal puisqu'on parle de H,B,G,D .... il faut savoir où est le Haut , le Bas etc .... Pour avoir un référentiel il suffit de fixer les centres (H) et (A), car en Rubik's Cube les centres ne bougent pas.

Résumons En Rubik's Cube il faut toujours fixé le cube, autrement dit il faut orienter le cube, pour ça on fixe les deux centres (H) et (A) , pour nous c'est (H)=blanc, (A)=vert c'est le référentiel dans lequel nous travaillons et que nous désignons par R

Analyse du Void Cube

Comme le Void Cube n'a pas de centre , pour fixer le cube (orienter le cube) il faut utiliser une arête pour nous c'est: (BA) avec B=jaune, A=vert autrement dit (BA)=(jv) , cette arête jaune-vert doit être invariante, (ne pas bouger, ne pas changer l'orientation) c'est le référentiel du Void Cube et nous le désignons R' (B=jaune, A=vert) ,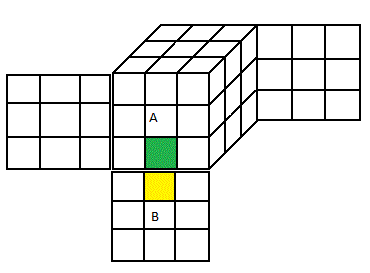

Référentiel R'

Ainsi on supprime les rotations B, A et les remplace par b, a ou encore h, a (c'est pareil) , l'ensemble des formules du Void Cube est donc M = <H,h,a,P,G,D>

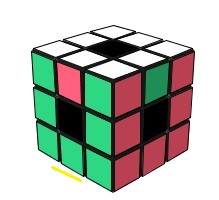
Si on prend M = <H,B,A,P,G,D> càd on mélange le Void Cube avec les rotations {H,B,A,P,G,D} comme en Rubik's Cube , on gènère plus d'états qu'il en faut comme indique la fig ci-dessous

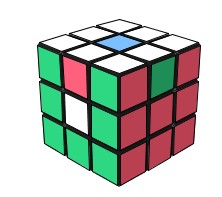Le même état ci-dessous	Le même état ci-dessous

Un état du Void Cube

M = <H,h,a,P,G,D> laisse l'arête (BA) invariante (invariant : ne bouge pas, ne change pas d'orientation, fixe : ne bouge pas, mais peut changer l'orientation) !! ça veut dire qu'on a 11 arêtes seulement au lieu de 12 donc on a affaire à S₁₁ pour les arêtes. Le groupe V⁺ étendu du Void Cube est donc
V⁺ = S₁₁ x Z₂¹¹ x S₈ x Z₃⁸
le groupe du Void Cube V est un sous groupe de V⁺ vérifiant
(u,x,v,y)∈V⁺
∑x_i = 0 (mod 2)
∑y_i = 0 (mod 3)

V c'est aussi les permutations générées par M
On a tout de suite le cardinal de V
|V| = 11! x 2¹¹ x 8! x 3⁸/2x3 = 11! x 2¹⁰ x 8! x 3⁷

Rappelons que la loi dans V est
Pour les arêtes : (u,x)(w,z) = (uw,x+u(z)) pour les sommets c'est pareil.

Le groupe des Spots du Rubik's Cube

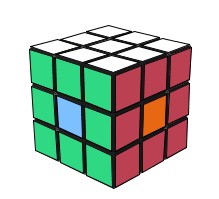
On a vu que plusieurs états du Rubik's Cube correspondent à un état du Void Cube, On va poser la question suivante:
Quels sont les états du Rubik's Cube qui correspondent à l'état résolu du Void Cube ??

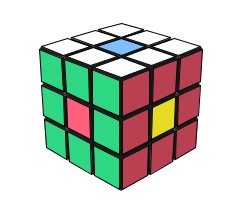Un état du Rubik	Un état du Rubik

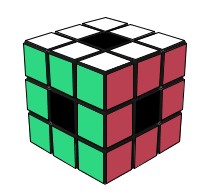
l'état résolu de Void Cube

On va noter H l'ensemble des états du Rubik's Cube qui correspondent à l'état résolu du Void Cube , voyons combien H possède d'éléments, un élément de H c'est un état où les faces ont la même couleur, sauf peut-être le centre. Pour connaitre le nombre d'éléments de H, deux formules vont nous aider

K = (HD²H'aH . D²H²aHa')²
Q = [h,a]

On a:
- Etat résolu du Rubik ⇒ état résolu du Void Cube
- Appliquer K ça donne : 2 centres opposés fixes + 2 centres opposés permutés + 2 centres opposés permutés ⇒ donc on a 3 états de ce type
- Appliquer Q ça donne : 3 centres tournés autour d'un sommet-haut + 3 centres tournés autour du sommet-opposé ⇒ donc pour un sommet-haut on a deux états (sens horaire et sens contraire) comme on a 4 sommet-haut ça fait 8 états de ce type
finalement: 1 + 3 + 8 = 12 états, |H|=12
il n'y en a pas d'autres, en effet ce sont des permutations paires des centres (elles conservervent l'état résolu du Void Cube), et comme il y a 24 permutations des centres S_c=S₄ on a 12 permutations paires

REMARQUE
1. H = < k,q > où k (resp. q) est la permutation associée à K (resp. Q).
k=(1,2)(5,6);
q=(3,5,2)(1,4,6);
2. On pourrait penser que H = S₆ puisqu'on a 6 centres, mais c'est une erreur, car les centres ne bougent pas comme ils veuillent, par exp on ne peut pas avoir blanc<->vert ! les centres sont physiquement soudés entre eux donc on n'a pas toutes les 6! permutations

Groupe des Spots

On va montrer que H est un groupe que l'on nomme le groupe des Spots
- e∈H (e=état résolu, il est dans H)
- Un élement h de H laisse invariant la couleur des faces donc le produit de deux éléments de H est encore dans H, par exp pour la face rouge
h(rouge) = rouge
g(rouge) = rouge
h[g(rouge)] = h(rouge) = rouge ⇒ hg∈H
de même h∈H ⇒ h^-1∈H en effet
h(rouge) = rouge
rouge = h^-1(rouge)
H est donc un groupe, mais malheureusement il n'est pas normal dans G !!!
un groupe normal si on a ghg^-1∈H pour tout g∈G et h∈H il suffit de prendre
g état engendré par (H²D²)³H(H²D²)³H' (tenir le cube: (H)=blanc, (A)=vert)
et h état engendré par (HD²H'aH . D²H²aHa')² (tenir le cube: (H)=blanc, (A)=vert)
on a g=g^-1 (tenir le cube: (H)=blanc, (A)=vert)
ghg^-1 n'est pas dans H puisque les faces n'ont pas la même couleur.

On ne peut pas "diviser" G par H donc pas de groupe quotient G/H , la seule chose qu'on peut avoir c'est des classes G\H = {aH, bH, cH , ... }

NOTE : On démontre que H = A₄ , on peut se demander comment est il possible un truc à 6 centres correspond à un truc à 4 objets, en fait A₄ est le groupe des déplacements (le groupe des symétries) du tétraèdre (le Pyraminx) et ses 6 arêtes correspondent aux 6 centres du cube.

Le Void Cube et les classes du Rubik's Cube

Considèrons l'application suivante: l'ensemble des classes G\H de G vers V
f: G\H -> V
aH -> f(aH) = a ; on prend un état t de G et on oublie les centres a=t sans-centres
1. f est visiblement surjective, en effet un état a de Void Cube on associe la classe aH
2. f est injective: f(aH)=f(bH) ⇒ a=b ⇒ aH=bH
donc f est bijective

On a: G = U aH = aH U bH U cH ... ; les classes forme une partition de G
|G| = ∑_k |aH| où k=nombre de classes
|G| = ∑_k |H| car |aH| = |H|
|G| = k|H|
d'où
k = |G\H| = |G|/|H|
|V| = |G|/12 = 11! x 2¹⁰ x 8! x 3⁷
car G\H et V sont en bijection, on trouve bien le même résultat plus haut.

RESUME

1. M = <H,h,a,P,G,D>
2. V⁺ = S₁₁ x Z₂¹¹ x S₈ x Z₃⁸
   Le groupe du Void Cube V est un sous groupe de V⁺ vérifiant
   (u,x,v,y)∈V⁺
   ∑x_i = 0 (mod 2)
   ∑y_i = 0 (mod 3)
3. V est aussi les états engendrés par les formules de M
4. |V| = |G|/12

[1] 2

Accueil

DMJ: 05/06/2023