Le Square-1

Difficulté: 17/20 difficile

1- Notation

Pour fixer les idées voici la face Avant et le Haut choisies une fois pour tout :

La face Avant c'est la face avec l'équateur comportant le petit rectangle à gauche.
La couleur Haut, c'est la couleur-haut du sommet "correspondant" à l'équateur, c'est-à-dire dont les faces latérales ont les même couleurs avec l'équateur voir fig


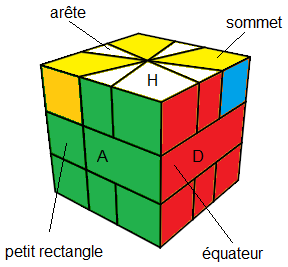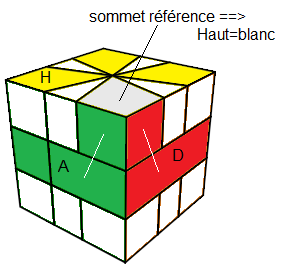Pour nous les couleurs sont donc:
H(aut)=b(lanc), B(as)=j(aune), A(vant)=v(ert), P(ostérieur)=k(lein), G(auche)=o(range), D(roite)=r(ouge)


Les rotations
Pour la famille de Square-1 on adopte la notation additive '+'
1 sommet = 2 arêtes

exemple: (3-2B)/
3 = tourner 3 arêtes (1 sommet = 2 arêtes) de la face Haut dans le sens des aiguilles d'une montre.
-2B = tourner 2 arêtes de la face Bas dans le sens contraire.
/ = tourner la face Droite 180° (/ = slash)

Les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!

2- Observation

Comme nous avons déjà dit plus haut, le Square-1 est formé par 16 petits pièces divisé en 2 catégories:
1. Les arêtes (8): portant 2 couleurs, elles se déplacent librement.
2. Les sommets (8): portant 3 couleurs, ils se déplacent aussi librement.

Mais les arêtes ne se mettent jamais à une place des sommets, et inversement. Chaqu'un reste dans son groupe, les arêtes dans le groupe des arêtes, les sommets dans le groupe des sommets.

[1] 2

Accueil

DMJ: 12/02/2024