Résolution du Square-1

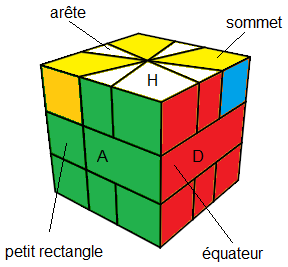
1- Notation

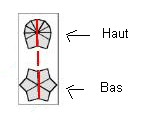
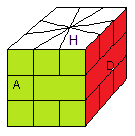
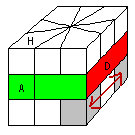
Pour fixer les idées voici la face Avant et le Haut choisies une fois pour tout :

La face Avant c'est la face avec l'équateur comportant le petit rectangle à gauche.
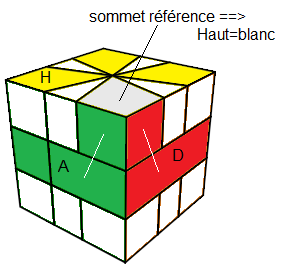
Trouver le Haut : La couleur Haut, c'est la couleur-haut du sommet "référence", c'est-à-dire dont les faces latérales ont les même couleurs avec l'équateur voir fig
Si on ne trouve pas le Haut c'est que le Haut est en Bas, faites donc /6+6B/


Pour nous les couleurs sont donc:
H(aut)=b(lanc), B(as)=j(aune), A(vant)=v(ert), P(ostérieur)=k(lein), G(auche)=o(range), D(roite)=r(ouge)


Les rotations
Pour la famille de Square-1 on adopte la notation additive '+'
1 sommet = 2 arêtes

exemple: (3-2B)/
3 = tourner 3 arêtes (1 sommet = 2 arêtes) de la face Haut dans le sens des aiguilles d'une montre.
-2B = tourner 2 arêtes de la face Bas dans le sens contraire.
/ = tourner la face Droite 180° (/ = slash)

Les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!

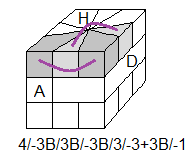
Phase I: Retrouver la forme cubique

Lorsqu'on mélange le Square-1, il donne des formes très bizarres,.... il faut d'abord le mettre sous la forme cubique, avant la résolution.
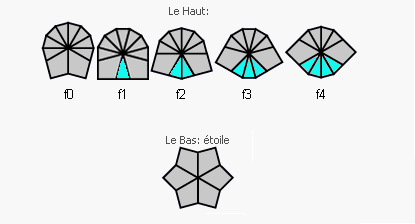
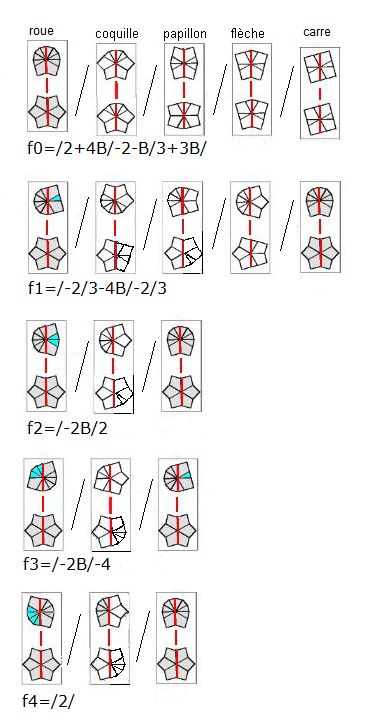
Pour cela on met le Bas sous la forme d'une "étoile" . On pousse donc toutes ces 8 arêtes vers le Haut. Une fois le Bas a la forme d' étoile, le Haut ne peut prendre que 5 formes distingues ci-dessous.


En poussant les arêtes vers le Haut on essaie de les regrouper ensemble pour avoir la forme f0 comme indique fig ci-dessous


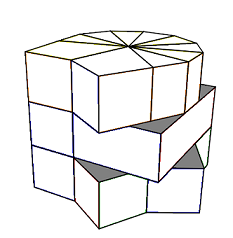
à partir de cette forme (f0) on reconstitue le cube, la restruction se fait comme indique la fig

Bien alligné puis on coupe par / (slash)

Parfois on a besoin de corriger l'équateur : /6/6/6

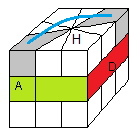
Phase II: Restituer les faces

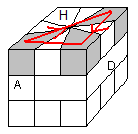
Il faut d'abord chercher la couleur Haut. En tournant le Haut, cherchez un sommet "référence". La couleur Haut c'est la couleur-haut de ce sommet.
S' il n'y a aucun sommet référence, c'est que la face Haut est en Bas, il faut donc la remonter avec: /6+6B/


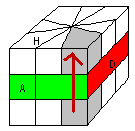
1) Ranger les sommets Bas
Si un sommet Bas est dans une mauvaise position, on descend n'importe quoi ça l'oblige à remonter !!!

(HDA)->(BAD) = -B/3/3/6/B (en phase)

2) Permuter deux sommets Haut
Echanger 2 sommets Haut-Gauche:

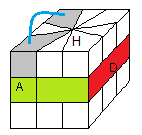(HGP)<->(HAG) = 3/-3+3B/3/-3B/3B/-3B/ (en phase)

3) Ranger les arêtes Bas
On range les arêtes Bas par la formule:
(HD)->(BD) = 1/-3B/-1-4B/1+B/3B/3B/-1
Si une arête Bas n'est pas à sa place, on descend n'importe quoi ça l'oblige à remonter !!!

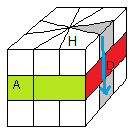(HD)->(BD) = 1/-3B/-1-4B/1+B/3B/3B/-1 (en phase)

4) Ranger les arêtes Haut
On range les arêtes Haut par la formule
(HG)->(HD)->(HP) = 1/-3B/-1/3/1/3B/-1/-3/

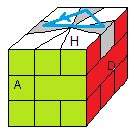(HG)->(HD)->(HP) = 1/-3B/-1/3/1/3B/-1/-3/ (en phase)

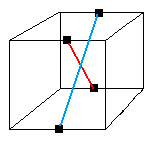
III Probème de parité

On a un problème de parité c'est quand on a violé la loi de parité : forme cubique et sig(sommets)=sig(arêtes) , autrement dit c'est quand on a 2 arêtes ou 2 sommets à échanger, voir la fig.
faites:
(HA)<->(HD) = (/-3/) + (3B/-3B/3B/) + (2/2B/-2/) + (4/-2B/2B/) + (-1+4B/6-3B/6/3)
Remarque : On a 50% d'avoir la parité !

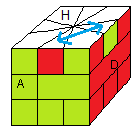(HA)<->(HD)= /-3/ 3B/-3B/3B/ 2/2B/-2/ 4/-2B/2B/ -1+4B/6-3B/6/6+3B	ET hup là !! si vous n'êtes trompé

Commentaire sur le problème de parité

La Square-1 possède une loi de parité.
On pose :
S = 1/3/-1
Q = 1/3B/-1
E = -B/3/B
T = -B/3B/B
Les rotations standards sont {3, 3B, S, Q, E, T}
à partir de ces rotations on démontre qu'on a une loi de parité.
Loi de parité:
-Forme cubique et sig(sommets) = sig(arêtes)

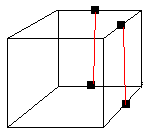
Formules supplementaires

Pour les sommets (perturber les arêtes)

4/-3B/3B/-3B/3/-3+3B/-1	/ 3+3B/3/ 3+3B/3/ 3+3B/3/

(BAD)->(HDA) = 1/-3B/-3B/6B/-1	(BAD)<->(BDP) = 1/-3B/3/-3/-3+3B/-3/2

(HAG)->(HPD)->(HDA) = 1/3B/2/-3/-2/-3B/2/3/-3 (sans toucher les arêtes)

Pour les arêtes (sans perturber les sommets)

1/-1-B/B	2B/3B/1+B/-1-4B/-2B

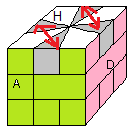(HG,HA)(HP,HD) = /3+3B/3B/1+B/-1-4B/-3-3B/	(HP)->(HG)->(HD) = 1/-3B/-1/3/1/3B/-1/-3/

J'ai découvert une transformation assez intéressante car une fois avoir une formule pour le Haut, on a une autre formule pour le Bas, son semblable, son symétrique, son homologue,.
Son semblable :

1. '-' ⇔ '+'
2. Haut ⇔ Bas

Exemple:
Voici une formule valable pour le Haut
E = 1/-3B/-1/3/1/3B/-1/-3/
Et ^sE son homologue pour le Bas
^sE = -B/3/B/-3B/-B/-3/B/3B/

On peut aussi utiliser l' astuce suivante (ce qui donne le même effet que l'homologue)
Astuce :

1. Retourner le cube Haut<->Bas
2. Avec le grand-rectangle à gauche
3. -1
4. Appliquer la formule.

1 [2]

Accueil

DMJ: 12/02/2024