QuadStripe
 Inventeurs: Andreas Nortmann
Inventeurs: Andreas Nortmann
Année: 2004, 2018 (Z-CUBE)
Nombre d'états: 580 x 432 = 250560
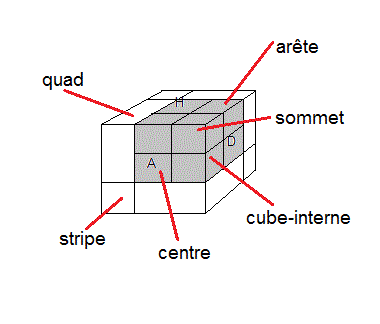
Ce bandage est intéressant (on l'appelle par fois "3 quads 3 stripes") , il a un petit cube-intérieur en (HDA), des carrés (quads) et des barres (stripes) qui entournent ce petit cube.
NOTE : Pour calculer le nombre d'états, on peut commencer par calculer le nombre de formes ça vaut 580 (donné par un programe informatique) et à chaque forme on a 432 états (on garde la même forme mais on permute ou pivote des pièces avec leurs couleurs),
donc le nombre d'états est 580 x 432
Le QuadStripe
| Difficulté: 14/20 moyen+ | ||||||
|
|
||||||
31
Mai
2014
Commentaire
La résolution est intéressante parce que les formules sont assez longues , parfois 30 rotations !!!
1- Notation
 |
 |
 |
 |
| recto | verso |
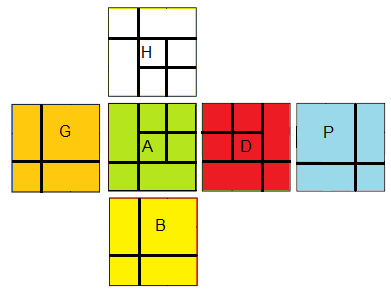
On va nommer les faces et les couleurs:
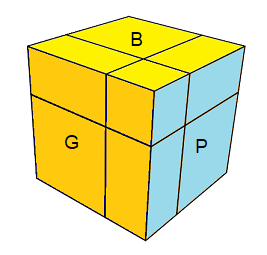
(H)aut=(b)lanc , (B)as=(j)aune , (A)vant=(v)ert , (P)ostérieur=(k)lein , (G)auche=(o)range , (D)roite=(r)ouge.
Les rotations
A = tourner 90° la face Avant dans le sens des aiguilles d'une montre.
A' = tourner 90° dans le sens contraire
A² = tourner 180°
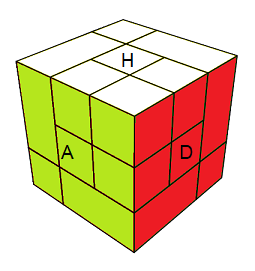
Dans les dessins, la face Avant porte la couleur verte, et on voit le Haut (blanc) et la Droite (rouge).
On écrit (HA) pour désigner le arête Haut-Avant ou (HDA) le sommet Haut-Droite-Avant
Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!
2- Observation
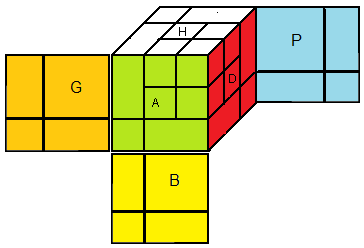
Le QuadStripe est formé par 14 pièces:1. 3 centres
2. 3 arêtes
3. 2 sommets
4. 3 carrés
5. 3 barres (long sommet)
 |
|
| QuadStripe |
Le QuadStripe est intéresant comme bandage parce que la résolution utilise des formules très longues, et pratiquement il est difficile à se souvenir.
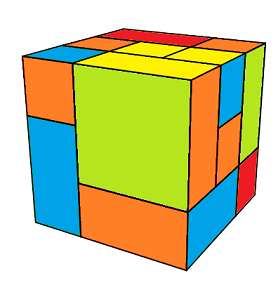 |
|
| QuadStripe mélangé |
3- Formes et états
On prend le cube bridé à l'état résolu sans couleur, c'est-à-dire on enlève les stickers ou les tiles, on a là une "forme". Si on mélange (ce cube bridé sans couleur) on trouvera alors une autre forme. Une forme est donc un état sans couleur. Voici deux formes de ce twist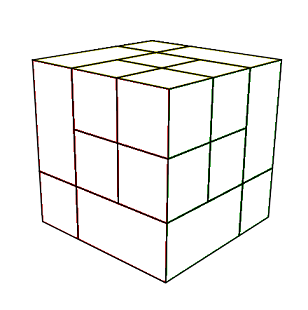 |
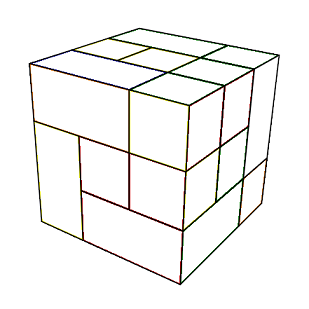 |
| forme 1 | forme 2 |
Mais une forme génère des états (on garde la même forme mais on permute ou pivote les pièces avec leurs couleurs) par ex: la forme 2 donne par exemple deux états ci-dessous :
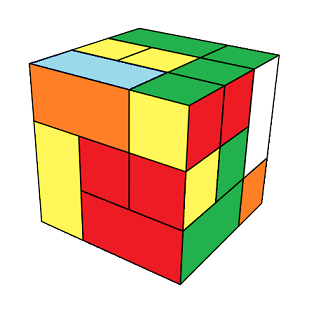 |
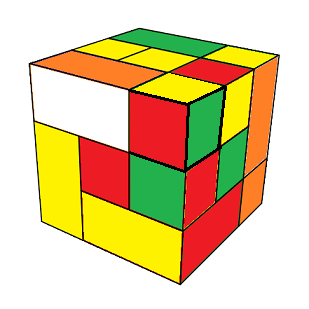 |
| un état | un autre état |


