Skewb Diamond
 Inventeurs: Tony Fisher
Inventeurs: Tony Fisher
Année: 1991
Nombre d'états: 6!.26 x 4!/2.2.2 = 138240
Diamètre: 10
Rotations de base : {B,A,G,D}
-Les sommets ont une permutation paire ==> /2
-Le nombre d'orientations des sommets est pair ==> /2
-Les centres ont une permutation paire ==> /2
Un programme nous donne:
Distance: nombre d'états
0: 1
1: 8
2: 48
3: 288
4: 1632
5: 8568
6: 36114
7: 74799
8: 16547
9: 220
10: 15
===========
Total: 138240
Le Skewb Diamond est simplement un Skewb mais le rôle des pièces se permutent !!!
Skewb Diamond: Sommet => Centre (Skewb)
Skewb Diamond: Centre => Sommet (Skewb)
Le Skewb Diamond (il a 8 faces) est beaucoup plus simple car les Centres (Sommet en Skewb) ne sont pas orientés.
Skewb Diamond
| Difficulté: 8/20 facile+ | ||||||
|
|
||||||
11
Dec
2013
Commentaire
 |
|
| Skewb Diamond désassemblé |
Les centres de Skewb Diamond sont divisés en 2 camps : 4 centres liés (liés au core) et 4 centres libres ,
On ignore les centres liés
On tient le twist ainsi: Les 4 centres liés sont: Haut, Postérieur, Gauche, Droite
G+ = 6!.26 x 4!
Voici un script en GAP qui calcule le nombre d'états du Skewb-Diamond
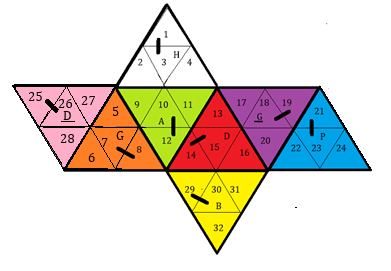 |
|
| numérotation des autocollants |
#gap_skewb-diamond.txt
#rotations disponibles
pH := (4,2,1)(17,9,25)(13,5,21)(11,27,19)(10,26,18);
pB := (29,31,32)(8,16,24)(12,20,28)(14,22,6)(7,15,23);
pA := (11,12,9)(4,14,5)(17,29,27)(13,8,2)(3,15,7);
pP := (21,24,22)(19,28,31)(1,6,16)(25,32,20)(18,26,30);
pG := (5,8,6)(27,12,32)(2,14,24)(9,29,28)(10,30,26);
pD := (13,16,14)(11,20,29)(4,22,8)(17,31,12)(10,18,30);
pGs := (17,19,20)(13,1,22)(11,25,31)(4,21,16)(3,23,15);
pDs := (27,28,25)(2,6,21)(9,32,19)(5,24,1)(3,7,13);
#rotations etendues (violer les lois)
pS := (4,2)(17,9)(13,5)(11,27); #permutation impaire des sommets
pC := (10,26);#permuation impaire des centres
pT := (4,13)(11,17);#monotwist
#les 4 centres liés = H,P,G,D
#rotations de base : B,A,G,D LAMBDAPLUS := Group( pB, pA, pG, pD, pS, pC, pT ); # correspond rotations etendues
LAMBDA := Group( pB, pA, pG, pD ); # correspond rotations de base
N := 2*2*2 ;; #nombre de contraints
Print( "\n" );
Print( "|LAMBDA+| = ", Size( LAMBDAPLUS ) , "\n" );
Print( "|LAMBDA| = ", Size( LAMBDA ) , "\n" );
Print( "N = ",N , "\n" );
Print( "|G+| = ", Factorial(6) * (2^6) * Factorial(4) , "\n" );
Print( "|G| = |G+|/N = ", (Factorial(6) * (2^6)* Factorial(4) ) /N , "\n" );
La résolution se fait comme le Bandage Cube ... On place pièce par pièce ...
1- Notation
Placez le puzzle sur la table avec les 4 centres liés sont: Haut, Postérieur, Gauche, Droite comme indique la fig ci-dessous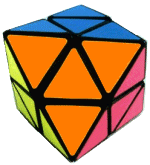 |
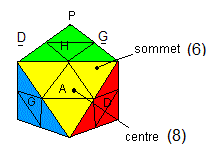 |
Les rotations
H(aut) , B(as) , A(vant) , P(ostérieure) , G(auche) , D(roite).
D=opposé D, G=opposé G
Rotations de base : B,A,G,D
G = tourner 120° dans le sens des aiguilles d'une montre (sens horaire).
G' = tourner -120° (dans le sens anti-horaire)
 |
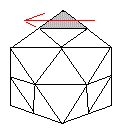 |
| Rotation A | Rotation P |
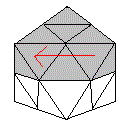 |
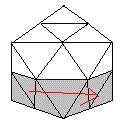 |
| Rotation H | Rotation B |
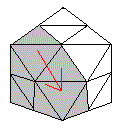 |
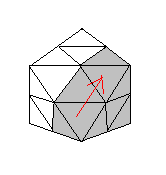 |
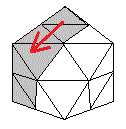
| Rotation G | Rotation D |
 |
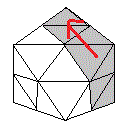 |
| Rotation D | Rotation G |
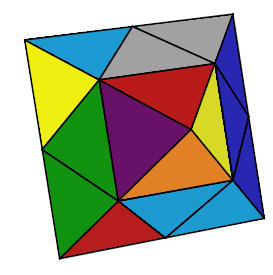
2- Observation
Le Skewb Diamond est formé par :1. Les centres (8) : triangles. (une couleur mais 3 orientations, ils tournent!)
2. Les sommets (6): pyramides. (4 couleurs , mais 2 orientations)
 |
|
| Essayez: [A'G] = A'GAG' |


