L' Octahedron VTO (Vertex Turning Octahedron)
25
Fer
2013
Octahedron VTO
Inventeurs: Christoph's Jewel
Année: 2009
Nombre d'états: 46 x 12!.212 x 46/2x2
Il est vraiment étonnant que l'Octahedron VTO ressemble beaucoup au Pyraminx et la résolution se fait pratiquement pareil, pratiquement même style , même formules ...
Alors que l' Octahedron FTO est complétement différent, sa résolution est bien plus complexe.
1- Notation
Faces :
(A)vant, (H)aut, (
D)roite-opposé, ...
Rotations :
G(auche), D(roite), P(ostérieur) ...
G = tourner 90° dans le sens des aiguilles d'une montre.
G' = tourner -90° (dans le sens contraire)
G² = tourner 180°
On va choisir la face Avant
vert, Haut
blanc une fois pour tout
d = la face opposé à D
Dans les dessins, la face Avant porte la couleur
verte, et on voit le Haut (
blanc) .
On écit (H
D) pour désigner l'arête Haut-Droite-opposé
(H
D)° = pivoter l'arête (H
D)
Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!
2- Observation
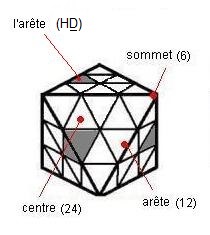
L'Octahedron VTO est formé par 22 petits triangles divisés en 3 catégories:
1. Les centres (24) : portant une seule couleur, ils se regroupent 3 par face , ils bougent un peu !.
2. Les arêtes (12): portant 2 couleurs, elles se déplacent librement et partout, elles ont 2 orientations.
3. Les sommets (6): portant 4 couleurs, ils ne servent à rien !!!! (juste pour cacher les vis ??)
Finalement seules les arêtes jouent un rôle important.
Mais les arêtes ne se mettent jamais à une place des sommets, ou des centres et inversement. Chaqu'un reste dans son groupe,
les arêtes dans le groupe des arêtes, les sommets dans le groupe des sommets, les centres dans le groupe des centres.
 |
|
| Exemple: [GD'] = GD'G'D |
|
[1] 2
Accueil
DMJ: 08/09/2022
