Le groupe du Pocket

L'ensemble des configurations G⁺

Le Pocket est un Rubik's Cube sans arêtes ni centres !! donc l'étude sera comme le Rubik's Cube mais beaucoup plus simble.

Imaginons qu'on a supprmé le core, les sommets peut permuter, pivoter sans contraites,... par ex on peut pivoter un seul sommet à 120° !!!
Un sommet se balade par tout on a donc affaire à S₈ ensuite un sommet a 3 orientations on a donc affaire à Z₃⁸ finalement on est en face d'un truc comme ça:
G⁺ = S₈ x Z₃⁸ , c'est l'ensemble des confugurations.

La loi '.' de (G⁺,.)

On voudrait définir une loi de composition '.' sur G⁺ afin que (G⁺,.) fasse un groupe.
Soient (v,y) et (v',y') deux éléments de G⁺
(v,y)(v',y') = (w,z)
Comment trouver w et z ?
Pour w on voit facilement que w = vv' , car si on déplace les pièces par v puis par v' , on déplace les pièces bien par vv'.
Pour trouver z c'est plus compliqué ... ça se fait en plusieurs étapes . Allons-y mais d'abord on doit préciser les rotations de base et fixer le twist :

Rotations de base : {H,B,A,P,G,D}
Fixer le twist : H(aut)=b(lanc), B(as)=j(aune), A(vant)=v(vert), P(ostérieur)=k(lein), G(auche)=o(range), D(roite)=r(rouge)

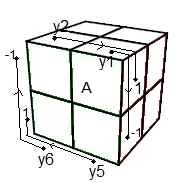
1. Marquage des facettes

Imaginez d'une part, que on a des "emplacements" à 3 facettes marquées comme indique la fig1 ci-dessous

fig1: diagramme de marquages

2. Couleur dominante

Et d'autre part, les sommets (numérotées) ayant 3 couleurs (comme indique la fig2) dont l'une est dominante.
Les couleurs dominantes : blanc > jaune > vert > klein > orange > rouge (les couleurs dont le marquage est zéro 0)

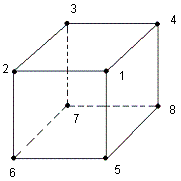sommets numérotés	fig2

Voici les 8 sommets avec leur couleur dominante en première + sens horaire :
y₁=(brv), y₂=(bvo), y₃=(bok), y₄=(bkr),
y₅=(jvr), y₆=(jov), y₇=(jko), y₈=(jrk)

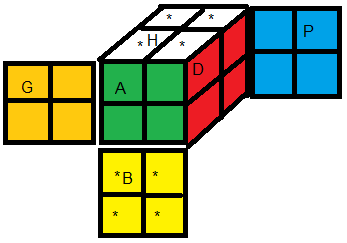Couleur dominante "*"

3. Orientation des sommets

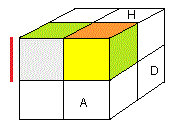
Les sommets y_i se baladent pour se placent dans les emplacements, à chaque fois que la couleur dominante se trouve sur une facette marquée 1 son orientation vaut 1 (1 twist) , sur -1 son orientation vaut -1 (-1 twist) , sur 0 son orientation vaut zéro (0 twist, 0=bien orienté). Par exemple, le sommet y₆=(jov) se place en (HDA) avec jaune = A alors y₆ vaut -1 (-1 twist) car la couleur dominante jaune est sur la facette -1, de même pour le sommet (brv)=y₁ dans (HAG) avec blanc = A alors y₁=1 (1 twist) car la couleur dominante blanc se trouve sur 1 .

blanc, jaune = couleurs dominantes

4. Loi de composition

On note : e•A = s = (q,b)
Pour dire que la rotation A engendre l'état s=(q,b) où q=permutation et b=orientation,
pour trouver q et b, on utilise le diagramme des numérotations et le diagramme des marquages.

diagramme des numérotations	diagramme des marquages

On voit que pour la rotation A, q vaut : q = 1->5->6->2 = (1,5,6,2)
Pour trouver l'orientation b , on utilise le diagramme de marquage


et on voit que b = (-1,1,0,0,1,-1,0,0)
finalement on a:
e•A = (q,b) avec
q = (1,5,6,2)
b = (-1,1,0,0,1,-1,0,0)
Ainsi on peut trouver les états associés pour les autres rotations H,B,P,G,D.

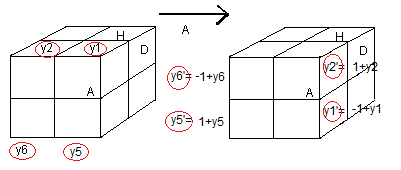
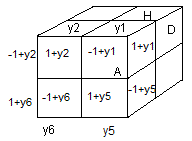
D'après le marquage on a:
(HDA)=(y₁,1+y₁,-1+y₁), (HAG)=(y₂,1+y₂,-1+y₂) ,
(BAD)=(y₅,1+y₅,-1+y₅), (BGA)=(y₆,1+y₆,-1+y₆) .
Les y_i sont placés sur la couleur dominante

Les sommets numérotés

y'₁ = -1+y₅
y'₂ = 1+y₁
y'₃ = y₃
y'₄ = y₄
y'₅ = 1+y₆
y'₆ = -1+y₂
y'₇ = y₇
y'₈ = y₈

Or pour la rotation A on a:
Permutation: q = (1,5,6,2)
Orientation: b = (-1,1,0,0,1,-1,0,0)
on en déduit:
y' = b + q(y)

Soit F≠I une formule avec l'état associé (v',y').
Une formule F≠I commence toujours par une rotation de base, par ex A (état (q,b)) et le reste T (état (v,y)) on peut alors écrire :
F = AT
(v',y') = (q,b)(v,y) = (qv,b+q(y))
ce qui suggère la loi dans (G⁺, .) est :
(v,y)(v',y') = (vv',y+v(y'))

Loi des twists

Loi des twists: la somme des orientations des sommets est un multiple de 3

(T) : ∑ y_i = 0 (mod 3) ou en abrégé y = 0 (mod 3) avec y = (y₁,y₂,y₃,...,y₈)
on dit qu'il y a une conservation des twists .

==> (i) Pour une rotation de base, A par ex et l'état (q,b) associé on a :
b = (-1,1,0,0,1,-1,0,0) on a bien b=0 (mod 3)
On peut vérifier ainsi que le vecteur d'orientation des autres rotations de base est aussi un multiple de 3.

==> (ii) Une formule Q est une suite finie de rotations de base, ceci nous suggère de démontrer la loi des twists par récurrence sur la longueur de Q: |Q|

¤ Pour n=1 , les rotations de base ont tous un vecteur d'orientation un multiplie de 3 d'après (i)
¤ Supposons à l'étape n , la propriété est vrai; Hypothèse de Récurrence (HR)
¤ Voyons si à l'étape n+1, cette propriété reste encore vraie

Or on passse de n à n+1 par:
Q = VZ ; avec |V|=n , Z=rotation de base
(v',y') = (v,y)(q,b)
y' = y +v(b)
comme
y = 0 (mod 3) ;HR
et b = 0 (mod 3) ==> v(b) = 0 (mod 3) ,v ne change rien sur le modulo
donc
y' = 0 (mod 3)

la loi des twists est ainsi démontrée.

Le groupe du Pocket

Le groupe G du Pocket est un sous-groupe de G⁺, ce sont des configurations provenant de M.
Par définition : G = {s=(v,y)∈G⁺ / e•V=s, V∈M} ; e=état résolu

Résumé
G⁺ = S₈ x Z₃⁸ c'est l'ensemble des configurations.
G⁺ muni la loi suivante forme un groupe :
(v,y)(v',y') = ( vv', y + v(y') )
Le théorème fondamental de la Cubologie dit que G vaut:
G = {(v,y)∈G⁺ / y = 0 (mod 3) }
ce sont des configurations vérifiant la loi des twists (T)

On dit aussi que G⁺ est l'étendu ou l'extension de G
D'après la loi (T) le nombre de contraintes N est : N=3

|G| = |G⁺| / N
|G| = |S₈| x |Z₃⁷|
|G| = 8! 3⁸/3 = 88 179 840

[1] 2

Accueil

DMJ: 16/10/2024