Le Professor (Rubik 5x5x5)
| Difficulté: 19/20 difficile+ |
|
|
15
Dec
2017
Professor
Inventeurs: Udo Krell
Année: 1990 (V-Cube5: Puzzle Design Competition 2008)
Nombre d'états: 12!.210 x 8!.37 x (24!)3 / (4!6)2
Formule générale: R2k+1 = 12!.210 x 8!.37 x (24!)(k²-1) / (4!6)(k-1)k
Vous savez peut-être résoudre parfaitement le Revenge, et maintenant vous avez envie de passer au niveau supérieur avec le Professor !!!!
C'est un cube de 6 faces, chaque face portant une couleur, le cube est composé de p=6n²-12n+8=98 pièces. Lorsqu'on tourne une face les pièces bougent
ce qui fait que les faces perdent sa couleur initiale (en sortant de l'usine). Le but c'est de reconstituer le cube à l'état d'origine, chaque face portant une seule couleur.
Les rotations de base: {H,B,A,P,G,D,h,b,a,p,g,d}
1- Notation
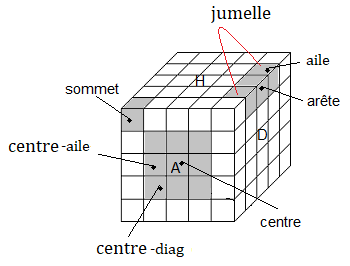
Pour fixer les idées voici la couleur des faces choisies une fois pour tout :
H(aut)=b(lanc), B(as)=j(aune, A(vant)=v(ert), P(ostérieur)=k(lein), G(auche)=o(range), D(roite)=r(ouge)
h(aut-intérieur) , b(as-intérieur), a(vant-intérieur) , p(ostérieure-intérieur) , g(auche-intérieur) , d(roite-intérieur).
Les rotations
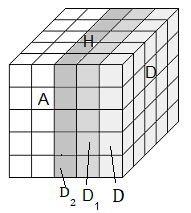
D
ij , i = début, j=fin i≤j ,i=0,1.
Convention: D
0 = D , D
ii = D
i
Exemples: D
1 = d , D
01 = D*
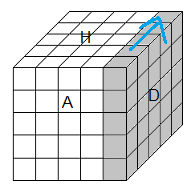
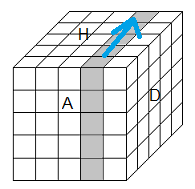
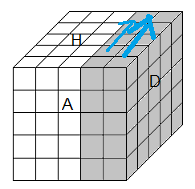
D = tourner 90° la face Droite dans le sens horaire.
D' = tourner -90° (sens anti-horaire)
D² = tourner 180°
d = tourner 90° la tranche droite dans le sens horaire.
D* = tourner 90° le bloc Droite (Dd) dans le sens horaire.
Dans les dessins 3D, la face
Avant porte la couleur
verte, et on voit le
Haut (blanc) et la
Droite (rouge).
Le point '.' et les parenthèses qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!
 |
 |
| Nom des pièces |
D |
 |
 |
| d |
D* |
 |
|
| D0 = D, D1 = d |
|
2- Observation
Comme nous avons déjà dit plus haut, le Professor est formé par p=98 pièces divisés en 4 catégories:
1. Les sommets (8): portant 3 couleurs (3 orientations), ils se déplacent et se pivotent.
2. Les ailes : 1 familles-ailes de (24), portant 2 couleurs (pas orientation !), elles se déplacent.
3. Les arêtes (12) : portant 2 couleurs (2 orientations), elles se déplacent et se pivotent.
4. Les centres : 2 familles-centres de (24), portant une seule couleur, et 6 centres fixes (inertes) au centre de la face, c'est le fixe qui détermine la couleur de la face.
Mais les ailes, les arêtes ne se mettent jamais à la place des sommets, ou des centres et inversement. Chaqu'un reste dans son groupe,
les ailes dans le groupe des ailes,les arêtes dans le groupe des arêtes, les sommets dans le groupe des sommets, les centres dans le groupe des centres.
[1] 2
AccueilDMJ: 28/08/2024
