La rencontre du troisième Copter

Tout a commencé...

Tout a commencé par une balade sur la Toile, de forums en forums, de sites marchants en sites marchants ... et là je tombe sur un twist vraiment joli j'aime la forme cubique et celui là était cubique et a un design vraiment joli, son nom de code est Curvy Copter III


J'ai donc en commandé un. Une fois la commande est passée je commence à chercher les informations de ce twist : nom de l'inventeur, année d'invention ...
Puis le temps de la résolution arrive...

Analyse

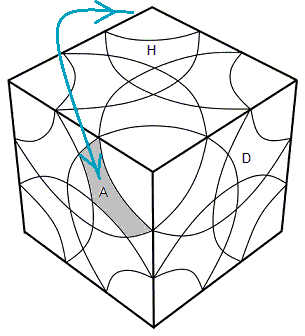
Voyons ce que subit le twist par la simple rotation de base A (180°):
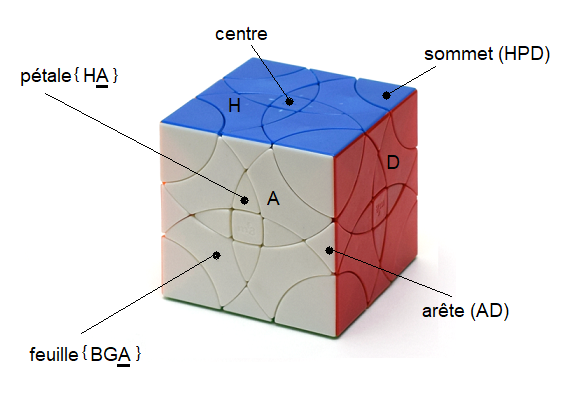
1. d'abord l'arête (HA) pivote mais elle ne se déplace pas.
2. à chaque rotation A, on ajoute 3 (ou zéro 0) à l' orientation des sommets, donc le nombre d'orientations des sommets est un multiple de 3
3. et puis la rotation A engendre une permutation u des pièces
u = sfpc ; s(ommets), f(euilles), p(étales), c(entres).

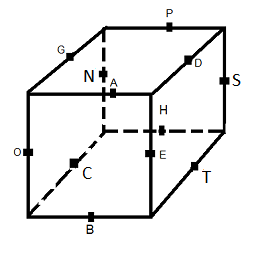
Rotation A

1. s = (s₁,s₂)
2. f = (f₁,f₂)(f₃,f₄)
3. p = (p₁,p₂)(p₃,p₄)(p₅,p₆)
4. c = (c₁,c₂)

a) On voit que les sommets, les pétales, les centres, sont synchronisés (en phase) puisque sig(s)=sig(p)=sig(c)

b) Les feuilles ont une permutation paire , sig(f) = paire = 1

c) Si on désigne k le nombre de pivotements (à 180°) des arêtes, par définition la direction des arêtes vaut: dir(arêtes) = (-1)^k
on dit que la direction des arêtes est paire pour 1, impaire pour -1
On voit donc que les centres sont aussi "en phase" avec les orientations des arêtes sig(centres) = dir(arêtes)

Réflexion

I. Supposons que tous les arêtes soient bien orientées, leur direction vaut : dir(arêtes)=(-1)⁰ = 1 (pair) , comme les centres et les orientations des arêtes sont en phases, donc les centres ont un état pair . Seules les permutations paires suffisent pour ranger les centres or les permutations paires sont engendrées par les 3-cycles, autrement dit il suffit d'un 3-cycle-centres (et les conjugaisons) pour placer tous les centres. Essayons donc Z = [DA] = DAD'A' = DADA = (DA)² qui donne bien un 3-cycle-centres

II. Lorsque les centres sont bien rangés, pour le même raisonnement qu'en I, il suffit simplement un 3-cycle-sommets pour placer (pas ranger) tous les sommets, je trouve
Q = (DADP)²
Une fois placé tous les sommets , il faut maintenant une formule pour les orienter
Voyons ce que fait Q:
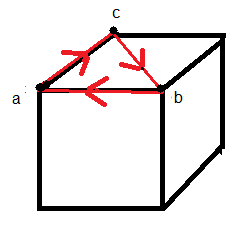
Q déplace 3 sommets en les pivotant, l 'idée est donc de tourner le cube puis remettre en place les sommets, on aura alors forcement pivoté les sommets !

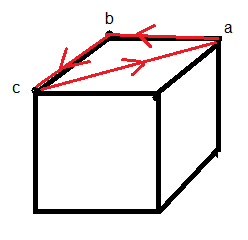
Q	tH' = tourner le cube entier suivant H'

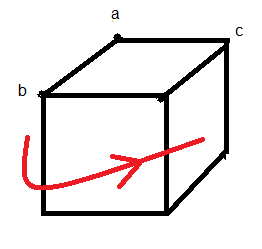
Remettre les sommets en place

On trouve K = (DADP)²(ADAG)² qui pivote les 2 sommets.

III. Pour les feuilles si on observe bien, la permutation f = (f₁,f₂)(f₃,f₄) échange 2 feuilles (f₁,f₂) d'une orbite et 2 autres feuilles (f₃,f₄) d'une autre orbite, donc pour chaqu'orbite les feuilles sont en phase avec les centres, ça signifie que pour ranger les feuilles on a besoin simplement un 3-cycle. je trouve
X = (AEDE)²

IV. Pour les pétales c'est pareil, on a besoin aussi un 3-cycle pour ranger les pétales
Je trouve Y = (DG)²PAP .(GD)²PAP

Finalement on peut restaurer le cube avec 5 formules à condition de le mélanger avec les 12 rotations de base {A, G, P, D, ....} à 180°

1. Z = (DA)² ; centre
2. Q = (DADP)² , K = (DADP)²(ADAG)² ; sommet
3. X = (AEDE)² ; feuille
4. Y = (DG)²PAP .(GD)²PAP ; pétale

Changement d'orbite

Pour le changement d'orbite, il suffit de reprendre les 4 formules du Curvy Copter.
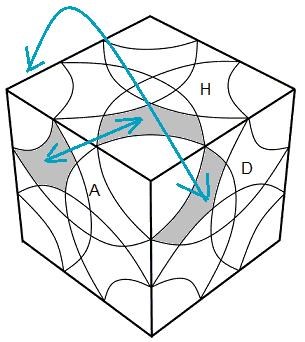
**Mouvement qui échange 2 feuilles des orbites différents.

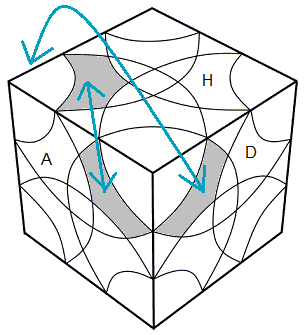(HDA, HAG) (HDA, HAG) = doAo'd'A	(HDA, HAG) (HDA, HAG) = e'g'AgeA

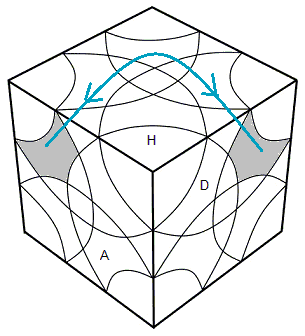
**Mouvement qui échange 2 feuilles du même orbite.

(HAG, HPD) = DG. (doAo'd'A) .GD	(HDA, HGP) = DG. (egAgeA) .GD

Ces formules déplacent d'autres pièces que les feuilles, mais ce n'est pas important on s'occupera ces pièces plus tard.

Structure mathématique

Il y avait un problème qui me hante depuis toujours: La parité du Square-1 . En effet la parité du Square-1 est très mystérieuse on ne comprend pas vraiment ce qui se passe ...
Grâce à ce Curvy Copter III on comprend maintenant mieux la parité du Square-1, mais c'est une autre histoire, revenons à nos moutons.
Pour commencer, regardons les 4 fig ci-dessous ...

I. état résolu ===>	II. forme non-cubique ===>

III. forme cubique ===>	IV. état résolu

... Et suivons le scénario suivant:

Le twist dispose des rotations, on désigne alors un certain nombre de rotations que l'on nomme rotations standards ou rotations de base
exemple:

• Pour le Rubik's Cube c'est {H,B,A,P,G,D} on ne prend pas h,d,a et les pièces étudiées: sommets, arêtes (pas les centres)
• Pour le Void Cube c'est {H,h,a,P,G,D} on ne prend pas B,A et les pièces étudiées: sommets, arêtes
• Pour le Pyraminx c'est {G,D,H,P,g,d,h,p} les pièces étudiées: sommet, arêtes (pas les centres)
• Pour le Square-1, {3,3B,S,Q,R,T} on ne prend pas {1,B,/} ; et les pièces étudiées: sommets, arêtes (pas l' équateur)
• Pour nous le Curvy Copter III, c'est {A, P, G, D, B, H, O, E, C, T, N, S} , on ne prend pas les rotations non-standards: a,p,g,d,b,... et les pièces étudiées: sommets, feuilles, pétales, centres (pas les arêtes)

à partir des rotations de base on examine s'il y existe des lois de parité du genre:
==> sig(sommets) = sig(centres) = sig(pétales)
==> sig(feuilles) = 1
==> sig(sommets) = dir(arêtes)
....

Si on mélange le Cube uniquement par des rotations de base, la résolution est sans problème. Car les rotations de base gardent le Twist sous la forme cubique et maintiennent les sommets et les arrêtes en phase

Par contre si on a utilisé des rotations non-standard, le Twist change de forme, et quand il revient à la forme cubique les sommets et les arêtes ne sont plus peut-être en phase ! donc à cet état si les sommets et les arêtes ne sont plus en phase on a violé la loi de parité et la résolution conduit au problème de parité.

[1]

Accueil

DMJ: 26/09/2024