Le 2-Super Star Prism

Difficulté: 2.5/20 facile-

1- Notation

Les notations sont comme dans le Square-1, notation additive '+'

Les rotations
Une rotation = une pièce (60° dans le sens horaire)
exemple: 3 - 2B + / = 3-2B/
3 = tourner 3 pièces (3 x 60°) de la face Haut dans le sens des aiguilles d'une montre.
-2B = tourner 2 pièces de la face Bas dans le sens contraire.
/ = slash = tourner 180° la moitié Droite

Les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!
Au lieu d'écrire 1+/+1+(-B)+/+(-2)+/ on écrit simplement 1/1-B/-2/
Rappel 1+/ ≠ /+1

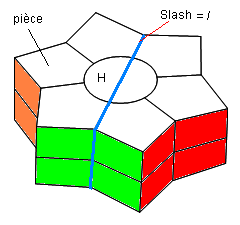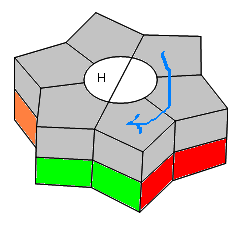Exemple de rotation: 1/1-B/-2/	Rotation H

2- La résolution

La résolution se fait en 2 phases

1. Isoler les sommets
A. On commençe par finir la moitié Haut-gauche avec la formule: /-1/1
B. Puis on place les 3 autres pièces suivant le cas:
* Une pièce à monter: /
* Deux pièces à monter: /1+3B/

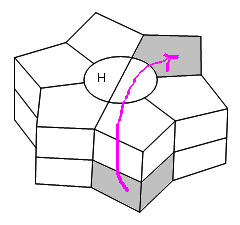/-1/1

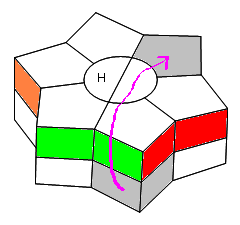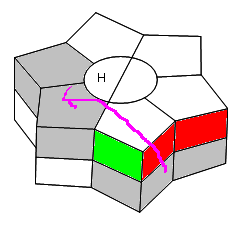Reste 1 pièce à monter: /	Reste 2 pièces à monter: /1+3B/

2. Finir le Bas
Une seule formule ça suffit pour s'en sortir !!!
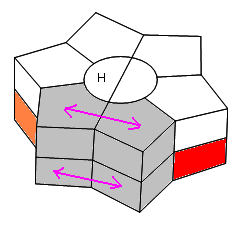
Permuter 2 sommets Bas (et aussi 2 Haut mais on s'en fiche le Haut pour l'instance!):
K = /-1/1+B/-B/

Permuter 2 sommets Haut (2 Bas): K = /-1/1+B/-B/

3. Finir le Haut
Utiliser la même formule pour permuter les sommets Haut: K = /-1/1+B/-B/ mais cette fois ci, il faut toujours appliquer 2 fois (car on perturbe le Bas)
Donc surtout ne bougez pas le Bas !!!

3- Les états singuliers

Le 2-Super Star Prism produit 2 singularités

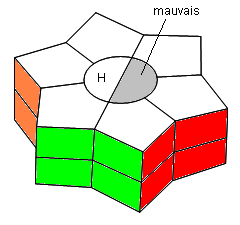
Singularité demi-vis
Placez la mauvaise demi-vis à droite puis faites: /3/3/

/3/3/

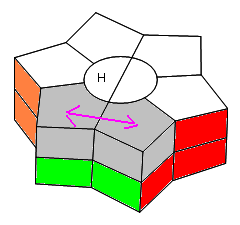
Singularité sommets
Permuter 2 sommets Haut: appliquez 4 fois la formule 1+(/-1/1+B/-B/) c'est à dire
(1+K)+(1+K)+(1+K)+(1+K) = 4(1+K)

4(1+K)	Et voilà !!!

[1]

Accueil

DMJ: 27/12/2024