Floppy Cube
 Inventeurs: Katsuhiko Okamoto
Inventeurs: Katsuhiko Okamoto
Année: 2006 (Premier prix du Puzzle Design Competition 2006)
Nombre d'états: 4!.24/2 = 192
* 4 sommets qui baladent partout ==> 4!
* 4 arêtes à 2 orientations ==> 24
* sig(sommets) = (-1)k ;k=nombre d'orientations arêtes (180°) ==> /2
Ce puzzle inventé par Katsuhiko Okamoto en 2006, a gagné le prix de PDC (Puzzle Design Competition) ! .
C'est un Rubik's Cube de type 3x3x1, il NE CHANGE PAS de forme et il dispose uniquement les 4 rotations de base {A²,P²,G²,D²} et rien d'autres . Mais le mécamisme interne de rotations (le core) tord les centres !!
NOTE: Ce puzzle a gagné le premier prix du PDC 2006 alors que le Mirror Block n'a emporté aucun prix !!! Il faut dire que le jury a un esprit 'louche' et 'tordu' !!!
Le Floppy Cube
| Difficulté: 1/20 facile- | ||||||
|
|
||||||
28
Sept
2013
Commentaire
 |
 |
| Floppy Cube (ne change pas de forme) | Floppy Cube tord les centres |
Il fallait attendre 4 ans plus tard pour avoir un core correct: le Scramble Cube (les centres ne se tordent plus). Ne pas confondre le Scramble Cube avec le Super Floppy, le Super Floppy possède d'autres rotations que les rotations de base
* Floppy Cube : {A²,P²,G²,D²} ne change pas de forme, tord les centres
* Scramble Cube : {A²,P²,G²,D²} ne change pas de forme, ne tord pas les centres
* Super Floppy :{A²,P²,G²,D²} et rotation 90° une arête toute seule (4 orientations) , rotation 90° 1sommet+1arête (change de forme)
En resumé: Si vous voulez un 3x3x1 achetez le Srcamble Cube ignorez les autres.
 |
 |
| Scramble Cube (ne change pas de forme) | Super Floppy: Puzzle Design Competition 2009, le grand prix (change de forme) |
On voit la différence entres les centres.
1- Notation
On va nommer les faces et fixer le Cube:H(aut)=b(lanc), B(as)=j(aune), A(vant)=v(ert), P(ostérieur)=k(lein), G(auche)=o(range), D(roite)=r(ouge)
Les rotations
A = tourner 90° dans le sens horaire
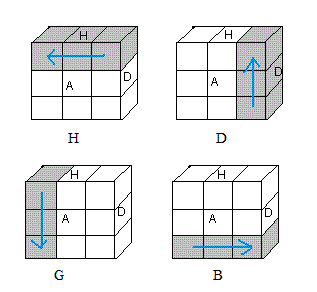 |
|
2- La résolution
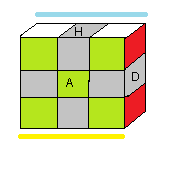
La résolution est très simlpe. On commence par placer les sommets (finir le contour) par les rotations de base : A²,P²,G²,D²les sommets sont répérés par les arêtes adjacentes
puis pivoter les 2 arêtes grâce à la formule: (A²D²) 3
 |
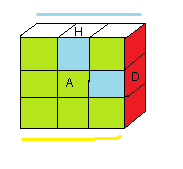 |
| Placer les sommets (finir le contour) | (A²D²) 3 |
[1]
Accueil
DMJ: 05/05/2025


