L'algorithme théorique

Le groupe étendu G⁺ du Rubik's Cube est
G⁺ = (S₁₂ x Z₂¹²) x (S₈ x Z₃⁸)

ceci montre que G⁺ comporte 4 composants (4 morceaux) divisant en deux clans: le clan des arêtes (S₁₂ x Z₂¹²) et le clan des sommets (S₈ x Z₃⁸) , chaque clan comporte 2 morceaux: permutations présenté par S, orientations présenté par Z.

Ceci suggère qu'on a 4 étapes de résolution :

1. Placer les arêts
2. Orienter les arêts
3. Placer les sommets
4. Orienter les sommets

à chaqu'étape de résolution (1),(2),... on n'utilise que des formules dans N et les oppérations (a).

Les 4 formules

L'idée c'est d' avoir 4 formules pour les 4 étapes de la résolutions. Avec le programme Cube Explorer (cube514qtm.exe) on trouve les 4 formules suivantes, qui permettent de restaurer le Cube.
L'ensemble N contient donc 4 formules

Alg0(4)
1. (HG)<->(HP) = GH'GH PB'PBP² GPG'P'G' (minimale)
2. (HG)°(HP)° = PH'P'D'A'G'HP' HPG ADH' (minimale)
3. (HGP)->(HAG)->(HPD) = GAD'A'G'ADA' (minimale)
4. (HGP)^- (HAG)⁺ = AHG AG'PGA' G'H'A'HP'H' (minimale)

En (1) comme c'est un 2-cycle d'arêtes, on peut placer (sous entendu avec les conjugaisons bien sûr) toutes les arêtes.
La loi des flips dit qu'on pivote toujours 2 arêtes donc en (2) on peut pivoter toutes les arêtes
à l'étape (3) , toutes les arêtes sont bien placées, les sommets sont alors en état pair (loi de parité) on peut donc placer tous les sommets avec le 3-cycle-sommet
La loi des twists dit qu'on pivote toujours 2 sommets opposés, ou 3 sommets dans le même sens, donc en (4) on peut pivoter tous les sommets

On a donc un algorithme à 4 formules

Ces formules sont minimales mais n'ont aucune structure !! on ne comprend rien ce que fait la formule !!! et il est difficile de se souvenir .

Première réduction
On peut réduire N, en utilisant K

K = GH'P H'G'H' GHP' H2G'H' = (HG,HP)(HGP,HAG)

On place les arêtes par K, puis on utilise ce même K pour placer les sommets, ce qui est possible parce qu'une fois les arêtes sont bien placées , on aura un nombre pair de couples de sommets à placer (loi de parité) donc on ne dérange pas les arêtes qui sont déjà bien placées.

Alg1(3)
1. (HG)<->(HP) = K
2. (HGP)<->(HAG) = K
3. (HG)°(HP)° = PH'P'D'A'G'HP' HPG ADH' (minimale)
4. (HGP)^- (HAG)⁺ = AHG AG'PGA' G'H'A'HP'H' (minimale)

Algorithme à 3 formules .

Deuxième réduction
On voit que les deux dernières lignes pivotent les pièces, on se demande si on peut les remplacer par une seule formule ? la réponse est affirmative, en effet on pivote 2 fois une arête on revient à son état initial, par contre il faut pivoter 3 fois un sommet pour revenir à son état initial, donc si on trouve une formule qui pivote 2 arêtes et 2 sommets on aura gagné, en voici une :

S = P'D²ADA'HDPG²A'G'AH'G'
= (HG)°(HP)°(HGP)⁺(HAG)^-

Alg2(2)
1. (HG)<->(HP) = K
2. (HGP)<->(HAG) = K
3. (HG)°(HP)° = S
4. (HGP)⁺(HAG)^- = S²

Algorithme à 2 formules !! C'est vraiment pas mal mais on se demande si on peut faire mieux ? càd trouver un algorithme à une seule formule ??
et puis si on peut rendre les formules plus compréhensives ? plus structurées ?? la réponse est "oui" .

Le crochet [DH]

Le problème de ces algorithmes c'est qu'ils utilisent des formules qui n'ont aucune structure, on ne voit rien ce que fait la formule, et il est difficile de les mémoriser.

On voudrait avoir des formules qui soient plus structurées pour comprendre ce qui se passe, ce que fait la formule ... et plus facile à se souvenir .

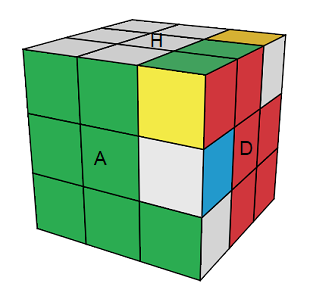
Observons bien ce que fait ce commutateur. [DH] agit sur le Cube comme une sorte de 'Z' et nous le notons Z = [DH]

[DH]

[DH] agit sur le Cube:
Arêtes: (AD)->(HD)->(HP) = (AD,HD,HP) notation moins lourde !
Sommets: (HDA)<->(BAD).(HPD)<->(HGP) = (HDA,BAD)(HPD,HGP)
[DH] = (AD)->(HD)->(HP) . (HDA)<->(BAD).(HPD)<->(HGP)
[DH] = (AD,HD,HP)(HDA,BAD)(HPD,HGP)

Nous allons construire un algorithme autour du commutateur [DH]. c'est-à-dire chaque ligne de l'algorithme doit apparaitre le crochet [DH].
L'idée c'est d'avoir 4 formules qui correspondent aux 4 étapes de la résolution :

Et voilà, si on observe bien on a tout ce qui faut!!!

à partir de [DH] si on veut que tout se passe sur la face Haut il suffit de conjuguer [DH] avec A càd prendre O=A[DH]A' c'est plus clair et plus propre.
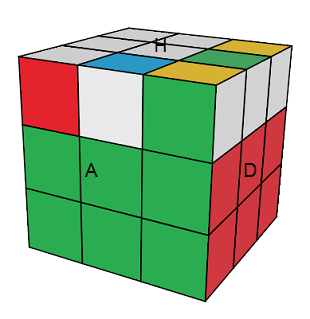
O=A[DH]A' déplace donc 3 arêtes de face Haut

(HP)->(HA)->(HD) = A[DH]A'

Pour orienter les arêtes il suffit de bien observer O=A[DH]A', O laisse une seule bonne arête, on ramène la 2ème bonne arête par H, car on veut seulement avoir 2 mauvaises arêtes c'est-à-dire on prend A[DH]A'.H = J .
Soient a,b,c trois arêtes, et "===>" signifie "appliquer J"
Alors J permute 2 arêtes : a,b, c ===> b°,a, c°
et J² pivote 2 arêtes , en effet :
a,b, c ===> b°,a, c° ===> a°,b° , c°°=c
On a bien pivoté deux arrêtes a,b
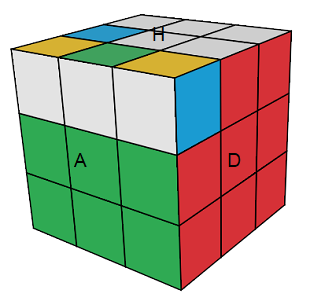
On va prendre J = A[DH]A'.H pour placer les arêtes et J² pour pivoter les arêtes.

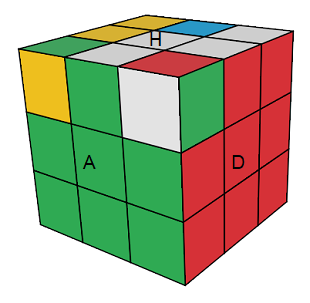J = A[DH]A'.H	(HG)°(HP)° = (A[DH]A'.H)²

NOTE: La formule J permute 2 arêtes et 2 sommets J = (HG,HP)(HGP,HDA)

Voyons maintenant pour les sommets

[DH] modifie une seule pièce de la face G, il échange le sommet (HGP) de la face G, avec (HPD) un autre sommet du Cube, on peut facilement fabriquer un 3-cycle-sommets comme ceci:
[[DH],G] = [DH] .G'[HD]G = (HGP)->(HAG)->(HPD)
Q = [DH] .G'[HD]G (10)

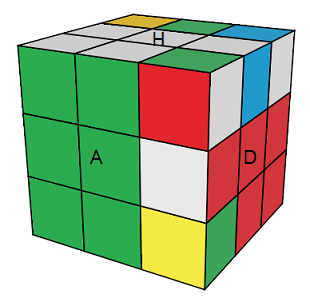
Pour orienter les sommets , obsevons [DH]²:

[DH]²

[DH]² modifie une seule pièce de la face G, il pivote le sommet (HGP) de la face G, il suffit de placer le sommet (HAG) en (HGP) et appliquer l'inverse de ([DH]²)'=[HD]² pour pivoter 2 sommets :
[[DH]²,G] = [DH]² .G'[HD]²G = (HGP)°(HAG)°
T = [DH]² .G'[HD]²G (18)

On a donc N = {J, Q, T}
Et l'algorithme Alg3(3) associé:

1. (HG)<->(HP) = J
2. (HG)°(HP)° = J²
3. (HGP)->(HAG)->(HPD) = Q
4. (HGP)^-(HAG)⁺ = T

à l'étape (3) c'est possible car les arêtes sont bien placeés donc les états des sommets est pair, on peut tous les placer par un 3-cycle.
Les formules sont beaucoups plus claires et structurées donc facile à mémoriser et on voit ce que fait une formule et elles sont construites autour de [DH]

Remarque : on peut remplacer (3) et (4) par (3') et (4') et gagne 2+4=6 rotations mais les formules sont difficiles à retenir.
3'. (HGP)->(HAG)->(HPD) = GAD'A'G'ADA' (8*)
4'. (HGP)^- (HAG)⁺ = AHGAG'PGA'G'H'A'HP'H' (14*)

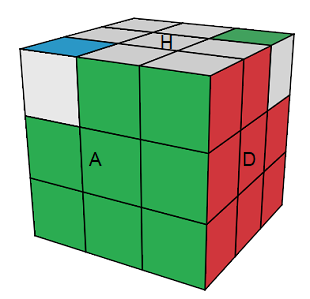
(HP)->(HA)->(HD) = A[DH]A'	(HG)°(HP)° = (A[DH]A'.H)²

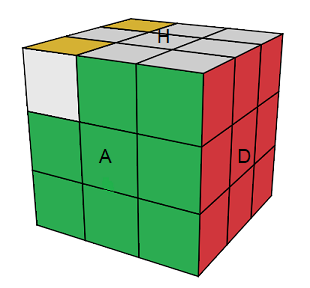(HGP)->(HAG)->(HPD) = [DH] .G'[HD]G	(HGP)- (HAG)+ = [DH]² .G'[HD]²G

Remarque : A partir de J, Q, T on peut adapter pour avoir un algorithme de résolution tout à fait raisonnable, c'est ce que j'ai fait:

1. Placer les arêtes
   * Bas: (HA)->(BA) = A²
   * Equateur: (HP)->(AD) = [DH]
   * Haut: (HG)<->(HP) = A[DH]A'H
2. Pivoter les arêtes: (HG)°(HP)° = (A[DH]A'.H)²
3. Placer les sommets: (HGP)->(HAG)->(HPD) = [DH] .G'[HD]G
4. Pivoter les sommets: (HGP)^-(HAG)⁺ = [DH]² .G'[HD]²G

L'algorithme [DH]

(HG)<->(HP) = A[DH]A'H
(HG)°(HP)° = (A[DH]A'H)²
(HGP)->(HAG)->(HPD) = [DH] G'[HD]G
(HGP)^-(HAG)⁺ = [DH]² G'[HD]²G

On dira aussi les 4 équations de la restauration.
Voilà, on remonte le Cube avec un algorithme construit autour du commutateur [DH], chaque ligne on voit apparaitre [DH]:
¤ Un principe simple à comprendre: On place les arêtes puis les oriente. On place des sommets puis les oriente.
¤ 3 formules
¤ Les formules sont structurées donc facile à comprendre et facile à mémoriser

L'algorithme théorique

On a trouvé un algorithme structuré à 3 formules, récemment j'ai apperçu qu'on peut encore aller plus loin...
La formule J = A[DH]A'H est vraiment intéressante, on effet :

1. J permute 2 arêtes et 2 sommets
2. J² (ou J⁶) pivote 2 arêtes
3. J⁴ pivote 3 sommets

J permute 2 arêtes et 2 sommets, on se demande si on peut l'utiliser pour placer les pièces ?
à priori non, en effet J permute 2 arêtes et 2 sommets donc soit on l'utilise pour placer les arêtes, soit on l'utilise pour placer les sommets. Une fois utilisé J pour placer les arêtes par ex, si on utilise J une deuxième fois pour placer les sommets on pertubera les arêtes !!!

Mais le Rubik's Cube possède une loi qui va nous sauver la vie! la loi des phases. La loi des phases dit "les sommets et les arêtes sont en phases" c'est-à-dire sig(u)=sig(v) . Autrement dit quand toutes les arêtes sont bien placées, on aura un nombre pair de couples de sommets à placer donc on ne perturbe pas les arêtes.

* On commence par placer toutes les arêtes par J
* Après avoir placer toutes les arêtes, on place alors les sommets grâce à J aussi ! on place (HGP)->(HDA) (avec la conjugaison) en veillant de ne pas toucher les arêtes (HG) et (HP) c'est-à-dire ne pas utiliser les rotations H, G et P, c'est possible parce que les sommets sont maintenant en état pair (sig(u)=1=sig(v)).
* On pivote les arêtes par J² (ou J⁶),
* on pivote les sommets par J⁴

Alléluia !! une seule formule pour restaurer le Cube !!! ...

N = {J = A[DH]A'.H}
Et l'algorithme Alg4(1) associé:

• (HG)<->(HP) = J = A[DH]A'.H
• (HGP)<->(HDA) = J = A[DH]A'.H
• (HG)⁺(HP)⁺ = J² = (A[DH]A'.H)² (ou J⁶)
• (HGP)⁺(HAG)⁺(HDA)⁺ = J⁴ = (A[DH]A'.H)⁴

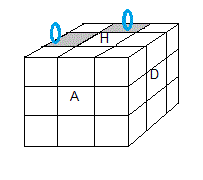
(HG)<->(HP) = A[DH]A'.H	(HGP)<->(HDA) = A[DH]A'.H

(HG)+(HP)+ = (A[DH]A'.H)2	(HGP)+(HAG)+(HDA)+ = (A[DH]A'.H)4

NOTE: à l'étape (2) , voici quelques formules pour vous aider à placer les sommets Haut

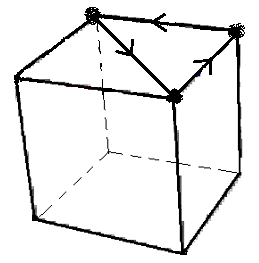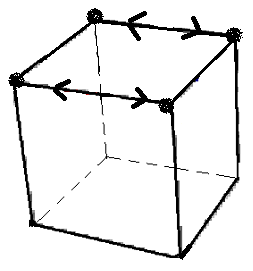un 3-cycle: (HDA)->(HPD)->(HGP) = [JD']	Dans ce cas appliquer D'JD .J pour avoir un 3-cycle

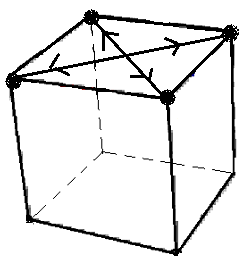Dans ce cas appliquer J .D'JD pour avoir un 3-cycle

Et voilà, il est vraiment extraordinaire qu'on puisse restaurer le Cube avec seulement une formule construite autour d'un seul commutateur [DH] !! C'est incroyable n'est ce pas ?

Cet algorithme en pratique n'est pas vraiment utilisable mais en théorie il peut être très utile, par ex on peut programmer un Robot pour résoudre le Cube, à part l'algorithme, il faut stocker les formules en mémoire, donc si la mémoire coûte chère on peut faire des économies en utilisant l'agorithme théorique avec une seule formule à stocker.

REMARQUE : J⁴ et J⁶ sont propres donc indépendants (l'ordre d'exécution n'intervient pas)

Donc l'algorithme théorique est par définition :

• Placer les arêtes : Q
• Placer les sommets : Q
• Pivoter les arêtes : Q²
• Pivoter les sommets : Q⁴

où Q est une formule , la formule Q dans l'algorithme théorique est nommée formule première.

Finalement on a 4 équations pour restaurer le Cube , ces équations n'utilise qu'une seule formule J

• (HG)<->(HP) = J
• (HGP)<->(HDA) = J
• (HG)⁺(HP)⁺ = J²
• (HGP)⁺(HAG)⁺(HDA)⁺ = J⁴

Il est vraiment frappant qu'il y a une analogie avec les 4 équations de Maxwell en électromagnétique

• div(B) = 0
• rot(E) = - ∂B/∂t
• div(E) = p/ε
• rot(B) = µj + εµ∂E/∂t

NOTE : On pourrait dire que J et Z , 2 constances de la structures M, et elles sont reliés par
J = Z^A H

1 2 [3] 4 5 6

Accueil

DMJ: 18/09/2024