Méthode de Thistlethwaite

Le nombre minimum de rotations

Un raisonement simple permet de trouver qu'il y a des états qu'on ne peut pas s'en sortir avec 19 rotations (a=20)

- Le 1er coup : 6 faces à choisir {H,B,A,P,G,D} , on prend par ex la face A, on a alors 2 choix : A, A' et comme il y a 6 faces on a: 2x6=12 choix.
A: A,A' ⇒ 2x6 = 12

- Le 2ème coup : on évite de reprendre la face A sinon on risque de revenir au même point, donc 5 faces à choisir {H,B,P,G,D} ,on prend par ex la face D
D: D,D' ⇒ 2 x 5 = 10, comme on a 12 choix au 1ème coup d'où
12 x 10

- Le 3ème coup : on évite de reprendre la face D sinon on risque de revenir au même point, mais on peut reprendre la face A car D a modifié la face A, on ne revient pas au même point si on reprend la face A, donc 5 faces à choisir {H,B,A,P,G} , on prend par ex P
P: P,P' ⇒ 2 x 5 = 10, mais on a 12x10 choix d'où
12 x 10 x 10

- Le 4ème coup : on évite de reprendre la face P, donc 5 faces à choisir {H,B,A,G,D} , on prend par ex la face H
H: H,H' ⇒ 2 x 5 = 10,
mais on a maintenant 12x10x10 choix d'où
12 x 10x10x10
......

Le nombre d'états en n rotations vaut donc:
S = 12 + 12.10 + 12.10² + 12.10³ + ... + 12.10^n-1 ;(il y a n ternes)
S = 12(1 + 10 +10² +10³+ ... +10^n-1)
S = 12(10ⁿ - 1)/(10 - 1) ≈ 4.10ⁿ/3
10ⁿ ≈ 3x4,3x10¹⁹/4
10ⁿ ≈ 3,22x10¹⁹
En passant par ln
n ≈ [ln(3,22)+19ln(10)]/ln(10)
n ≈ 19,50
d'où
n = 20

la borne inférieure est donc a = 20 autrement dit il existe des états dont on n'a aucun espoir de les restaurer avec 19 rotations !
on a 20 ≤ m ≤ b

Analyse

Pour trouver le majorant b, Thistlethwaite a une idée géniale suivante:

On a d'un côté (M, .) le groupe des formules, et de l'autre côté (G, .) le groupe du Rubik's Cube, le groupe des états.
Si on se donne une tour {H_i}_i de sous groupes de M
M = H₀ ⊃ H₁ ⊃ H₂ ⊃ ... ⊃ H_n = {I}
à cette tour il correspond à une tour {E_i}_i de sous ensembles de G
G = E₀ ⊃ E₁ ⊃ E₂ ⊃ ... ⊃ E_n = {e}
où les E_i sont des états atteints par les H_i , E_i = { s | s=e•V, V∈H_i }
Ainsi on a donc un algorithme de résolution (on part de G et on arrive à {e}), on pourrait alors calculer le nombre de rotations utilisées dans cet algorithme donc un majorant b de m.

Les classes

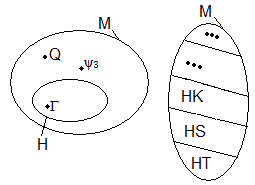
Pour comprendre l'idée de Thistlethwaite, càd comment il compte le nombre de rotations, il faut connaître la notion de classes. Thistlethwaite a utilié les classes pour compter les rotations c'est vraiment génial comme l'angle d'attaque.

Pour fixer les idées on va prendre simplement une tour à un étage :
Soit H un sous-groupe de M (H n'est pas forcement normal) et E les états atteints par H
H ⊂ M, et E ⊂ G
H étant donné, les classes H\M = { HK, HS, HT, ... } où les K, S, T, ... (dans M) sont, donc aussi données . Soient s un état quelconque de G et Q la formule associée à s : e•Q = s ∈ G


Une classe a un nombre fini d'éléments (puisque M est fini -c'est ici donc qu'on a besoin que M soit fini-), parmi ces éléments il y a un "plus court" , et on peut prendre ce "plus court" comme représentant de la classe.
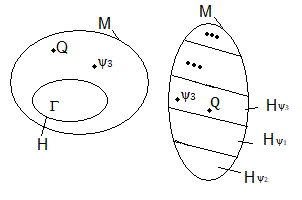
Soient: HK = Hψ₁, HS = Hψ₂, HT = Hψ₃, ... où les ψ_i∈M et sont des plus courtes et |ψ_i|=longueur
on pose
L = Max {|ψ₁|, |ψ₂|, |ψ₃|, ...}

Q étant un élément de M , mais comme les classes forment une partition de M donc Q se trouve quelque part dans Hψ₁, ou Hψ₂, ou Hψ₃, ...
supposons que Q soit dans Hψ₃ ça signifie:
Q = Γψ₃ avec Γ∈H
d'où

Q = Γψ₃
Qψ'₃ = Γ
e•(Qψ'₃) = e•Γ
(e•Q)•ψ'₃ = e•Γ
s•ψ'₃ = e•Γ = t ∈E , car Γ est dans H
d'où:
s•ψ'₃ = t ∈E

Donc on passe de l'état s à l'état t au maximum L rotations.

NOTE Il est clair qu'on ne cherche pas les ψ_i à la main !!! , les ordinateurs sont là pour ça ...
En effet le nombre d'éléments d'une classe est fini, souvenez vous il vaut |H|. Donc on peut très bien faire un programme qui cherche le plus court élément ψ d'une classe. Pour trouver L là aussi il y a un nombre fini de classes (de ψ_i) , il vaut |M|/|H| donc on peut toujours trouver
L = Max {|ψ₁|, |ψ₂|, |ψ₃|, ...} par ordinateur. Donc H est donné , L est donné.

Méthode de Thistlethwaite

Dans cette section on applique le couple (M,H) par les couples (H_i,H_i+1)
Thistlethwaite a proposé la suite H_i des sous groupes de M suivantes :
H₀ = M = < H, B, A, P, G, D > ==> E₀ = G
H₁ = < H, B, A², P², G, D > ==> E₁
H₂ = < H, B, A², P², G², D² > ==> E₂
H₃ = < H², B², A², P², G², D² > ==> E₃
H₄ = {I} ==> E₄ = {e}

Et il utilisait un programme informatique qui charchait les longueurs et il trouvait que pour passer :
¤ de E₀ = G à E₁, il y a 2048 ψ_i et le maxi |ψ_i|=14 , càd L=14
¤ de E₁ à E₂, il y a 1082565 ψ_i et le maxi |ψ_i|=26 , càd L=26
¤ de E₂ à E₃, il y a 29400 ψ_i et le maxi |ψ_i|=30 , càd L=30
¤ de E₃ à E₄, il y a 663552 ψ_i et le maxi |ψ_i|=34 , càd L=34

Soit au total b=104 rotations , 20 ≤ m ≤ 104
NOTE: Avec quelques astuces on arrive à diminuer b=90 (14+20+26+30) .

D'après le diagrame de marquages
H₁ signifie : toutes les arêtes sont bien orientées
H₂ signifie : toutes les arêtes et les sommets sont bien orientées

==> Passer de E₀ = G à E₁ signifie : à partir de l'état s∈G il existe une formule V∈M , |V|≤14 telle que s•V=s₁ ∈E₁
==> Passer de E₁ à E₂ signifie : à partir de l'état s₁∈E₁ il existe une formule V₁∈H₁ , |V₁|≤26 telle que s₁•V₁=s₂ ∈E₂
==> Passer de E₂ à E₃ signifie : à partir de l'état s₂∈E₂ il existe une formule V₂∈H₂ , |V₂|≤30 telle que s₂•V₂=s₃ ∈E₃
==> Passer de E₃ à E₄ signifie : à partir de l'état s₃∈E₃ il existe une formule V₃∈H₃ , |V₃|≤34 telle que s₃•V₃=s₄ = e ∈E₄

Remarque : Le travail Thistlethwaite est important, il nous dit deux choses:
1. On est sûr de s'en sortir !!.
2. Quel que soit l'état du Cube on peut le restaurer au maximum 104 rotations.

Durant les années on augmente le minorant a et on diminue le majorant b

Janvier, 1981 : Dan Hoey montre que : 21 ≤ m ≤ 140
Juillet, 1981 : Morwen Thistlethwaite montre que : 21 ≤ m ≤ 104
Mai, 1992 : Michael Reid montre que : 21 ≤ m ≤ 56
Janvier, 1995 : Michael Reid, 21 ≤ m ≤ 42
Janvier, 1995 : Michael Reid, 22 ≤ m ≤ 42
Août, 1998 : Michael Reid a trouvé le SuperFlip a=24, 24 ≤ m ≤ 42
Août, 1998 : Michael Reid a trouvé le SuperFlip4Spot a=26, 26 ≤ m ≤ 42
Novembre, 2005 : Silviu Radu, 26 ≤ m ≤ 40
Janvier, 2006 : Bruce Norskog, 26 ≤ m ≤ 38
Janvier, 2006 : Silviu Radu, 26 ≤ m ≤ 36
Mars, 2006 : Silviu Radu, 26 ≤ m ≤ 35
Juillet, 2007 : Silviu Radu, 26 ≤ m ≤ 34
Janvier, 2009 : Tomas Rokicki, 26 ≤ m ≤ 32
Janvier, 2009 : Tomas Rokicki, 26 ≤ m ≤ 31
Février, 2009 : Tomas Rokicki, 26 ≤ m ≤ 30
Juin, 2009 : Tomas Rokicki, 26 ≤ m ≤ 29
Finalement Août, 2014 : Tomas Rokicki et Morley Davidson démontrent que b=26, 26 ≤ m ≤ 26

Théorème (Tomas Rokicki, Morley Davidson 2014): quel que soit l'état s, il existe une formule V avec |V|≤26 telle que s•V=e
Autrement dit le diamètre du Rubik's Cube est 26. huuff !! 33 ans de galère !!...

Le SuperFlip de formule
Φ = D'H²PG'AH'PBAHB'GB²A'DP'BA'H'P'HB'
(Mike Reid trouvé par ordinateur, plus courte formule |Φ|=24)
Le SuperFlip4Spot de formule
Π = H²B²GA²H'BD²PH'B'DGA²DHB'D'GHA'P'
(Mike Reid trouvé par ordinateur, prouvé par Mike Reid plus courte formule 26)
Π = ADG'PBAD'HBPD'B'D'PH²B²P²DGB²DG (minimale)
c'est le seul état SuperLoin (antipode) que l'on connait.

|Φ|=24
|Π|=26
Le diamètre du Rubik's Cube est: 26

Remarques

Parfois on compte |A²|=1 on dit qu'on utilise la métrique face-rotation et on note avec un 'f' :
ex: |H| = 1f, |H'| = 1f, |H²| = 1f, |I| = 0f
V = HB²PA'D³G'²
|V| = 7f
Dans ce cas on démontre que le diamètre du Rubik's Cube vaut 20f

Théorème (Tomas Rokicki, Herbert Kociemba, Morley Davidson, et John Dethridge, 2010): quel que soit l'état s, il existe une formule V avec |V|≤20f telle que s•V=e

Voici quelques états les SuperLoin en f-rotation (20f, antipodes)
Le SuperFlip dont la formule est
Φ = AH'A²B'PHD'A'GB'D'H'GHP'B²D'AH²B² (|Φ|=20f)
X = DGH²AH'BA²D²P²GH²A'P'HD²BA²HD²H
Y = AH'A²B'PHD'A'GB'D'H'GHP'B²D'AH²B²
Il y a environ 490.000.000 états SuperLoin en f-rotation

|Φ|=20f
|Π|=20f

L'Agorithme de Thistlethwaite pour un Humain

ATH

1 2 3 4 5 6 [7] 8

Accueil

DMJ: 11/09/2024