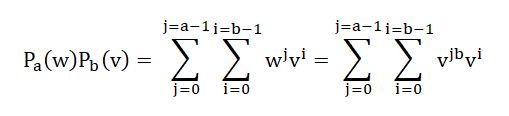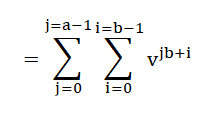L'ordre maximal d'un élément de G
7
Mars
2014
Préface
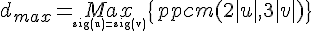 Auteur: morphocode
Auteur: morphocode
Année: 2014
Le but de cet article c'est démontrer mathématiquement l'ordre maximal dmax d'un élément de G (ou l'ordre maximal d'une formule) est 1260
Beaucoup de gens en parlent , mais souvent c'est vague, pas de démontration et on ne sait toujours pas pourquoi ça vaut 1260.
Il existe des algorithmes qui calculent tous les ordres de G, et on trouve évidemment le plus grand c'est 1260
Mais ce qu'on veut c'est une démontration mathématique ...
Définitions et notations
Rappel
G
+ = S
12 x Z
212 x S
8 x Z
38 le groupe étendu de G
Le groupe du Rubik's Cube G est l'ensemble des éléments (u,x,v,y) de G
+ vérifiant:
1. ∑ x
i = 0 (mod 2) où x = (x
1,x
2,...,x
12)
2. ∑ y
i = 0 (mod 3) où y = (y
1,y
2,...,y
8)
3. sig(u)=sig(v)
L'ordre
L'ordre d'une permutation v , c'est le plus petit entier positive d tel que v
d = 1 (ici 1 représente l'identité=id) et on le note |v| = d
NOTE Si v est composé de cycles disjoints son ordre vaut le ppcm des cycles
v = (a-cycle)(b-cycle)(c-cycle)
alors
|v| = d = ppcm(a,b,c)
Théorème central:
On pose:
m=ppcm(a,b) et
A = {m'=ppcm(a',b') avec a'|a et b'|b}
B = {k / k|m }
Aors A=B
Div(m) = {ppcm(Div(a), Div(b))} , Div(a)=l'ensemble des diviseurs de a
Démontration
On va raisonner sur un exemple.
a=p
3 q
2
b=p
2 r
3
Div(a)={ (1+p+p²+p
3)(1+q+q²) } = {a'=p
i q
j ; 0≤i≤3, 0≤j≤2 }
Div(b)={ (1+p+p²)(1+r+r²+r
3) } = {b'=p
k r
t ; 0≤k≤2, 0≤t≤3 }
m=ppcm(a,b)= p
3 q
2 r
3 ; tout et plus grande puissance
Div(m) = {(1+p+p²+p
3)(1+q+q²)(1+r+r²+r
3) }= {x=p
f q
g r
h ; 0≤f≤3, 0≤g≤2 , 0≤h≤3 }
a' = p
i q
j , a'∈Div(a)
b' = p
k r
t , b'∈Div(b)
m'=ppcm(a',b') = p
i q
j r
t en supposant que i absorbe k, k < i
et x=p
f q
g r
h un divideur de m, on voit que m'=p
i q
j r
t et x ont de la même forme, et les puissances (f,g,h),(i,j,t)
varient de la même façon donc ces deux ensembles sont égaux A=B
m'∈A ⇒ m'=ppcm(a',b')=p
i q
j r
t , même forme que x donc ⇒ m'∈B ⇒ A ⊂ B
x∈B ⇒ x = p
f q
g r
h, même forme que m' donc x provient d'un ppcm ⇒ x=ppcm(a',b') ⇒ x∈A ⇒ B ⊂ A
finalement A=B
Un sommet est repésenté par, (v,y)∈S
8 x Z
38 et la loi de compsition donne
(v,y)(w,z) = (vw, y + v(z) )
donc pour
(v,y)² = (v², y + v(y) )
(v,y)
3 = (v
3, y + v(y) + v²(y) )
....
(v,y)
b = (v
b, y + v(y) + v²(y) + ...+v
b-1(y) )
par définition on note
y + v(y) + v²(y) + ...+v
b-1(y) = y
b
d'ou
(v,y)
b = (v
b, y
b)
On appelle l'ordre du vecteur y (en v) c'est le plus petit entier positif b tel que
y + v(y) + v²(y) + ...+v
b-1(y) = 0
et on le note |y| = b
Big théorème.
On a le théorème suivant
Théorème
L'ordre du vecteur d'orientation y (en v) est un diviseur de 3|v|
|y| | 3|v|
de même pour les arêtes
L'ordre du vecteur d'orientation x (en u) est un diviseur de 2|u|
|x| | 2|u|
Remarque
3|v| ==> 3 parce qu' un sommet a 3 orientations
2|u| ==> 2 parce qu' une arête a 2 orientations
L'ordre de l'orientation ne dépend que de l'ordre de la permutation
On va faire la démontration pour les sommets (v,y)∈S
8 x Z
38 , pour les arrêtes c'est pareil. Mais avant
on va étudier un polynôme nécessaire à la démontration.
Posons: P
d(v) = 1 + v + v² + ...+v
d-1 un polynôme en v et P
0(v) = 0
Commençons par avoir quelques propriétés de ce polynôme
P1. P
ab(v) = P
a(v
b) P
b(v)
P2. P
ab+r(v) = v
rP
ab(v) + P
r(v)
P3. P
3|v|(v) = 3P
|v|(v)
Démontration P1
Posons w = v
b
P
a(w) = 1 + w + w² + ...+w
a-1
P
b(v) = 1 + v + v² + ...+v
b-1
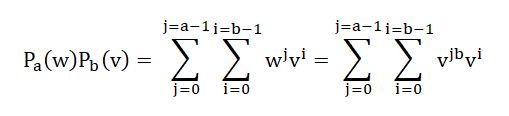
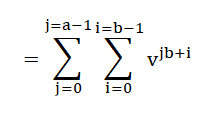
1 + v + v² + ...+ v
b-1
+v
b + v
b+1 +...+ v
2b-1
+v
2b + v
2b+1 +...+ v
3b-1
+v
3b + v
3b+1 +...+ v
4b-1
...
+v
(a-1)b + v
(a-1)b+1 +...+ v
ab-1
= P
ab(v)
Démontration P2
P
ab+r(v) - P
r(v) = v
r + v
r+1 + v
r+2...+ v
ab+r - 1
= v
r(1 + v
+ v
2...+ v
ab-1)
= v
r( P
ab(v) )
Démontration P3
P
3|v|(v) = P
3(v
|v|) P
|v|(v) ; d'après P1
= P
3(1) P
|v|(v) ; car |v| est l'ordre de v
= 3P
|v|(v)
Démontration de théorème
L'ordre du vecteur y est un diviseur de 3|v|
donc soit d = l'ordre de y càd le plus petit entier tel que
y + v(y) + v²(y) + ...+v
d-1(y) = 0 (*)
il faut donc démontrer que d divise 3|v|
on divise 3|v| par d donc 3|v|=kd+r avec 0 ≤ r < d
P
3|v|(v) = P
kd+r(v)
3P
|v|(v) = v
rP
kd(v) + P
r(v)
3P
|v|(v) = v
r( P
k(v
d) P
d(v) ) + P
r(v)
appliquons à y
[3P
|v|(v)](y) = [v
r( P
k(v
d) P
d(v)(y) ) + P
r(v)](y)
[3P
|v|(v)](y) = [P
|v|(v)](3y) = 0 car y∈Z
38
[P
d(v)](y) = 0 car d est l'ordre de y
d'où
[P
r(v)](y) = 0
mails alors comme d est le plus petit entier qui vérifie (*) donc ça force r=0
finalement on a donc
P
3|v|(v) = P
kd+0(v) d'ou 3|v|=kd ca signifie que d divise 3|v|
[1] 2
Accueil
DMJ: 09/03/2022
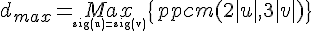 Auteur: morphocode
Auteur: morphocode