L'ordre maximal d'un élément de G

L'ordre dans G⁺

Le but est de montrer l'ordre maximal dans G⁺ est 1260 , puis trouver un élément de G⁺ ayant l'ordre maximal et ensuite montrer qu'il appartient à G

(u,x,v,y)∈G⁺
|(u,x,v,y)| = d = ordre de (u,x,v,y) => (u,x,v,y)^d = (id,0,id,0)
|(u,x)| = p = ordre de (u,x) => (u,x)^p = (id,0)
|u| = t = ordre de u => u^t = id
|x| = a = ordre de x => x^a = x + u(x) + u²(x) + ...+u^a-1(x) = 0

Relation sur les ordres
|(u,x,v,y)| = ppcm(|(u,x)|,|(v,y)|)
|(u,x)| = ppcm(|u|,|x|)
|(v,y)| = ppcm(|v|,|y|)

On a la chaine
(u,x,v,y)^d ⇒ (u,x)^p(v,y)^q ⇒ (u^|u|,x^|x|)(v^|v|,y^|y|)
avec
d = ppcm(p,q)
p = ppcm(|u|,|x|)
q = ppcm(|v|,|y|)

on pose: |x|=a, |y|=b
on note O_u,v les ordres "provenant" de u,v
O_u,v = { d∈N , d = ppcm( ppcm(|u|,a),ppcm(|v|,b) ) où a| 2|u| et b| 3|v| }
et tous les ordres de G⁺ c'est la réunion des O_u,v
O = U O_u,v avec u∈S₁₂ et v∈S₈

Pour avoir un ordre d de G⁺ on fixe u et v puis on fait varier a et b
ensuite on fait varier u et v

NOTE Les ordres ne dépendent que les permutations pas d'orientation

On pose:
m=ppcm(2|u|,2|u|)=2|u|
A = {p=ppcm(|u|,a) avec |u|| 2|u| et a| 2|u| }
B = {k / k|m} = {k / k| 2|u|}

m'=ppcm(3|v|,3|v|)=3|v|
A' = {p'=ppcm(|v|,b) avec |v|| 3|v| et b| 3|v| }
B' = {k' / k'|m'} = {k' / k'| 3|v|}

D'après le théorème central on a A=B, et A'=B' donc on peut remplacer
ppcm(|u|,a) → k
ppcm(|v|,b) → k'
d'où
{ d = ppcm( ppcm(|u|,a),ppcm(|v|,b) ) où a| 2|u| et b| 3|v| }
{ d = ppcm(k,k') où k| 2|u| et k'| 3|v| }
Et on recommence le même raisonnement
On pose:
m=ppcm(2|u|,3|v|)
A = {p=ppcm(k,k') avec k| 2|u| et k'| 3|v| }
B = {h / h|m}

donc ordre d d'un élément de G⁺ est un diviseur de m: d|m
et ordre max dans G⁺ : Max B ⇒ Max {ppcm(2|u|,3|v|)}

d'où le

théorème

l'ordre d d'un élément de G est: d|m où m=ppcm(2|u|,3|v|) avec sig(u)=sig(v)
et
L'ordre maximale d dans G est: d_max = Max {ppcm(2|u|,3|v|)} , avec sig(u)=sig(v)

C'est un ordre dans G⁺ et on ajoute la condition sig(u)=sig(v).
Maintenant il faut trouver u et v avec sig(u)=sig(v) , tels que ppcm(2|u|,3|v|) soit maximal

Partition de 8 et 12

Soit u∈S₁₂ pour calculer l'orde de u , |u|=d il serait plus facile de décomposer u en cycles disjoints alors l'ordre de u c'est le ppcm de l'ordre des cycles
La décomposition de u en cycles disjoints revient à partitionner l'entier 12 , par exp la partition
12 = 5+4+2+1
revient à dire
u = (5-cycle)(4-cycle)(2-cycle)(1-cycle)
et
|u|=ppcm(5,4,2,1)=20

On va donc chercher les partitions de 12 (il y a p(12)=77)

partition paire (donc u est pair)
1. 11+1 ==> 11
2. 10+2 ==> 10
3. 9+3 ==> 9
4. 8+4 ==> 8
5. 7+5 ==> 35
6. 6+6 ==> 6
7. 9+1+1+1 ==> 9
8. 8+2+1+1 ==> 8
9. 7+3+1+1 ==> 21
10. 6+4+1+1 ==> 12
11. 5+5+1+1 ==> 5
12. 7+2+2+1 (*) ==> ppcm(7,2,2,1)=14
13. 6+3+2+1 ==> 6
14. 5+4+2+1 ==> 20
15. 5+3+3+1 ==> 15
16. 4+4+3+1 ==> 12
17. 6+2+2+2 ==> 6
18. 5+3+2+2 ==> 30
19. 4+4+2+2 ==> 4
20. 4+3+3+2 ==> 12
21. 3+3+3+3 ==> 3
22. 7+1+1+1+1+1 ==> 7
23. 6+2+1+1+1+1 ==> 6
24. 5+3+1+1+1+1 ==> 15
25. 4+4+1+1+1+1 ==> 4
26. 5+2+2+1+1+1 ==> 10
27. 4+3+2+1+1+1 ==> 12
28. 3+3+3+1+1+1 ==> 3
29. 4+2+2+2+1+1 ==> 4
30. 3+3+2+2+1+1 ==> 6
31. 3+2+2+2+2+1 ==> 6
32. 2+2+2+2+2+2 ==> 2
33. 5+1+1+1+1+1+1+1 ==> 5
34. 4+2+1+1+1+1+1+1 ==> 4
35. 3+3+1+1+1+1+1+1 ==> 3
36. 3+2+2+1+1+1+1+1 ==> 6
37. 2+2+2+2+1+1+1+1 ==> 2
38. 3+1+1+1+1+1+1+1+1+1 ==> 3
39. 2+2+1+1+1+1+1+1+1+1 ==> 2
40. 1+1+1+1+1+1+1+1+1+1+1+1 ==> 1
P₁₂ = {11,10,9,8,35,6,21,12,5,14,20,15,30,4,3,7,2,1}

partition impaire (donc u est impair)
1. 12 ==> 12
2. 10+1+1 ==> 10
3. 9+2+1 ==> 18
4. 8+3+1 ==> 24
5. 7+4+1 ==> 28
-u 6. 6+5+1 ==> 30
7. 8+2+2 ==> 8
8. 7+3+2 ==> 42
9. 6+4+2 ==> 12
10. 5+5+2 ==> 10
11. 6+3+3 ==> 6
12. 5+4+3 ==> 60
13. 4+4+4 ==> 4
14. 8+1+1+1+1 ==> 8
15. 7+2+1+1+1 ==> 14
16. 6+3+1+1+1 ==> 6
17. 5+4+1+1+1 ==> 20
18. 6+2+2+1+1 ==> 6
19. 5+3+2+1+1 ==> 30
20. 4+4+2+1+1 ==> 4
21. 4+3+3+1+1 ==> 12
22. 5+2+2+2+1 ==> 10
23. 4+3+2+2+1 ==> 12
24. 3+3+3+2+1 ==> 6
25. 4+2+2+2+2 ==> 4
26. 3+3+2+2+2 ==> 6
27. 6+1+1+1+1+1+1 ==> 6
28. 5+2+1+1+1+1+1 ==> 10
29. 4+3+1+1+1+1+1 ==> 12
30. 4+2+2+1+1+1+1 ==> 4
31. 3+3+2+1+1+1+1 ==> 6
32. 3+2+2+2+1+1+1 ==> 6
33. 2+2+2+2+2+1+1 ==> 2
34. 4+1+1+1+1+1+1+1+1 ==> 4
35. 3+2+1+1+1+1+1+1+1 ==> 6
36. 2+2+2+1+1+1+1+1+1 ==> 2
37. 2+1+1+1+1+1+1+1+1+1+1 ==> 2
I₁₂ = {12,10,18,24,28,30,8,42,6,60,4,14,20,2}

De même cherchons les partitions de 8 (il y a p(8)=22)

partition paire (donc v est pair)
1. 7+1 ==> ppcm(7,1)=7
2. 6+2 ==> ppcm(6,2)=6
3. 5+3 (*) ==> ppcm(5,3)=15
4. 4+4 ==> ppcm(4,4)=4
5. 5+1+1+1 ==> ppcm(5,1,1,1)=5
6. 4+2+1+1 ==> ppcm(4,2,1,1)=4
7. 3+3+1+1 ==> 3
8. 3+2+2+1 ==> 6
9. 2+2+2+2 ==> 2
10. 3+1+1+1+1+1 ==> 3
11. 2+2+1+1+1+1 ==> 2
12. 1+1+1+1+1+1+1+1 ==> 1
P₈ = {7,6,15,4,5,3,2,1}

partition impaire (donc v est impair)
1. 8 ==> 8
2. 6+1+1 ==> 6
3. 5+2+1 ==> 10
4. 4+3+1 ==> 12
5. 4+2+2 ==> 4
6. 3+3+2 ==> 6
7. 4+1+1+1+1 ==> 4
8. 3+2+1+1+1 ==> 6
9. 2+2+2+1+1 ==> 2
10. 2+1+1+1+1+1+1 ==> 2
I₈ = {8,6,10,12,4,2}

On va montrer que ces deux partitions (*) donneront la solution de notre problème

L'ordre maximal

On a vu que l'ordre d , d'un élément (u,x,v,y) de G est donné par
d|m où m=ppcm(2|u|,3|v|) avec sig(u)=sig(v)
l'ordre maximal est donc
d_max = Max[ppcm(2|u|,3|v|)] avec sig(u)=sig(v)

On doit trouver u,v avec sig(u)=sig(v) tels que ppcm(2|u|,3|v|) soit maximal
Pour ça on calcule ppcm(2|u|,3|v|), et on prend le plus grand, c'est-à-dire d Max[ppcm(2|u|,3|v|)]

P₁₂ = {11,10,9,8,35,6,21,12,5,14,20,15,30,4,3,7,2,1}
P₈ = {7,6,15,4,5,3,2,1}

I₁₂ = {12,10,18,24,28,30,8,42,6,60,4,14,20,2}
I₈ = {8,6,10,12,4,2}

comme sig(u) = sig(v) on prend donc u,v toutes les deux paires ou impaires
voyons quelques valeurs
u∈I₁₂ , v∈I₈
(30,12) ==> ppcm(2x30,3x12)=180
(18,10) ==> ppcm(2x18,3x10)=180
(12,8) ==> ppcm(2x12,3x8)=24
(42,10) ==> ppcm(2x42,3x10)=420
...
...
u∈P₁₂ , v∈P₈
(7,15) ==> ppcm(2x7,3x15)=630
(14,15) ==> ppcm(2x14,3x15)=1260
(30,7) ==> ppcm(2x30,3x7)=420
(35,6) ==> ppcm(2x35,3x6)=630
...
...
Les calculs nous montre que le maximal 1260 est atteint par des permutations paires sig(u)=sig(v)=1 et que u et v valent
u = (7-cycle)(2-cycle)(2-cycle)(1-cycle)
v = (5-cycle)(3-cycle)
|u| = ppcm(7,2,2,1)=14
|v| = ppcm(5,3)=15
ppcm(2x14,3x15)=1260

L'ordre maximal dans G

C'est pratiquement fini, il suffit de prendre un élément de G⁺ d'ordre maximal et montrer qu'il est dans G
On prend
(u,x,v,y)∈G⁺
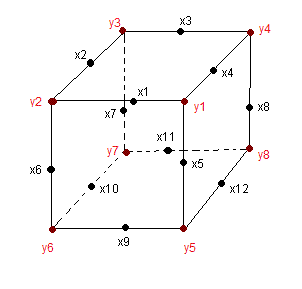
u = (1,7,12,5,2,4,3)(8,10)(9,11)(6) et x=(1,0,0,1,0,0,1,0,0,1,0,0)
v = (4,6,5,8,7)(1,2,3) et y=(2,2,0,1,2,2,1,2)
(u,x,v,y) vérifie tous les conditions pour être dans G, (u,x,v,y)∈G et son ordre 1260
NOTE: On a la formule associée DH²B'PB' , et (DH²B'PB')¹²⁶⁰ = I

Sommets et arêtes

Résumons

1. L'ordre ne dépend pas de l'orientation
2. L'ordre d vaut: d|m où m=ppcm(2|u|,3|v|) avec sig(u)=sig(v)
3. L'ordre maximal d_max donné par
   
   
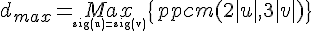
4. Le maximal est atteint pour
   u = (7-cycle)(2-cycle)(2-cycle)(1-cycle) ; permutation paire
   v = (5-cycle)(3-cycle) ; permutation paire
   Rappel la formule qui donne l'ordre 1260: DH²B'PB'
   Il est remarquable que l'ordre maximal du Rubik est un quadrix !! 1260 = [(4!+4)/4]!/4 , il suffit de remarquer
   1260 = 35.36 = 7.5.9.4 = 7.6.5.3.2 = 7!/4
   

D'après (2) l'ordre d est un diviseur de m : d|m et on trouve 73 ordres voici ces ordres avec les formules associées, les longeurs sont des plus courtes

N°: Ordre → Formule

01: 01 → I
02: 02 → H²
03: 03 → H D H' B' D B
04: 04 → H
05: 05 → H D H D'
06: 06 → [HD]=H D H' D'
07: 07 → H D H' A
08: 08 → H D² B
09: 09 → H D A²
10: 10 → H' D H A
11: 11 → (H D A² P B')² ; pas facile à trouver! longueur=12, c'est la plus longue parmi les 73 ordres
12: 12 → H D A B'
13: 14 → H' D H D' A B
14: 15 → H D² H D²
15: 16 → H D H' A B
16: 18 → H D H' D' A
17: 20 → H D H' G²
18: 21 → H² D H² A
19: 22 → H D A² P B'
20: 24 → H D² B'
21: 28 → H D H' G
22: 30 → H D²
23: 33 → H D A' B'
24: 35 → H² D H² G'
25: 36 → H² D' A'
26: 40 → H D H² G
27: 42 → H D² H² D'
28: 44 → H' D A' B
29: 45 → H D H G
30: 48 → H² D H A
31: 55 → H D A' H' B' G
32: 56 → H² D A' B
33: 60 → H D' A'
34: 63 → H D'
35: 66 → H D H A² G'
36: 70 → H D H' D A B'
37: 72 → H D H A'
38: 77 → H D' A' G'
39: 80 → H' D' A'
40: 84 → H D A
41: 90 → H D B
42: 99 → H D² A G²
43: 105 → H D
44: 110 → D' H D A B' B' G'
45: 112 → H D' H A' D B
46: 120 → H D A G'
47: 126 → H' D A' G'
48: 132 → H D A' G
49: 140 → H D' H A'
50: 144 → H D' A' B²
51: 154 → H D H A G B'
52: 165 → H D' H A² G'
53: 168 → H D B²
54: 180 → H D B'
55: 198 → H² D A B²
56: 210 → H D' B G'
57: 231 → H D A' B
58: 240 → H' D A' G²
59: 252 → H D A G
60: 280 → H' D' H' A G'
61: 315 → H D B G
62: 330 → H² D A' B' G'
63: 336 → H D H A B²
64: 360 → H D A'
65: 420 → H D B G'
66: 462 → H' D A' B² G'
67: 495 → H D² H A' G'
68: 504 → H D² A G'
69: 630 → H' D' H' A' G²
70: 720 → H' D' H' A' B²
71: 840 → H² D' A' B
72: 990 → H' D' H' A' G B
73: 1260 → H D' H A' B²

1 [2]

Accueil

DMJ: 09/03/2022