Le Megaminx

1- Notation

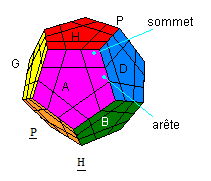
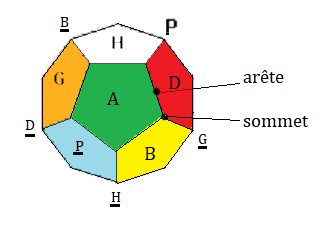
Prenez votre Mégaminx et posez le sur la table, comme ceci:.


Les noms des faces... :
H(aut) , B(as), H(aut-opposé) | A(vant) , P(ostérieur) | G(auche) , D(roite), D(roite-opposé)...

Les rotations
A = tourner 72° la face Avant dans le sens positif (sens des aiguilles d'une montre).
A' = tourner -72° (dans le sens négatif)
A² = tourner 2x72°=144° dans le sens positif

On écit (HA) pour désigner le arête Haut-Avant ou (HAD) le sommet Haut-Droire-Avant
(HA)° = pivoter le arête (HA)
(HDA)° = pivoter le sommet (HDA)
Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!

Les 3 lois du Megaminx

Le Megaminxe possède 3 lois, comme le Rubik's Cube: une sur les permutations et deux sur l'orientation. Voyons un peu

Loi de parité:
les permutations des arêtes et des sommets ont la signature = 1

si u est la permutation des arêtes et v la permutation des sommets alors
sig(u) = sig(v) = 1.

Une rotation de base A, par exemple, fait permuter 5 arêtes et 5 sommets, un 5-cycle pour les arêtes, et un 5-cycle pour les sommets
Soient p = permutation des arêtes et q = permutation des sommets

donc sig(p)=sig(q)=1

Démontrons cette loi par récurrence
Au départ (n=0) on a u=id (id=identité) et v=id car on ne fait rien, on a bien sig(u)=sig(v)=1
Supposons donc un mouvement T de longueur n avec l = permutation des arêtes et m = permutation des sommets , et sig(l) = sig(m) = 1
et soit S un mouvement de longueur n+1, avec u = permutation des arêtes et v = permutation des sommets , on passe de T à S par une rotation de base Z
S = TZ
sig(u)=sig(l).sig(p)=1x1=1
sig(v)=sig(m).sig(q)=1x1=1
d'où
sig(u)=sig(v)=1
La 1ère loi est ainsi démontrée.

Orientation des arêtes

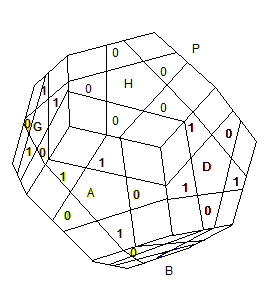
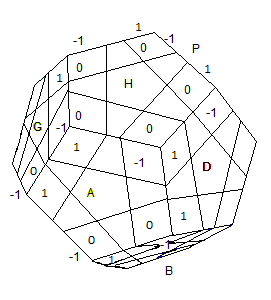
On a des emplacements-arêtes à 2 facettes marquées comme l'indique la fig.1 ci-dessous

Voici le marquage
1. La face H que des 0
2. 1er couronne: (AD) avec A=0, (DP) avec D=0, (PB) avec P=0, etc ...
3. 2eme couronne: (AB) avec A=1 , (AP) avec A=0, (DG) avec D=1, (DB) avec D=0, etc ...
4. 3eme couronne (comme 1er couronne , retournez le cube): (BP) avec B=0 , (BD) avec P=0 , ...
5. La face h que des 0

fig1: emplacements-arêtes avec les facettes marquées 0 = bien orienté

H ==> 0 = 0 (mod 2)
A ==> 1+1+1+1 =0 (mod 2)
B ==> 1+1 = 0 (mod 2)

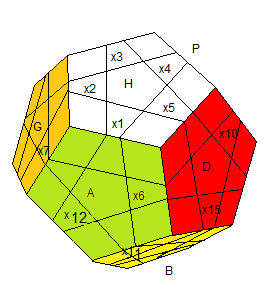
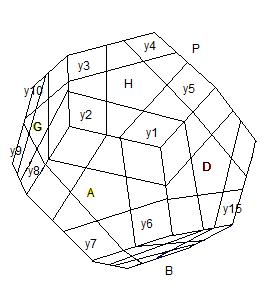
Les arêtes ayant 2 couleurs (numérotées comme l'indique le fig.2 ) dont l'une est dominante.

fig2: Les arêtes numérotées Les xi sur 0

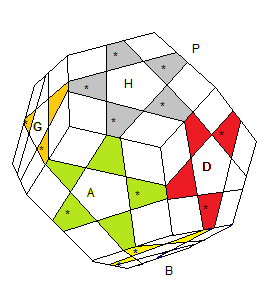
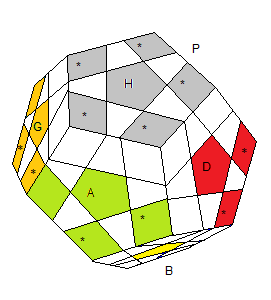
Voici les arêtes avec leur couleur dominante (couleur marquée *) en premier:

x₁=(bv), x₂=(bo), x₅=(br), ...
x₆=(vr), ...

* = les couleurs dominantes

Les arêtes x_i se baladent pour se loger dans des emplacements-arêtes, à chaque fois que la couleur dominante se trouve sur une facette marquée 1 sa orientation vaut 1 (1 flip), sinon elle vaut zéro (0=bien orienté), Par exemple l'arête (vr) = x₆ se place en (HA) avec vert=H, alors x₆ vaut 0 (0 flip, bien orienté) car la couleur dominante vert est sur la facette marquée 0, De même, si l'arête (bk) = x₄ est dans (AD)=x₄ avec blanc=D alors x₄ = 1 (1 flip) car la couleur dominante blanc se trouve sur 1

Loi des flips: la somme des orientations des arêtes est un multiple de 2 (un nombre pair)

∑ x_i = 0 (mod 2) ou en abrégé x = 0 (mod 2) avec x = (x₁,x₂,x₃,...,x₃₀)
on dit qu'il y a une conservation des flips .

Les mouvements du Megaminx se composent à partir des rotations de base M = < H, B, A, P, G, D, h, b, a, p, g, d > il suffit donc de voir ce qui se passe pour les rotations de base, voyons par exemple pour A
D'après le marquage on a:
(HA)=(x₁,1+x₁), (AD)=(x₆,1+x₆), (BA)=(x₁₆,1+x₁₆), (PA)=(x₁₁,1+x₁₁), (AG)=(x₇,1+x₇)
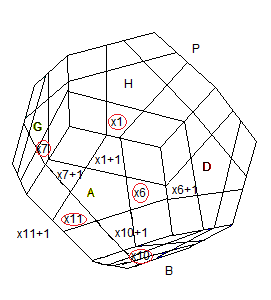
Remarque : Les x_i sont placés sur le marquage 0

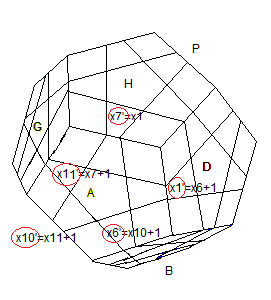Avant rotation A	Après rotation A

Permutation: p = 1->6->10->11->7 = (1,6,10,11,7)

x'₁ = 1+x₆
x'₆ = 1+x₁₀
x'₇ = x₁
x'₁₀ = 1+x₁₁
x'₁₁ = 1+x₇

x'= a + p(x)

On note 0xn pour dire qu'il y a n zéro exp: (...,1,0x5,1,...)=(...,1,0,0,0,0,0,1,...)
Orientation: a = (1,0x4,1,1,0,0,1,1,0x19) on a bien a = 0 (mod 2)

Démonstration :
On va démontrer par récurrence:
Supposons à l'étape n (T formule de longueur n, état (u,x)) l'orientation des arêtes vaut x = 0 (mod 2).
On passe de l'étape n à l'étape n+1 (T' formule de longueur n+1, état (u',x') ) par une rotation de base par ex A, e•A=(p,a).
T' = TA ==> (u',x') = (u,x)(p,a)
Donc
x' = x + u(a)
comme x=0 (mod 2) l'hypothèse de récurrence
et a = 0 (mod 2) et que la permutation u ne change rien sur le modulo , on a
x' = 0 (mod 2).

à l'étape (n+1) les arêtes ont une orientation un multiple de 2, comme au départ, à l'état résolu l'orientation des arêtes vaut 0, donc quelque soit l'état du cube l'orientation des arêtes est toujours un multiple de 2. On a fait la démontration pour la rotation A et on ferra la même chose pour les autres rotation de base.

la 2ème loi est ainsi démontrée.

Orientation des sommets

Ici on fait la même chose comme pour les arêtes, il y a des emplacements-sommets à 3 facettes marquées comme indiqué sur la fig.5, et les sommets (numérotés comme indiqué la fig.6 ) ayant 3 couleurs dont l'une est dominante.

Voici le marquage
1. La face H que des 0, puis dans le sens horaire on marque 1,-1
2. La face Avant: pour les sommets (ADB),(ABP) on marque A=0 puis dans le sens horaire on marque 1,-1
3. Tourner le cube ^tH: marquer D, comme la face A
4. Retourner le cube on marquee H comme H

fig5: emplacements-sommets avec les facettes marquées 0 = bien orienté

	fig6: Les sommets numérotés

Voici les sommets avec la couleur dominante en premier:
y₁=(brv), y₂=(bvo), y₅=(bkr), ...
y₆=(vrj), ...

* = les couleurs dominantes

Les sommets y_i se baladent pour se placer dans les emplacements-sommets, à chaque fois que la couleur dominante se trouve sur une facette marquée 1 son orientation vaut 1 (1 twist) , sur -1 son orientation vaut -1 (-1 twist) , sur 0 son orientation vaut zéro (0 twist, 0=bien orienté). Par exemple, le sommet (vrj) = y₆ se place en (HDA) avec vert=A alors y₆ vaut -1 (-1 twist) car la couleur dominante vert est sur la facette -1, de même pour le sommet (bvo) = y₂ dans (HAG) avec blanc=A alors y₂ = 1 (1 twist) car la couleur dominante blanc se trouve sur 1 .

Loi des twists :
la somme des orientations des sommets est un multiple de 3

∑ y_i = 0 (mod 3) ou en abrégé y = 0 (mod 3) avec y = (y₁,y₂,y₃,...,y₂₀)
on dit qu'il y a une conservation des twists .

Il suffit de montrer que c'est vrai pour une rotation de base par exemple A, e•A=(q,b).
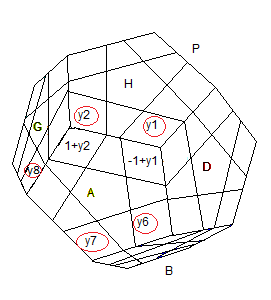
D'après le marquage on a:
(HDA)=(y₁,1+y₁,-1+y₁), (ADB)=(y₆,1+y₆,-1+y₆),
(ABP)=(y₇,1+y₇,-1+y₇), (APG)=(y₈,1+y₈,-1+y₈)
(HAG)=(y₂,1+y₂,-1+y₂)
Remarque : Les y_i sont placés sur le marquage 0

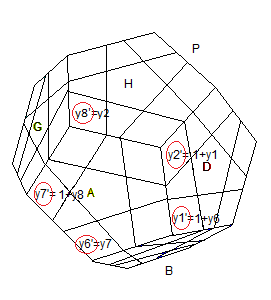
Avant la rotation A	Après la rotation A

Permutation: q = 1->6->7->8->2 = (1,6,7,8,2)

y'₁ = 1+y₆
y'₂ = 1+y₁
y'₆ = y₇
y'₇ = 1+y₈
y'₈ = y₂

y' = b + q(y)
Orientation: b = (2,2,0x5,2,0x12) on a bien b = 0 (mod 3)

Démonstration :
On va démontrer par récurrence:
Supposons à l'étape n (T formule de longueur n, état (v,y) ) l'orientation des sommets vaut y = 0 (mod 3).
On passe de l'étape n à l'étape n+1 (T' formule de longueur n+1, état (v',y') ) par une rotation de base par ex A, e•A=(q,b).
T' = TA ==> (v',y') = (v,y)(q,b)
Donc
y' = y + v(b)
comme y = 0 (mod 3) l'hypothèse de récurrence
et b = 0 (mod 3) et que la permutation v ne change rien sur le modulo , on a
y' = 0 (mod 3).
Donc à l'état (n+1) les sommets ont une orientation un multiple de 3, comme au départ, à l'état resolu l'orientation des sommets vaut 0, donc quelque soit l'état du cube l'orientation des sommets est toujours un multiple de 3. On a fait la démontration pour la rotation A et on ferra la même chose pour les autres rotation de base.

la 3ème loi est ainsi démontrée.

[1] 2

Accueil

DMJ: 02/05/2024