Le groupe G du Megaminx

1- Notation

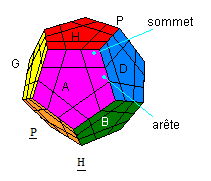
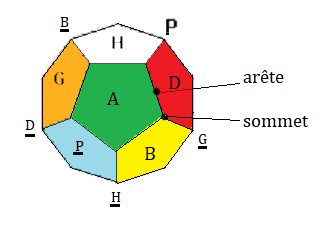
Prenez votre Mégaminx et posez le sur la table, comme ceci:.


Les noms des faces... :
H(aut) , B(as), H(aut-opposé) | A(vant) , P(ostérieur) | G(auche) , D(roite), D(roite-opposé)...

Les rotations
A = tourner 72° la face Avant dans le sens positif (sens des aiguilles d'une montre).
A' = tourner -72° (dans le sens négatif)
A² = tourner 2x72°=144° dans le sens positif

On écit (HA) pour désigner le arête Haut-Avant ou (HAD) le sommet Haut-Droire-Avant
(HA)° = pivoter le arête (HA)
(HDA)° = pivoter le sommet (HDA)
Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!

Construction le groupe G du Megaminx

(i) - On a 30 arêtes qui baladent partout dans leur camp, donc on a affaire avec S₃₀, mais les arêtes peuvent aussi se pivoter en 2 positions c'est un truc Z₂³⁰, pour les arêtes tout se passe dans:
S₃₀ x Z₂³⁰
- De même on a 20 sommets qui baladent partout dans leur camp, donc on a affaire avec S₂₀, mais les sommets peuvent aussi se pivoter en 3 positions c'est un truc Z₃²⁰, pour les sommets tout se passe dans:
S₂₀ x Z₃²⁰

On pose :
G⁺ = S₃₀ x Z₂³⁰ x S₂₀ x Z₃²⁰ c'est l'ensemble des configurations.
G⁺ muni la loi suivante, qui lui confère un groupe .
(u,x,v,y)(u',x',v',y') = ( uu', x+u(x'), vv', y+v(y') )
uu' = u' o u
u(x) = (x_u(1), x_u(2), ..., x_u(n)) ; u=permutation , x=vecteur

(ii) Soient M = < H, B, A, P, G, D, H, B, A, P, G, D, > l'ensemble des formules engendrées par les 12 rotations de base,
(M,.) : '.' loi concaténation

(iii) Action '•' de M sur G⁺ :
G⁺ x M --> G⁺
(s,V) --> s•V=t∈G⁺
A₁ : s•I = s ;élément neutre
A₂ : (s•V)•T = s•(VT) ;associativité
A₃ : a∈G⁺ donné, fixé
a•V = a ==> V = I ;librement
librement ==> I est la seule formule ayant des points fixes.
A₄ : s•(VT) = (s•V)(s•T) ;compatibilité

(iv) Définition de G : G = {s∈G⁺ / e•V = s , V∈M} , e=état résolu
Les éléments de G se nomment état

(v) théorème fondamental :
s=(u,x,v,y)∈G⁺
u ∈S₃₀, x ∈Z₂³⁰, v ∈S₂₀, y ∈Z₃²⁰
on pose:
(F) ∑ x_i = 0 (mod 2) en abrégeant x=0 (mod 2) avec x = (x₁,x₂,...,x₃₀)
(T) ∑ y_i = 0 (mod 3) en abrégeant y=0 (mod 3) avec y = (y₁,y₂,...,y₂₀)
(P) sig(u) = 1
(Q) sig(v) = 1

D'apès les lois le nombre de contraintes N est donc:
N = 2.3.2.2

théorème : G = {s∈G⁺ / s vérifie (F), (T), (P), (Q)}

Démonstration du théorème fondamental

Quelles sont les conditions nécessaires et suffisantes pour qu'une configuration soit un état ?

Condition suffisante

On prend donc un élément s de G , et il faut trouver une formule dont il provient
La démontration est constructive, on construit la formule petit à petit
s=(u,x,v,y)∈G⁺ vérifiant les trois conditions (F), (T), (P) et (Q)
On va faire ça en plusieurs étapes.
On coupe (u,x,v,y) en plusieurs morceaux

Cas les arêtes: (u,x)=(u,x,id,0)
Soient les 2 formules suivantes:
F₁ = G[HA]G' => pivote 2 arêtes
F₂ = DHD'. H . DH³D' => glisse 3 arêtes sans perturber l'orientation des arêtes, un 3-cycle
On coupe l'état-arête (u,x) = (id,x)(u,0)

-On utilise F₁ (et la conjugaison) , pour pivoter les arêtes une par une comme exige x, la dernière sera automatiquement correcte à cause de x=0 (mod 2)

-On utilise F₂ (et la conjugaison), pour glisser toutes les arêtes à leur place comme exige u, c'est possible car F₂ est un 3-cycle , et que les 3-cycle engendre A₃₀ (on est dans A₃₀ car sig(u)=1)

Cas les sommets: (v,y)=(id,0,v,y)
Soient les 2 formules suivantes:
F₃ = [HA] .P'[AH]P => placer 3 sommets, un 3-cycle
F₄ = [HA]² .P'[AH]² P => pivoter 2 sommets

On va couper l'état-sommet (v,y) en plusieurs morceaux, c'est un peu plus compliqué que pour les arêtes.
Voyons:
D'après les formule F₃ et F₄ ceci nous suggère de couper (v,y) ainsi:
(v,z)(id,y) = (v,y)
ce qui donne:
z = y - v(y)
Finalement on coupe
(v,y) = (v,y-v(y))(id,y)

Bref : On place des sommets, si l'orientation change on les pivote avec F₄

-On utilise F₃ (et la conjugaison), pour placer toutes les sommets comme exige v, c'est possible car F₃ est un 3-cycle , et que les 3-cycle engendre A₂₀ (on est dans A₂₀ car sig(v)=1)

-On utilise F₄ (et la conjugaison) , pour pivoter les sommets comme exige y-v(y), le dernier sera automatiquement bien pivoté à cause de y=0 (mod 3)

-On utilise de nouveau F₄ (et la conjugaison) , pour pivoter les sommets comme exige y, le dernier sera automatiquement bien pivoté à cause de y=0 (mod 3)

Finalement pour trouver une formule pour l'état (u,x,v,y) on fait simplement :
- Utiliser les formules F₁,F₂ pour ranger les arêtes ==> (u,x, . , . )
- Utiliser la formule F₃,F₄ pour ranger les sommets ==> (.,.,v,y)
Donc l'état (u,x,v,y) correspond bien à une formule

Condition nécessaire

On prend donc une formule V -un élément de M- , la formule gènère un état e•V=(u,x,v,y)∈G⁺, il faut montrer que
(F) x=0 (mod 2)
(T) y=0 (mod 3)
(P) sig(u) = 1
(Q) sig(v) = 1

(P)+(Q) ==> Pour une rotation de base, on a sig(p)=sig(q)=1 donc pour une formule on a:
sig(u) = sig(p) x sig(p') x sig(p")... = 1x1x1 ... = 1 et
sig(v) = sig(q) x sig(q') x sig(q")... = 1x1x1 ... = 1

(F)+(T) ==> On va raisonner par récurrence sur n=|V|, longueur de la formule V
Pour n=1 , on a x=0 (mod 2) et y=0 (mod 3) pour toute rotation de base
Supposons que la propriété soit vraie pour n (formule V, état e•V=(u,x,v,y)), montrons qu'elle reste encore vraie pour n+1 (formule Q, état e•Q=(u',x',v',y'))
mais on passe de n à n+1 par une rotation de base Z, e•Z=(p,a,q,b)
V' = VZ
e•V' = e•(VZ) = (e•V)(e•Z) ; Axiome4
(u',x',v',y') = (u,x,v,y)(p,a,q,b) = (up,x+u(a),vq,y+v(b))
x' = x + u(a)
y' = y + v(b)
comme
x=0 (mod 2) l'hypothèse de récurrence
a=0 (mod 2) ; vrai pour toute rotation de base
u(a)=0 (mod 2) une permutation ne change pas le modulo de a
d'où
x'=0 (mod 2)

de même
y=0 (mod 3) l'hypothèse de récurrence
b=0 (mod 3) ; vrai pour toute rotation de base
v(b)=0 (mod 3)
d'où
y'=0 (mod 3)

G⁺ = S₃₀ x Z₂³⁰ x S₂₀ x Z₃²⁰
G = G⁺/N = S₃₀ x Z₂³⁰ x S₂₀ x Z₃²⁰ / N
|G| = |G⁺|/N = 30! .2³⁰ ..20! .3²⁰ / 2.3.2.2 = 30! .2²⁷ .20! .3¹⁹

Résumer: Toute formule produit un élément de G, tout élément de G provient de M
Remarque :
Bien que M et G sont isomorphes mais on ne peut pas identifier G=M, en effet, M agit sur G et non le contraire !!!

1 [2]

Accueil

DMJ: 03/11/2024