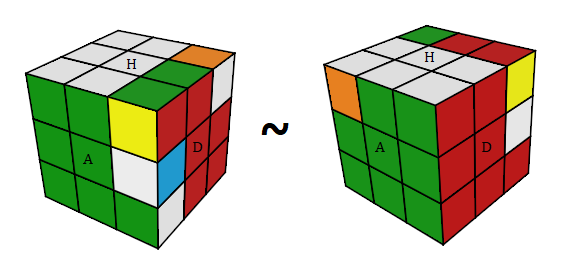La symétrie J-conjugaison

Au début ...

Il faut remonter vers les années 1980 , on s'est posé la question suivante:
-Quel est le nombre de rotations nécessaire b, pour restaurer le Rubik's Cube à partir de n'importe quel état ?
On peut prendre par ex b = 65256 c'est bien, mais il y a beaucoup trop de rotations non utilisées ....
de même si on prend b = 23 , il y a des états qu'on ne peut pas s'en sortir avec 23 rotations par ex l'état SuperFlip !!
Chercher b revienr à chercher le diamètre du Rubik's Cube.

Donc on a le graphe (le graphe Cayley) du Rubik's Cube mais ce graphe est énorme !!! l'idée est de réduire ce graphe à fin que la recherche du diamètre soit accessible par l'ordinateur ...
En 1994 Dan HOEY a eu l'idée suivante : On va classer les états suivant un certain nombre de critères, ainsi on réduit le nombre de sommets donc on réduit le graphe. Mais alors quels sont les critères ? les critères utilisés connus sous le nom de: "La symétrie J-conjugaison" !!

Avant de parler "mathématiquement" du Rubik's Cube il faut "orienter" le Cube càd déclarer officielement qui est le Haut, qui est la Droite ....
traditionnellement on oriente le Cube ainsi:

H(aut)=b(lanc), B(as)=j(aune), A(vant)=v(ert), P(ostérieur)=k(lein), G(auche)=o(range), D(roite)=r(ouge).

La symétrie J

On commence par la "symétrie J". Observons ces trois images ci-dessous
Parmi ces trois images lequel est l'état résolu ? et pourquoi ?

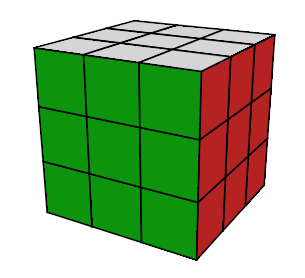image (a)	image (b)

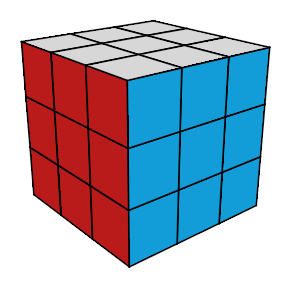image (c)

L'image (b) est l'état résolu car les centres ne sont pas bougés, comme les centres de (a) et de (c) ont bougé ces images ne présentent pas l'état résolu ! et pourtant si on tient un Rubik's Cube résolu à la main ces 3 états jouent le même rôle .... d'où l'idée de classer (mettre dans la même boîte) les états du Rubik's Cube (en ignorant les centres) suivante un certain nombre de critères .... à fin que les états (a), (b), (c) soient dans la même classe, dans la même boîte.

Le critère utilisé est la "symétrie J" où J est le groupe des isométries du cube, il a 48 éléments en voici :

Isométries positives
===================
Identité (1)
RotCentre±90° (3+3)
RotCentre180° (3)
RotArete180° (6)
RotSommet±120° (4+4)

Isométries négatives
====================
SymCentrale (1)
SymRot±90° (3+3)
SymPlan (3)
SymArete (6)
SymSommet (4+4)
----------------------
Total = 48 éléments

J agit (ligrement) sur G (on ignore les centres):
G x J ---> G
(s,f) ---> s•f

on définit la symétrie J ainsi:

Deux états s, t sont dans la même classe (même boîte) ssi:
il existe un f€J tel que s•f = t
ex
b•(^tA^tD') = a
b•(^tH) = c

Formule de Burnside

Rappelle sur la formule de Burnside.
Soient K un groupe fini et X un ensemble fini, K agit sur X (on passe un élément de X à un autre par un élément de K)
On pose F_g = { x ∈X / x•g = x } l'ensemble des points fixes de g∈K , F_g ⊂ X

Lemme de Burnside
N = 1/|K| . ∑_g∈K |F_g|
où N = le nombre d'orbites
C'est la somme des points fixes quand g parcourt K

On prend K=J et X=G
N = |G| / 48 = 901 083 401 551 872 000 J-classes

La symétrie J-conjugaison

On veut que 2 états ci-dessous soient équivalences

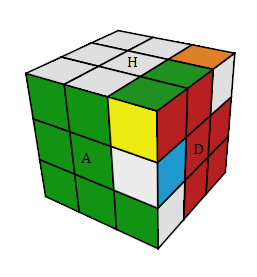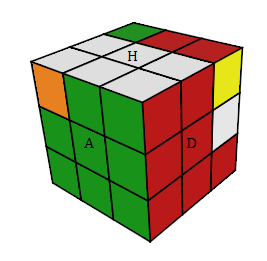image (a)	image (b)

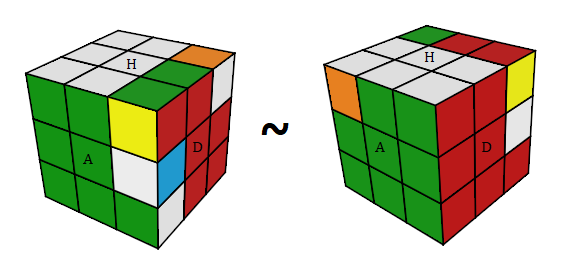image (c)

Si on tient le Cube dans la main ces 2 états jouent le même rôle .... d'où l'idée de classer (mettre dans la même boîte) les états du Rubik's Cube suivante un certain nombre de critères .... à fin que les états (a), (b) soient dans la même classe, dans la même boîte.

Le critère utilisé est la "symétrie J-conjugaison" où J est le groupe des isométries du cube,

J agit (librement) sur G :
G x J ---> G
(s,f) ---> e•(fVf^-1) ,où s=e•V

NOTE : f perturbe les centres, V ne touche pas les centres, f^-1 remet en ordre les centres, J agit bien sur G.

on définit la symétrie J-conjugaison ainsi:

Deux états s=e•V et t sont dans la même classe (même boîte) ssi:
il existe un f€J tel que e•(fVf^-1) = t ,
ex
s = e•V , V=DHD'H'
e•(^tH V ^tH') = t

Avec un programme informatique on a trouvé 901 083 404 981 813 616 J-conjugaison classes .

Les classes se distribuent en fonction des éléments de J de la façon suivante:

Classe de Type . . . . . Nombre de classes
============== . . . . . =================
Identité (1) = 901 083 401 551 872 000

RotCentre±90° (3+3) = 18 432

RotCentre180° (3) = 955 514 880

RotArete180° (6) = 318 504 960

RotSommet±120° (4+4) = 629 856

------------------

SymCentrale (1) = 955 514 880

SymRot±90° (3+3) = 55 296

SymPlan (3) = 1 146 617 856

SymArete (6) = 53 084 160

SymSommet (4+4) = 1 296

------------- . . . . . -----------------------
48 éléments , Total = 901 083 404 981 813 616

Chaque classe contient donc un certain nombre d'états.

Le nombre 901 083 404 981 813 616 est donc le nombre de J-conjugaison classes et non le nombre d'états de G !!.

Les programmes en GAP

Voici 3 programmes en GAP qui permettent de calculer le nombre de J-conjugaison classes du Rubik's Cube ou du Pocket

Programme 1

# 5 6 7
# 4 H 8
# 3 2 1
#25 28 23|21 26 19|17 32 31|29 30 27
#38 G 36|12 A 10|34 D 40|16 P 14
#43 44 37|39 42 33|35 48 45|47 46 41
# 11 18 9
# 20 B 24
# 13 22 15

# Iso=le groupe isometrie du cube
j1 := (6,46,18,26)(8,14,24,12)(38,48,36,32)(2,30,22,42)(16,20,10,4)(28,40,44,34)
(5,45,11,17)(7,13,9,3)(21,31,41,35)(43,33,23,29)(1,25,15,37)(47,39,19,27) ;
j2 := (6,16,22,14)(8,24,20,4)(38,30,40,46)(2,10,18,12)(28,32,48,44)(34,42,36,26)
(5,31,15,43)(7,45,13,25)(21,19,33,39)(1,35,11,23)(47,41,27,29)(3,17,9,37);
Iso := Group(j1,j2) ;

# Dep=le groupe isometrie+ du cube (24) Dep = ssg de Iso
Dep := Group( (1,11)(2,18)(3,9)(4,24)(5,15)(6,22)(7,13)(8,20)(10,12)
(14,16)(17,37)(19,39)(21,33)(23,35)(25,45)(26,42)(27,47)(28,48)(29,41)
(30,46)(31,43)(32,44)(34,36)(38,40),
(1,15)(2,22)(3,13)(4,20)(5,11)(6,18)(7,9)(8,24)(10,16)(12,14)
(17,45)(19,47)(21,41)(23,43)(25,37)(26,46)(27,39)(28,44)(29,33)(30,42)
(31,35)(32,48)(34,40)(36,38),
(1,17,19)(2,32,10)(3,31,33)(4,40,42)
(5,45,39)(6,48,12)(7,35,21)(8,34,26)(9,23,29)(11,25,47)(13,43,41)
(14,22,44)(15,37,27)(16,18,28)(20,38,46)(24,36,30),
(1,35,11,23)(2,10,18,12)(3,17,9,37)(4,8,24,20)(5,31,15,43)
(6,16,22,14)(7,45,13,25)(19,33,39,21)(26,34,42,36)(27,29,47,41)
(28,32,48,44)(30,40,46,38) ) ;

# Rubik=le groupe du Rubik's Cube
pH := (2,4,6,8)(26,28,30,32) (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
pB := (18,24,22,20)(42,48,46,44) (9,15,13,11)(33,45,41,37)(35,47,43,39);
pA := (2,34,18,36)(26,10,42,12) (1,35,11,23)(17,9,37,3)(19,33,39,21);
pP := (6,38,22,40)(30,14,46,16) (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
pG := (4,12,20,14)(28,36,44,38) (3,39,13,27)(21,11,41,5)(23,37,43,25);
pD := (8,16,24,10)(32,40,48,34) (1,29,15,33)(17,31,45,35)(19,7,47,9);
Rubik := Group(pH,pB,pA,pP,pG,pD);

# Pocket=le groupe Pocket (= Rubik sans arêtes)
#pH := (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
#pB := (9,15,13,11)(33,45,41,37)(35,47,43,39);
#pA := (1,35,11,23)(17,9,37,3)(19,33,39,21);
#pP := (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
#pG := (3,39,13,27)(21,11,41,5)(23,37,43,25);
#pD := (1,29,15,33)(17,31,45,35)(19,7,47,9);
#Pocket := Group(pH,pB,pA,pP,pG,pD);

G := Rubik ;;
GG := "Rubik" ;;
J := Iso ;;
JJ := "J" ;;

etat := 0 ;;
Jcjg := 0 ;;

# Les classes des sous groupes conjugaisons de J
Cl := ConjugacyClassesSubgroups( J );;
ptfixe := [];

Print("\n\n No \tetat \tclasses-conjugaisons\n" );
Print("================================================== \n" );
# pour tout classe Cl[i], on cherche les pt fixes générés par Cl[i]
for i in [Length(Cl),Length(Cl)-1..1] do

# prendre un représentant
H := Representative( Cl[i] );

# les pt fixes engendrés par H
aux := Size( Centralizer( G, H ) );

# si Q inclus dans H,on supprime dans H les pt fixes générés par Q
for k in [Length(Cl),Length(Cl)-1..i+1] do
for Q in Elements( Cl[k] ) do
if IsSubgroup( Q, H ) then
aux := aux - ptfixe[k];
fi;
od;
od;

# sauver les pt fixes génégrés par H
ptfixe[i] := aux;

# print N° classe
Print("\n ", i, ":\t" );

# le nbr de pt fixes (= nbr états) générés par Cl[i]
Print( Size(Cl[i]) * ptfixe[i], "\t" );
etat := etat + ( Size(Cl[i]) * ptfixe[i] );

# le nbr de J-cjg classes générés par Cl[i]
Print( (Size(Cl[i]) * ptfixe[i]) / Index(J,H), " " );
Jcjg := Jcjg + ( (Size(Cl[i]) * ptfixe[i] )/ Index(J,H) );

od;
Print("\n\n ",GG," = ", etat, "\n" );
Print("\n ",JJ,"-cjg = ", Jcjg , "\n" );

Programme 2

# 5 6 7
# 4 H 8
# 3 2 1
#25 28 23|21 26 19|17 32 31|29 30 27
#38 G 36|12 A 10|34 D 40|16 P 14
#43 44 37|39 42 33|35 48 45|47 46 41
# 11 18 9
# 20 B 24
# 13 22 15

# Iso=le groupe isometrie du cube
j1 := (6,46,18,26)(8,14,24,12)(38,48,36,32)(2,30,22,42)(16,20,10,4)(28,40,44,34)
(5,45,11,17)(7,13,9,3)(21,31,41,35)(43,33,23,29)(1,25,15,37)(47,39,19,27) ;
j2 := (6,16,22,14)(8,24,20,4)(38,30,40,46)(2,10,18,12)(28,32,48,44)(34,42,36,26)
(5,31,15,43)(7,45,13,25)(21,19,33,39)(1,35,11,23)(47,41,27,29)(3,17,9,37);
Iso := Group(j1,j2) ;

# Dep=le groupe isometrie+ du cube (24) Dep = ssg de Iso
Dep := Group( (1,11)(2,18)(3,9)(4,24)(5,15)(6,22)(7,13)(8,20)(10,12)
(14,16)(17,37)(19,39)(21,33)(23,35)(25,45)(26,42)(27,47)(28,48)(29,41)
(30,46)(31,43)(32,44)(34,36)(38,40),
(1,15)(2,22)(3,13)(4,20)(5,11)(6,18)(7,9)(8,24)(10,16)(12,14)
(17,45)(19,47)(21,41)(23,43)(25,37)(26,46)(27,39)(28,44)(29,33)(30,42)
(31,35)(32,48)(34,40)(36,38),
(1,17,19)(2,32,10)(3,31,33)(4,40,42)
(5,45,39)(6,48,12)(7,35,21)(8,34,26)(9,23,29)(11,25,47)(13,43,41)
(14,22,44)(15,37,27)(16,18,28)(20,38,46)(24,36,30),
(1,35,11,23)(2,10,18,12)(3,17,9,37)(4,8,24,20)(5,31,15,43)
(6,16,22,14)(7,45,13,25)(19,33,39,21)(26,34,42,36)(27,29,47,41)
(28,32,48,44)(30,40,46,38) ) ;

# Rubik=le groupe du Rubik's Cube
pH := (2,4,6,8)(26,28,30,32) (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
pB := (18,24,22,20)(42,48,46,44) (9,15,13,11)(33,45,41,37)(35,47,43,39);
pA := (2,34,18,36)(26,10,42,12) (1,35,11,23)(17,9,37,3)(19,33,39,21);
pP := (6,38,22,40)(30,14,46,16) (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
pG := (4,12,20,14)(28,36,44,38) (3,39,13,27)(21,11,41,5)(23,37,43,25);
pD := (8,16,24,10)(32,40,48,34) (1,29,15,33)(17,31,45,35)(19,7,47,9);
Rubik := Group(pH,pB,pA,pP,pG,pD);

# Pocket=le groupe Pocket (= Rubik sans arêtes)
#pH := (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
#pB := (9,15,13,11)(33,45,41,37)(35,47,43,39);
#pA := (1,35,11,23)(17,9,37,3)(19,33,39,21);
#pP := (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
#pG := (3,39,13,27)(21,11,41,5)(23,37,43,25);
#pD := (1,29,15,33)(17,31,45,35)(19,7,47,9);
#Pocket := Group(pH,pB,pA,pP,pG,pD);

G := Rubik ;;
GG := "Rubik" ;;
J := Iso ;;
JJ := "J" ;;

Jcjg := Sum(ConjugacyClasses(J),i -> (Size(i) * Size(Centralizer(G,Representative(i)))) / Size(J));;
Print("\n\n ",GG," = ", Size(G), "\n" );
Print("\n ",JJ,"-cjg = ", Jcjg, "\n" );

Programme 3

# 5 6 7
# 4 H 8
# 3 2 1
#25 28 23|21 26 19|17 32 31|29 30 27
#38 G 36|12 A 10|34 D 40|16 P 14
#43 44 37|39 42 33|35 48 45|47 46 41
# 11 18 9
# 20 B 24
# 13 22 15

# Iso=le groupe isometrie du cube
j1 := (6,46,18,26)(8,14,24,12)(38,48,36,32)(2,30,22,42)(16,20,10,4)(28,40,44,34)
(5,45,11,17)(7,13,9,3)(21,31,41,35)(43,33,23,29)(1,25,15,37)(47,39,19,27) ;
j2 := (6,16,22,14)(8,24,20,4)(38,30,40,46)(2,10,18,12)(28,32,48,44)(34,42,36,26)
(5,31,15,43)(7,45,13,25)(21,19,33,39)(1,35,11,23)(47,41,27,29)(3,17,9,37);
Iso := Group(j1,j2) ;

# Dep=le groupe isometrie+ du cube (24) Dep = ssg de Iso
Dep := Group( (1,11)(2,18)(3,9)(4,24)(5,15)(6,22)(7,13)(8,20)(10,12)
(14,16)(17,37)(19,39)(21,33)(23,35)(25,45)(26,42)(27,47)(28,48)(29,41)
(30,46)(31,43)(32,44)(34,36)(38,40),
(1,15)(2,22)(3,13)(4,20)(5,11)(6,18)(7,9)(8,24)(10,16)(12,14)
(17,45)(19,47)(21,41)(23,43)(25,37)(26,46)(27,39)(28,44)(29,33)(30,42)
(31,35)(32,48)(34,40)(36,38),
(1,17,19)(2,32,10)(3,31,33)(4,40,42)
(5,45,39)(6,48,12)(7,35,21)(8,34,26)(9,23,29)(11,25,47)(13,43,41)
(14,22,44)(15,37,27)(16,18,28)(20,38,46)(24,36,30),
(1,35,11,23)(2,10,18,12)(3,17,9,37)(4,8,24,20)(5,31,15,43)
(6,16,22,14)(7,45,13,25)(19,33,39,21)(26,34,42,36)(27,29,47,41)
(28,32,48,44)(30,40,46,38) ) ;

# Rubik=le groupe du Rubik's Cube
pH := (2,4,6,8)(26,28,30,32) (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
pB := (18,24,22,20)(42,48,46,44) (9,15,13,11)(33,45,41,37)(35,47,43,39);
pA := (2,34,18,36)(26,10,42,12) (1,35,11,23)(17,9,37,3)(19,33,39,21);
pP := (6,38,22,40)(30,14,46,16) (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
pG := (4,12,20,14)(28,36,44,38) (3,39,13,27)(21,11,41,5)(23,37,43,25);
pD := (8,16,24,10)(32,40,48,34) (1,29,15,33)(17,31,45,35)(19,7,47,9);
Rubik := Group(pH,pB,pA,pP,pG,pD);

# Pocket=le groupe Pocket (= Rubik sans arêtes)
#pH := (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
#pB := (9,15,13,11)(33,45,41,37)(35,47,43,39);
#pA := (1,35,11,23)(17,9,37,3)(19,33,39,21);
#pP := (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
#pG := (3,39,13,27)(21,11,41,5)(23,37,43,25);
#pD := (1,29,15,33)(17,31,45,35)(19,7,47,9);
#Pocket := Group(pH,pB,pA,pP,pG,pD);

G := Rubik ;;
GG := "Rubik" ;;
J := Iso ;;
JJ := "J" ;;

Jcjg := Sum(J,f -> Size(Centralizer(G,f))) / Size(J);;
Print("\n\n ",GG," = ", Size(G), "\n" );
Print("\n ",JJ,"-cjg = ", Jcjg, "\n" );

1 2 3 4 5 [6] 7 8

Accueil

DMJ: 09/02/2024