Problème de non-résolubilité du Master Skewb
30
Juil
2014
Préface
Auteur: morphocode
Année: 2014
Le Master Skewb ressemble beaucoup au RexCube, c'est un RexCube sans sommets. Pour sa résolution
on peut donc d'abord utiliser l'algorithme du RexCube: RexCube = Arêtes => Centres => Pétales
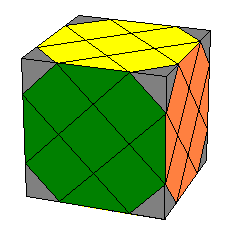 |
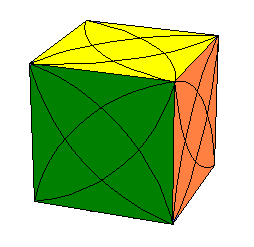 |
| Master Skewb |
RexCube |
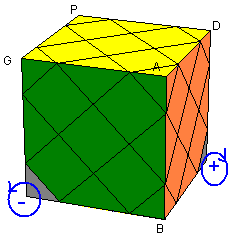
et après on range les sommets . On place les sommets Haut comme il le faut (les sommets Bas seraient automatiquement bien placés),
puis on les oriente
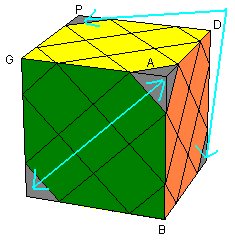 |
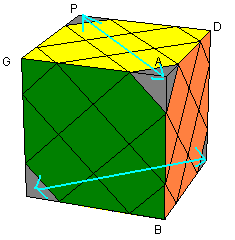 |
| Monter les sommets: [DG' ][D' B] |
Permuter les sommets: [BD' ][B' G] |
 |
|
| Pivoter les sommets: [DG' ]3 tH² [DG' ]3 (tH²=tourner le cube entier suivant H²) |
|
Mais alors il arrive parfois (mais pas toujours) un phénomène bien étrange: la non-résolubilité !!, en effet
avec l'algorithme RexCube, il arrive parfois que le cube se trouve dans un état non-résoluble (impossible de mettre les sommets en place) !!
donc de temps en temps ça marche, et de temps en temps ça ne marche pas !!! , cela nous mène aux questions suivantes:
1. Dans un état donné, comment est on sûr à 100% que c'est non-résoluble ?
2. Dans un état donné, comment est on sûr à 100% que c'est résoluble ?
3. Quelle est la probabilité de tomber dans le cas non-résoluble ?
4. Quelle est la cause de ce phénomène ? càd qui est ce qui fait que le cube est non-résoluble ?
J'avoue que j'ai du mal à comprendre ce phénomène, contrairement au problème de parité qui est plutôt facile à comprendre.
Comment ça fait que parfois l'algorithme RexCube résolve le cube , parfois non ? et dans quel cas on est sûr à 100% que RexCube marche
et dans quel cas on est sûr à 100% que RexCube ne marche pas ?
L' algorithme RexCube
L'algorithme RexCube: Arêtes => Centres => Pétales
.::ICI::.
A.
On va analyser l'algorithme RexCube
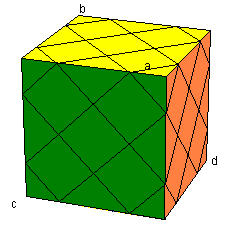
Ce qui nous intéresse ici , ce sont les 4 sommets: E={a,b,c,d}.
Durant la résolution on utilise les commutateurs (son inverse, la conjugaison et la puissance), ces commutateurs permutent 2 couples de sommets, u = (a,b)(c,d)
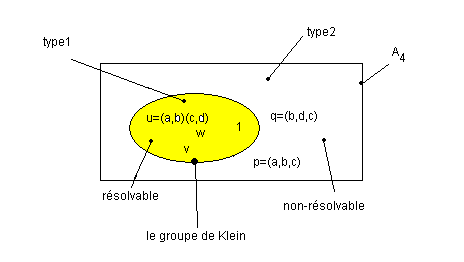
disons les permutations paires de type1 (les permutations paires de type2 sont p=(a,b,c) ; q=(b,d,c) etc .... les 3-cycles)
ce genre de permutations il y en a 3:
u = (a,b)(c,d)
v = (a,c)(b,d)
w = (a,d)(b,c)
un rapide calcule nous donne :
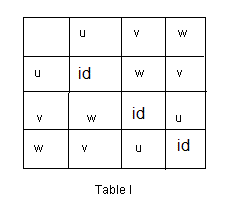 |
 |
| id = identité |
Les 4 sommets concernant |
Pendant la résolution on utilise aussi la conjugaison, mais on tombe toujours sur u,v ou w en effet on a la formule suivante:
kuk
-1 = k(a,b)(c,d)k
-1 = (k(a),k(b)) (k(c),k(d)) c'est un truc de type1
B.
Analysons l'état du cube
Une fois mélangé, les sommets {a,b,c,d} subis une permutation paire car une rotation de base gènère une permutation paire
Cas0: 0 sommets bien placé ==> possible
Cas1: 1 sommets bien placé ==> possible
Cas2: 2 sommets bien placés ==> impossible car la permutation doit être paire
Cas3: 3 sommets bien placés ==> impossible le 4ème est forcement bien placé.
Cas4: 4 sommets bien placés ==> possible
On doit donc étudier les cas: cas0, cas1,et cas4
Et voila, maintenant nous sommes en mesure de répondre à nos questions.
Question1. Dans un état donné, comment est on sûr à 100% que c'est non-résoluble ?
Reponse1: Dans le cas1, le cube est non-résoluble en effet dans ce cas le mélange résume une permutation de la forme
p = (a,b,c) = a->b->c qui laisse fixe un sommet d (sommet bon), comme l'agorithme n'utilise que les permutations du type u=(a,b)(c,d)
La résolution signifie qu'on doit avoir pu=id (id = état résolu)
donc
pu=id
pu=u² (car u²=id)
pu=uu
puu
-1=uuu
-1
p=u !!! imposible
car u bouge 4 sommets ne laisse fixe personne.
finalement quand on est dans le cas1 , RexCube ne donne jamais l'état identique (impossible de placer les sommets) on est sûr à 100% que le cube est non-résoluble.
En Rubik's Cube, on a [DH] qui permute 2 couples de sommets (a,b)(c,d) et on la transforme en une autre [DH]G'[HD]G en un 3-cycle (c,d,e)
on pense à priorie qu'on peut faire la même chose ici transformer (a,b)(c,d) en (c,d,e) mais c'est impossible car on n'a que 4 points !
Une remarque: si on fait pu on tombe forcement sur le type2, en effet si on tombe sur le type1 on aura une contradition:
pu=v (par exemple)
puw=vw (multiplier à droite, respecter l'ordre)
pv=vw
pvv
-1=vwv
-1
p = vwv
-1 (c'est un truc de type1 donc impossible car p est de type2)
Question2. Dans un état donné, comment est on sûr à 100% que c'est résoluble ?
Reponse2: Dans le cas4, et cas0 le cube est résoluble en effet dans ces cas le mélange résume à une permutation de la forme
u = (a,b)(c,d) qui permute 2 couples de sommets, pour avoir l'état identique il suffit de faire u²=id (ou v², w²)
Question3. Quelle est la probabilité de tomber dans le cas non-résoluble ?
Reponse3: on a 1/3 tomber dans le cas non-résoluble
Question4. Quelle est la cause de ce phénomène ? càd qui est ce qui fait que le cube est non-résoluble ?
Reponse4: On a 2 types de permutations paires pour les 4 sommets: C'est quand le résultat du mélange mène l'état des sommets dans le type2, RexCube ne peut pas résolver le cube
 |
|
| 2 types de permutations paires |
|
On a pu répondre à nos 4 questions grâce aux propriétés de la table I.
Ces propriétés connus sous le nom de groupe, les éléments K={id,u,v,w} forme un groupe que l'on nomme Groupe de Klein
Si on observe bien on peut représenter la table I par seulement 2 symboles u et v et 2 relations:
1. u²=v²=id
2. uv=vu
autrement dit à partir de ces 2 relations on peut remplir la table I, ces relations sont en quelque sorte un .zip de la table I
c'est plus court, plus joli, mais plus concentré et difficile à comprendre. C'est sûr le tableau I c'est plus claire, plus simple à comprendre, mais c'est plus long
Finalement la résolution du RexCube se fait par le Groupe de Klein !!
[1]
Accueil
DMJ: 20/04/2021










