L'étude théorique du Square-1

Les formules du Square-1

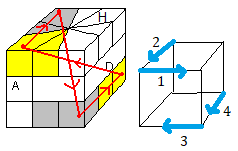
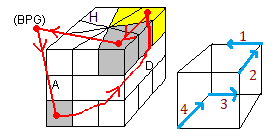
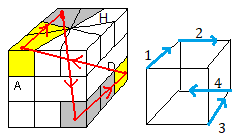
Considèrons maintenant les 4 formules suivantes:

S = 1/3/-1	Q = 1/3B/-1

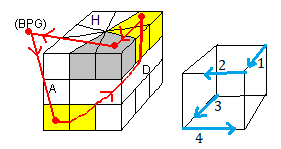E = -B/3/B	T = -B/3B/B

Par définition, les formules {3, 3B, S, Q, E, T} seront nommés "rotation standard" du Square-1 , c'est simplement une appellation . Soit M l'ensemble des formules engendrées par ces 6 rotations standards
M = < 3, 3B, S, Q, E, T >

exemple des éléments de M:
-S = 1/-3/-1 (lire à l'envers et "+" <=> "-")
S+S = 2S = (1/3/-1) + (1/3/-1) = 1/3/+/3/-1 = 1/6/-1
-Q = 1/-3B/-1
2E = -B/6/B
etc...

On pose : M⁺ = < 3, 3B, S, Q, E, T, Ω >
où Ω = (HA,HD)

Le groupe (cubique) du Square-1

On remarque que les sommets et les arêtes n'ont pas d'orientations, et il y a 8 sommets qui peuvent déplacer partout en restant dans leur camps, on a donc l'affaire avec S₈, de même pour les arêtes, finalement on pose :
G⁺ = S₈ x S₈

Quand on applique une formule V∈M sur le Cube (forme cubique), on passe d'une configuration à une autre, M agit donc sur G⁺
On définit une action '•' de M dans G⁺ ainsi
G⁺ x M --> G⁺
(s,V) --> s•V = t
Vérifiant les axiomes suivants:
A₁ : s•I = s
A₂ : (s•V)•T = s•(VT)
A₃ : a donné,fixé
a•V = a ==> V=I
A₄ : s•(VT) = (s•V)(s•T)

Considèrons maintenant G l'ensemble des états produits par M (gènérés par M) c'est par définition le groupe (cubique) du Square-1.
G = {µ∈G⁺ | µ=e•V , V∈M}
G provient de M = < 3, 3B, S, Q, E, T >
Comme un état se réduit à une permutation donc les éléments de G sont des permutations.

et G est contenu dans S₈ x S₈
G ⊂ G⁺ = S₈ x S₈
Comme les arêtes et les sommets ne s'entremèlent pas; G est composé de deux trucs indépendants:
G = G_a x G_s ; G_a = arêtes et G_s = sommets

Donc une formule gènère deux permutations: une pour les arêtes u, et l'autre pour les sommets v, le couple (u,v) est un élément de G , u ∈ G_a, v ∈ G_s Nous allons montrer que le Square-1 possède une loi de "parité", plus précisement la loi des phases.

NOTE : G⁺ est le groupe étendu de G, G⁺ = S₈ x S₈, G ⊂ G⁺
Il faut absolument faire la distinction entre M et G , M = formules = mouvements = mélanges et G = états = configurations = motifs

A₈ x A₈ ⊂ G

On commence par s'occuper les arêtes, pour les sommets c'est pareil

A1. Trouver un 3-cycle dans G_a (arêtes) .
On pose
Z = (-B/6/B)-3B+(1/6/-1)+6B+(-B/3/B)+6B
Z = 2E-3B+2S+6B+E+6B.
à partir de Z et 3, on peut fabrique un O telle que
e•O = (u,id) ; u =(x₁,x₂,x₃)
Plus précisement
O = -3+Z-3+Z+6.
(x₁,x₂,x₃) = O = -3+(2E-3B+2S+6B+E+6B)-3+(2E-3B+2S+6B+E+6B)+6 .

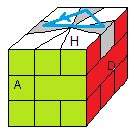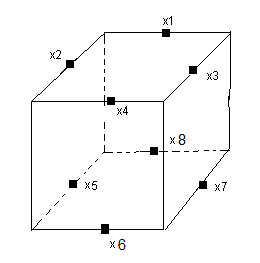
Les arêtes numérotées	O

La formule O gènère une permutation u dans G_a avec u = (x₁,x₂,x₃), comme les sommets ne bougent pas on a v=id (identité)

A2. Trouver une famille particulière de permutations de G_a

On veut trouver une famille particulière (x₃,x, ... ) de permutations de G_a qui laissent fixe x₁,x₂ où x est une arête différente de x₁,x₂,x₃ , ces permutations peuvent bouger les autres pièces

Ce n'est pas bien compliqué , il sufit de prendre les kT combiné avec 3B on aura tout ce qui faut !!!
Par exemple T = -B/3B/B qui donne comme permutation sur les arêtes t=(x₃,x₄,...) et laisse x₁,x₂ fixes
et de même 2T ==> une permutation t²=(x₃,x₅,...) et x₁,x₂ fixes ainsi on peut donc (avec 3B) remplacer l'arête x par x₄, x₅, ...

A3. Trouver une famille (x₁,x₂,x) de G_a
On veut trouver une famille de permutations de G_a du type (x₁,x₂,x) où x₁,x₂ sont données et x est une arête différente de x₁,x₂ . Ici on va utiliser une propriété très connnue des permutations

Propriété : Soient p une permutation et (a,b,c) un 3-cycle alors on a:
p^-1(a,b,c)p = ( p(a), p(b), p(c) )

Nous allons donc appliquer cette propriété dans notre cas.
t^-1ut = t^-1(x₁,x₂,x₃)t = ( t(x₁),t(x₂),t(x₃) )= ( x₁,x₂,x₄ )
t^-2(x₁,x₂,x₃)t² = ( t²(x₁),t²(x₂),t²(x₃) )= ( x₁,x₂,x₅ )
....
Ainsi la famille (x₁,x₂, x) où x₁,x₂ sont données, et x=x₃, x₄, x_5,...
sont des 3-cycles dans G_a car ils proviennent de M
Or on sait que cette famille engendre A₈ donc A₈ ⊂ G_a

On fait la même chose avec les sommets.

B1. Trouver un 3-cycle dans G_s (sommets).
On pose
X = (1/3/-1)-3B+(1/3/-1)-3+(1/-3+3B/-1)
X = S-3B+S-3-S+Q
à partir de X et 3 on peut fabriquer une formule C de G telle que
e•C=(id,v) ; v=(y₁,y₂,y₃)
Plus précisement
(y₁,y₂,y₃) = C = 6+X-6 = 6+S-3B+S-3-S+Q-6

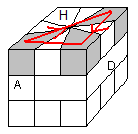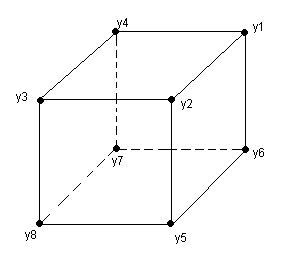
Les sommets numérotés	C

C gènère une permutation v = (y₁,y₂,y₃) dans G_s et u=id les arêtes ne bougent pas

B2. Trouver une famille particulière de permutations de G_s

On veut trouver une famille particulière (y₃,y, ... ) de permutations de G_s qui laissent fixe y₁,y₂ où y est un sommet différent de y₁,y₂,y₃ , ces permutations peuvent bouger les autres pièces

On prend les kS combiné avec 3B on aura tout ce qui faut !!!
Par exemple S=1/3/-1 qui donne comme permutation sur les sommets s=(y₃,y₄,...) et laisse y₁,y₂ fixes
et de même 2S ==> s²=(y₃,y₅,...) et y₁,y₂ fixes ainsi (avec 3B) on peut remplacer le sommet y par y₄ ,y₅ ...

B3. Trouver une famille (y₁,y₂,y) de G_s

On veut trouver une famille de permutations de G_s du type (y₁,y₂,y) où y₁,y₂ sont donnés et y est un sommet différent de y₁,y₂
s^-1vs = s^-1(y₁,y₂,y₃)s = (y₁,y₂,y₄)
s^-2(y₁,y₂,y₃)s² = (y₁,y₂,y₅)
....
Ainsi la famille (y₁,y₂, y) où y₁,y₂ sont donnés, et y=y₃, y₄, y_5,...
sont des 3-cycles dans G_s car ils proviennent de M
Or on sait que cette famille engendre A₈ donc A₈ ⊂ G_s

En résumé:
A₈ ⊂ G_a
A₈ ⊂ G_s
A₈ x A₈ ⊂ G_a x G_s = G

G ⊂ Ker(f)

Soit f défini par:
f : S₈ x S₈ -> {1,-1}
(u,v) -> f(u,v) = sig(u).sig(v)
Ker(f) = { (u,v)| sig(u).sig(v) = 1 }

Les formules: {3, 3B, S, Q, E, T} ont toutes des permutations impaires pour des arêtes ainsi que pour des sommets ,
donc sig(u).sig(v) = (-1).(-1) = 1 donc elles sont toutes dans le Ker(f), par conséquence G aussi
G ⊂ Ker(f)
finalement
A₈ x A₈ ⊂ G ⊂ Ker(f)

Rappel sur les indices:
K ⊂ H ⊂ G
[G:K] = [G:H][H:K]
[GxG':HxH'] = [G:H][G':H']

A₈ x A₈ ⊂ G ⊂ Ker(f) ⊂ S₈ x S₈
[S₈ x S₈:A₈ x A₈]=[S₈ x S₈:Ker(f)][Ker(f):A₈ x A₈]
[S₈:A₈] x [S₈:A₈]=[S₈ x S₈:Ker(f)][Ker(f):A₈ x A₈]
2 x 2 = 2 x [Ker(f):A₈ x A₈]
2 = [Ker(f):A₈ x A₈]

Mais entre A₈ x A₈ et Ker(f) il n'y a rien parce que l'indice de [Ker(f):A₈ x A₈] vaut 2
donc on a:
- soit: G = A₈ x A₈
- soit: G = Ker(f)
Comme S engendre 2 permutations u (pour les arêtes), v (pour les sommets) impaires,
(u,v) ∉ A₈ x A₈ => G ≠ A₈ x A₈ donc G = Ker(f)
Ca signifie sig(u).sig(v)=1 c'est à dire u pair ==> v pair , u impair ==> v impair
La loi des phases (les sommets et les arêtes sont en phases) est ainsi démontrée...

Finalement, le théorème fondamental :
G = { (u,v)∈S₈xS₈| sig(u) = sig(v) }

Remarque: on a: (S₈ x S₈) / Ker(f) = Im(f) donc
|S₈ x S₈| / |Ker(f)| = |Im(f)|
|Ker(f)| = |S₈ x S₈| / |Im(f)|
|G| = 8! x 8! / 2
|G| = 812 851 200

Le GAP
Télécharger le GAP .::ICI::. https://www.gap-system.org/Releases/4.4.12.html
Dans la fenêtre de cmd on se place dans le dossier de GAP
C:\Users\nom> cd\gap4r4\bin
C:\gap4r4\bin>gap < gap_sqr.txt

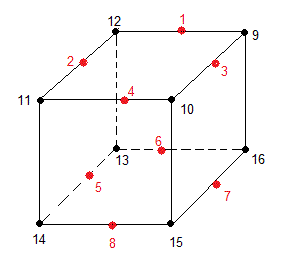numérotation des pièces

gap_sqr.txt:

#gap_sqr.txt
#12 1 9
#2 H 3
#11 4 10
#---------
#13 6 16
#5 B 7
#14 8 15

p3 := (1,3,4,2)(9,10,11,12) ;
p3B := (5,8,7,6)(13,14,15,16) ;
pS := (2,8,7,4)(12,15,16,11) ;
pQ := (1,3,6,5)(9,10,13,14) ;
pE := (2,1,7,6)(11,12,15,16) ;
pT := (3,4,5,8)(9,10,13,14) ;
pOmega := (4,3);
LAMBDAPLUS := Group(p3, p3B, pS, pQ, pE, pT, pOmega);
# SLAMBDAPLUS := Size( LAMBDAPLUS );
LAMBDA := Group(p3, p3B, pS, pQ, pE, pT);
# SLAMBDA := Size( LAMBDA );
Print( "\n" );
Print( "|LAMBDA+| = ",Size( LAMBDAPLUS ), "\n" );
Print( "|LAMBDA| = ", Size( LAMBDA ) , "\n" );
Print( "N = ", 2 , "\n" );
Print( "|G+| = ", Factorial(8) * Factorial(8) , "\n" );
Print( "|G| = |G+|/N = ", (Factorial(8) * Factorial(8)) / 2 , "\n" );

Le GAP nous donne bien :
|G⁺| = 1625702400
|G| = 812851200
indice = |G⁺|/|G| = 2

Problème de parité

Pour comprendre la parité du Square-1, observons la parité de l'Helicopter Cube.

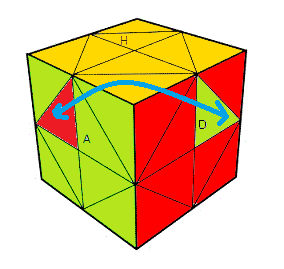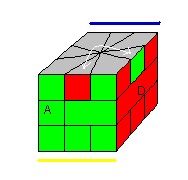Parité d'Helicopter	Parité du Square-1

Le problème de parité d'Helicopter s'explique assez bien:
On a un ensemble de rotations standard (de base) : {A,D,G,P, ...} à 180° et un ensemble de rotations non-standard, rotations-jumbling, rotations cachées ...{a,d,g,p, ... } à 60°. Lorsqu'on mélange l'Helicopter avec les rotations non-standard , il peut arriver d'avoir une "parité", donc la cause du problème de parité chez l'Helicopter provient de l'utilisation des rotations non-standard.

Eh bien chez le Square-1 c'est pareil, le problème c'est qu'il faut trouver ceux qui sont les rotations standard et non-standard chez le Square-1.
Pour le square-1 on a:
Rotations standard: {3, 3B, S, Q, E, T}
Rotations non-standard: {1, B, /}

Observons bien les rotations standards, elles vérifier la loi "de parité", "en phase" :
Helicopter : Les sommets et les feuilles (d'une orbite) sont en phase : sig(sommets) = sig(feuilles_une_famille)
Square-1 : Les sommets et les arrêtes sont en phase : sig(sommets) = sig(arrêtes)
et lorsqu'on utilise le rotations non-standard il peut arriver qu'on viole cette loi donc ==> "problème de parité"

Pour un état s quelconque du Cube on a :
a. non-cubique,impair
b. non-cubique,pair
c. cubique,impair => problème de parité (par définition)
d. cubique,pair => normal, légal

Donc parler de la parité il faut fixer, préciser ceux qui sont les rotations standards (rotations de base), et vérifie que les rotations standards donnent une loi de parité du genre:
==> sig(sommets) = sig(arêtes) ;en phase
==> sig(sommets) = sig(arêtes) = 1
....

Probabilité d'avoir une parité
On pourrait se demander quelle est la probabilité de tomber dans le problème de parité ?
-Avant de passer à la forme cubique on est dans un état µ soit pair soit impair
-On passe à la forme cubique par une formule F, soit pair, soit impair
d'où l'arbre de probabilité

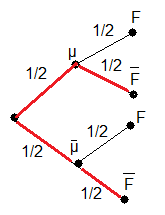l'Arbre de probabilité

d'où

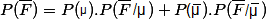
= 1/2 . 1/2 + 1/2 . 1/2 = 2/4 = 1/2
On a 50% de chance d'avoir la parité

Fixer la parité

Un état de parité s c'est un élément qui n'est pas dans G, s ∉ G, pour fixer la parité, on est donc obligé d'utiliser quelque part les rotations non-standard {1, B, /}

A. Première méthode
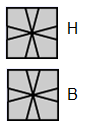
On casse la forme cubique, rendre l'état pair puis revenir à la forme cubique.

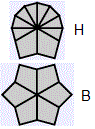I. Forme cubique ===>	II. forme Roue ===>

===> III. forme cubique

Pour voir il suffit de passer à la forme Roue (f0) à partir de l'état résolu (pair), puis on fait 2B (rotation de l'étoile = permutation impaire des sommets) puis on revient à la forme cubique, là le twist sera en état impair, et on aura donc un problème de parité, autrement dit il suffit que le twist soit en état impair avant de passer à la forme cubique, on aura un problème de parité.

Finalement le problème de parité de Square-1 provient au moment où l'on remonte toutes les arêtes vers le Haut (la forme roue) pour passer à la forme cubique. En fin compte c'est assez logique que la parité se produit pendant cette phase. En effet , les arrêtes et les sommets sont remontés de façon arbitraire , ils ne suivent peut-être plus la loi des phases... et comme vous le savez dèsqu'il y a de l'arbitraire on risque d'avoir la parité ...

Pour bien comprendre les choses, prenez votre Square-1 à l'état résolu, puis appliquez cette formule.
/-3-3B/2+B/-2-4B/ ; formule pair
Vous tombez sur la forme Roue, obsevez bien la disposition des pièces, si vous faites 2B, les sommets et les arêtes ne sont plus en phases (sommets = permutation impaire, arêtes = immobiles = permutation paire) donc si vous revenez à la forme cubique maintenant vous aurez un problème de parité!
autrement dit

1. Cube -> Roue : /-3-3B/2+B/-2-4B/ ; pair
2. Permutation impaire des sommets : 2B (6-cycle)
3. Roue -> Cube : /2+4B/-2-B/3+3B/ ; pair

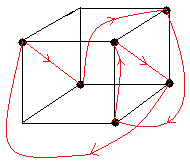6-cycle sommets => impair

B. Deuxième méthode
Pour fixer la parité, on va transformer l'état impair du cube en état pair par les formules ci-dessous
tenir le cube: (HA)<->(HD)
W = (/ 3+3B/ 1+2B/ 2+2B/ 2/ 2+2B/ 1+2B/ -3-3B/) + (1/ 3+3B/ -1-B/ 3+3B/-2B)
ou bien
F = 1/ 2+2B/ -2B/ 3+3B/ 1/ 4+4B/ -2B/ 2+2B/ -B/ 3+3B/

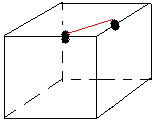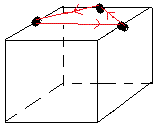état impair	état pair

Résumons nous:

1. Lorsqu'on mélange le Cube avec les rotations {1,B,/} on arrive à l'un des 4 états ci-dessous
a. non-cubique,impair
b. non-cubique,pair
c. cubique,impair => problème de parité (par définition)
d. cubique,pair => normal, légal

2. Théorème : Le groupe G de Square-1 c'est l'ensemble des configurations µ=(u,v) vérifiant sig(u)=sig(v)
G = { µ=(u,v)∈S₈xS₈| sig(u) = sig(v) }

3.Lorsqu'on mélange le Cube avec les rotations {1,B,/} il arrive parfois que l'état du Cube soit impair, puis on passe à la forme cubique en gardant cet état ainsi on a un probleme de parité.

4. Pour fixer la "parité" on a plusieurs méthodes
Première méthode
Le principe est simple: de la forme Cube on passe à une autre forme, puis on fait une permutation impaire des sommets, et on revient à la forme Cube, le twist est maintenant en état pair.
Exemple:

Cube ==> Roue (/-3-3B/2+B/-2-4B/) ; pair
2B ; sommets impair
Roue ==> Cube (/2+4B/-2-B/3+3B/) ; pair
Résoudre de nouveau le cube. (sommets et arêtes sont maintenant en phase)

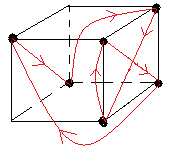6-cycle sommets

Deuxième méthode
On rend le cube en état pair grâce à la formule ( tenir le cube: (HA)<->(HD) )
W = (/ 3+3B/ 1+2B/ 2+2B/ 2/ 2+2B/ 1+2B/ -3-3B/) + (1/ 3+3B/ -1-B/ 3+3B/ -2B)
ou bien
F = 1/ 2+2B/ -2B/ 3+3B/ 1/ 4+4B/ -2B/ 2+2B/ -B/ 3+3B/

5. Finalement la causalité de la "parité" chez le Square-1 est plus subtile que chez l'Helicopter, plus difficile à comprendre, à cause des rotations standards à trouver chez le Square-1

Le mélange peut donner un état impair à la forme cubique, qui viole ainsi la loi des phases on aura donc un problème de parité !!!
En conclusion: La difficulté c'est de trouver les rotations standars possédant la loi des phases, c'est-à-dire de trouver les rotations
M = < 3, 3B, S, Q, E, T >.

Conclusion Cette étude théorique du Square-1 permet d'avoir un algorithme de résolution du Square-1 (on est sûr de s'en sortir à 100%)
Algorithme

1. On passe de la forme non-cubique à la forme cubique par les 5 formules .
   f₀ = /2+4B/-2-B/3+3B/
   f₁ = /-2/3-4B/-2/
   f₂ = /-2B/2
   f₃ = /-2B/-4
   f₄ = /2/
   
2. Si le Cube a un état impair, on utilise la formule W ou F pour le transformer en état pair .
3. On résoud le Cube

L'Algorithme VIP:

Lorsque le Cube est en état cubique-pair, alors on peut résoudre le Cube par M = < 3, 3B, S, Q, E, T >. Voici l'algorithme s'exprimant avec ces 6 formules (très précieuses) :

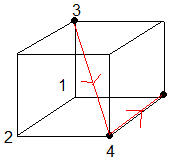
S = 1/3/-1 ==> Descendre un sommet

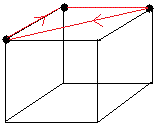
X = 1/3/-3B/3/-3/-3+3B/-1 = (1/3/-1)-3B+(1/3/-1)-3+(1/-3+3B/-1) = S-3B+S-3-S+Q ==> 3-cycle-sommet

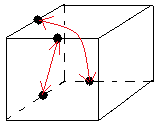
Y = -B/6/4B+1/6/-1+5B/-3/7B = (-B/6/B)+3B+(1/6/-1)+6B+(-B/-3/B)+6B = 2E+3B+2S+6B-E+6B ==> Descendre 2 arêtes

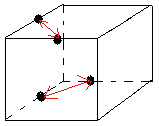
Z = -B/6/-2B+1/6/-1+5B/3/7B = (-B/6/B)-3B+(1/6/-1)+6B+(-B/3/B)+6B = 2E-3B+2S+6B+E+6B ==> Permuter 2 arêtes-Haut, 2 arêtes-Bas

S	X

Y	Z

L'algorithme:

1. Ranger les sommets Bas: S, 3, 3B : on place les sommets 1,2 puis 4 à la place du 3, puis on place le 3 qui pousse le 4 à sa place
2. Ranger les sommets Haut: : X, 3 (Si les sommets sont en état impair on fait un 3)
3. Ranger les arêtes Bas: Y, 3, 3B (on forme les arêtes-adjacentes-Bas)
4. Ranger les arêtes Haut: Z, 3

Un théorème

Théorème: Une configuration µ=(u,v)∈G⁺ est un état (µ∈G) ssi sig(u) = sig(v)

Démo :
¤ On se donne une formule V∈M telle que e•V=µ=(u,v), il faut montrer que sig(u)=sig(v)
Chaque rotation de base gènère un 4-cycle-arête a et un 4-cycle-sommet b donc
sig(a)=sig(b)
par suite pour une formule V on a bien sig(u)=sig(v)

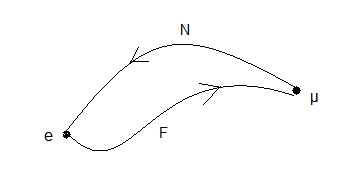
¤ On se donne un état µ=(u,v) avec sig(u)=sig(v) (µ∈G) , il faut trouver une formule V∈M telle que e•V=µ
comme sig(u)=sig(v) l'algorithme VIP permet de résoudre le Cube càd trouver une formule N∈M telle que
µ•N=e
il suffit de prendre V=-N et on aura
e•V=µ ; µ provient donc de M

-N=F

[1] 2

Accueil

DMJ: 03/11/2024