Loi interne de (G,.)
28
Jui
2013
Introduction ...
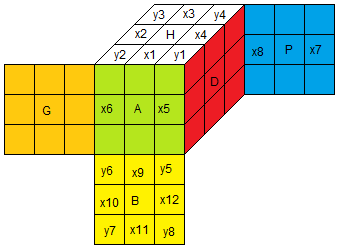
Le but est définir une loi de composition '.' sur G, pour décrire exactement ce qui se passe sur le Rubik's Cube.
Par définition : G = {s∈G+ / s=e•V , V∈M}
Définition la loi '.' dans (G,.)
On sait (th fondamental de la Cubologie) que G est l'ensemble des éléments (u,x,v,y) de
G
+ = S
12 x Z
212 x S
8 x Z
38 vérifiant:
(F) ∑ x
i = 0 (mod 2) en abrégeant x=0 (mod 2) avec x = (x
1,x
2,...,x
12)
(T) ∑ y
i = 0 (mod 3) en abrégeant y=0 (mod 3) avec y = (y
1,y
2,...,y
8)
(P) sig(u) = sig(v)
Une loi '.' définie sur G doit permettre de démontrer les 3 propriétés ci-dessus, qui caractisent le Rubik's Cube, sinon ça sert à rien d'avoir une loi sur G !!
Voyons d'abord sur les arêtes
On a un ensemble de arêtes qui baladent partout dans leur camp, et en baladant elles peuvent changer leurs orientations. Il faut donc définir une loi
qui correspond avec le mouvement commposé. Par ex pour les arêtes, la rotation A gènère un état (p,a) et D gènère (p',a')
A --> (p,a)
D --> (p',a')
AD --> (p,a)(p',a') = (u,x) ??
Il faut donc définir une loi '.' qui doit correspondre avec le résultat des rotations AD
Remarque : on a, u = pp' (p' o p) c'est évident car on fait A puis D
Définition x' = a + p(x)
 |
|
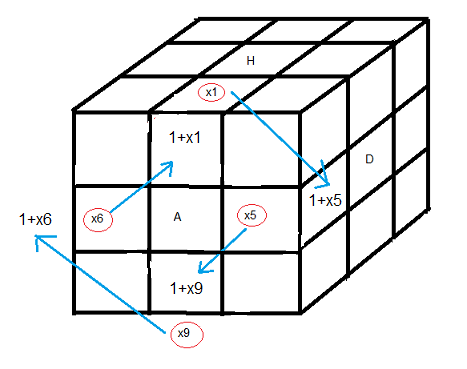
| flèche bleue: x'1 = 1+x5 |
|
Suivons le mouvement des flèches bleues (flèche partant), le x
1 arrive (il bouge) à la facette 1+x
5 et prend cette valeur
càd x'
1 = 1+x
5
x
1 dans (HA) se place dans (AD) en 1+x
5
x'
1 = 1+x
5
x'
5 = 1+x
9
x'
9 = 1+x
6
x'
6 = 1+x
1
x' = a + p(x) avec p=(1,5,9,6) et a=(1,0,0,0,1,1,0,0,1,0,0,0)
Donc ce qui suggère de définir -pour les arêtes- la loi '.' dans G ainsi:
(p,a)(p',a') = (pp', a + p(a'))
u = pp'
x = a+p(a')
Vérifions si ça correspond bien
*Pour A on a: A --> (p,a) avec
p = (1,5,9,6)
a = (1,0,0,0,1,1,0,0,1,0,0,0)
*Pour D on a: D --> (p',a') avec
p' = (4,8,12,5)
a' = 0
AD --> (p,a)(p',a') = (pp', a + p(a') )
pp' = (1,5,9,6)(4,8,12,5) = (4,8,12,5,9,6,1)
p(a') = 0
a + p(a') = (1,0,0,0,1,1,0,0,1,0,0,0)
AD --> (u,x) avec u=(4,8,12,5,9,6,1) et x=(1,0,0,0,1,1,0,0,1,0,0,0)
Pour les arêtes, c'est exactement ce qui se passe sur le Rubik's Cube !!!
Définition y' = b + q(y)
On a un ensemble de sommets qui baladent partout dans leur camp, et en baladant ils peuvent changer leurs orientations. Il faut donc définir une loi
qui correspond avec le mouvement commposé. Par ex pour les sommets, la rotation A gènère un état (q,b) et D gènère (q',b')
A --> (q,b)
D --> (q',b')
AD --> (q,b)(q',b') = (v,y) ??
Il faut donc définir une loi '.' qui doit correspondre avec le résultat des rotations AD
Remarque : on a, v = qq' c'est évident car on fait A puis D
Observons la fig ci-dessous
 |
|
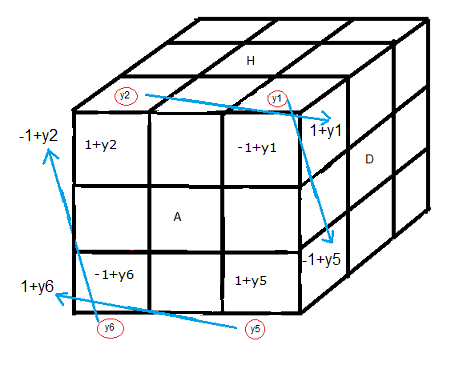
| flèche bleue: y1' = 1+y5 |
|
Suivons le mouvement des flèches bleues (flèche partant), le y
1 arrive (il bouge) à la facette -1+y
5 et prend cette valeur
càd y'
1 = -1+y
5
y
1 dans (HDA) il se place dans (BAD) en -1+y
5
y'
1 = -1+y
5
y'
2 = 1+y
1
y'
5 = 1+y
6
y'
6 = -1+y
2
y' = b + q(y) avec q=(1,5,6,2) et b=(-1,1,0,0,1,-1,0,0)
Donc ce qui suggère de définir -pour les sommets- la loi '.' dans G ainsi:
(q,b)(q',b') = (qq', b + q(b'))
v = qq'
y = b+q(b')
Vérifions si ça correspond bien
*Pour A on a: A --> (q,b) avec
q = (1,5,6,2)
b = (-1,1,0,0,1,-1,0,0)
*Pour D on a: D --> (q',b') avec
q' = (1,4,8,5)
b' = (1,0,0,-1,-1,0,0,1)
AD --> (q,b)(q',b') = (qq', b + q(b') )
qq' = (1,5,6,2)(1,4,8,5) = (2,4,8,5,6)
b = (-1,1,0,0,1,-1,0,0)
q(b') = (-1,1,0,-1,0,0,0,1)
b + q(b') = (1,-1,0,-1,1,-1,0,1)
AD --> (v,y) avec v=(2,4,8,5,6) et y=(1,-1,0,-1,1,-1,0,1)
Pour les sommets, c'est exactement ce qui se passe sur le Rubik's Cube !!!
Finalement la loi de composition '.' dans G est donc
(u, x, v, y)(u', x', v', y') = ( uu', x+u(x'), vv', y+v(y') )
où
uu' = u'o u
u(x) = (x
u(1), x
u(2), ...,x
u(n)) ;u=permutation, x=vecteur
1 2 3 4 5 6 7 [8]
Accueil
DMJ: 28/05/2025