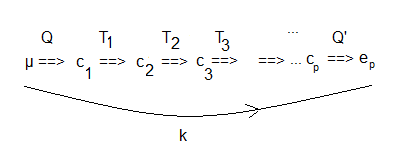Les groupes d'homotopie du Square-1

Un simple MOD

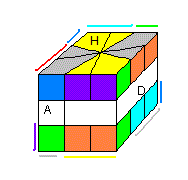
J'ai donc transformé (un MOD) un Square-1 en forme Papillon (fig 1) , c'est jolie et c'est assez simple à le faire , il suffit de couper l'équateur en forme de Papillon et cacher les trous c'est tout. Une fois le MOD est réalisé, une simple question se pose immédiatement: Comment le résout-on ?
Faudrait-il trouver de nouvelles formules qui déplacent les pièces en conservant la forme Papillon ?, comme pour la forme "Cube" - Les formules de résolution conservent la forme cubique du puzzle -

fig1

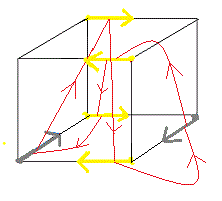
Une petite réflexion et la réponse est prèsqu'immédiate, à partir de la forme Papillon on passe à la forme cubique, on le résout en respectant les couleurs de Papillon , puis on revient à la forme Papillon
Papillon (-3B/3+3B/-3) => Cube => résoudre => Cube (3/-3-3B/3B) => Papillon

On voit donc les nouvelles formules pour Papillon sont des conjugaisons de formules cubiques.

ep : Etat résolu du Papillon	/3+3B/-3

Les Groupes d'homotopie du Square-1

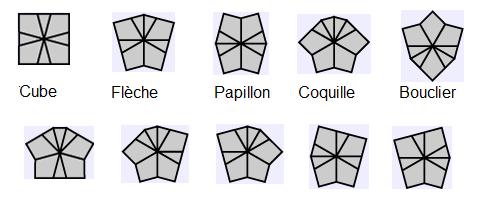
Chaqu'un sait que pour résoudre le Square-1 on doit passer par sa forme "Cube", et la résolution démarre donc par la forme cubique du puzzle. Si on impose le Haut ayant 4 sommets et 4 arêtes (comme la forme Cube) on trouve 10 formes suivantes (même chose pour le Bas) que l'on nomme les 10 formes homotopes du Square-1

10 formes pour le Haut

Rappel : Soient H et K deux sous groupes de G, on dit que H et K sont conjugués si:
∃q ∈ G tel que qHq^-1 = K
autrement dit
∃q ∈ G tel que ∀x∈H , qxq^-1 ∈ K

On considère maintenant les mouvements P₀ du twist qui conservent la forme Papillon et pairs. L'ensemble des états produits par P₀ (gènérés par P₀), forme un groupe c'est le groupe Papillon du Square-1 ou le 3ème groupe d'homotopie et on le note H₃. Le groupe du Square-1 est le groupe 1er groupe d'homotopie, H₁.
et si on pose Q = 3/-3-3B/3B et q la permutation associée à Q , alors on a la relation suivante:
H₃ = qH₁q^-1


En effet , on part d'un état de Papillon µ, on passe à l'état cubique c₁ par la formule Q, puis on résout le cube par des formules T₁,T₂,T₃, ...
quand on arrive à l'état cubique c_p, là on passe à la forme Papillon par Q' et on tombe sur l'état résolu de Papillon e_p.
on a donc:
t₁t₂t₃... = t où t ∈ H₁
Soit k∈H₃ la permutation qui fait passer de l'état µ à l'état résolu e_p, (l'inverse de e_p -> µ) alors on a :
k = qtq^-1 et k ∈ H₃

c'est à dire ces 2 groupes sont conjugués (dans S₂₄) , donc on passe d'un élément de H₁ à un élément de H₃ par la conjugaison , par exemple:
Si t est un état de H₁ l'état correspondante dans H₃ est
qtq^-1

On pourrait faire la même chose sur les autres formes homotopes du Square-1 on trouve donc ainsi 10 groupes d'homotopie correspondant aux 10 formes homotopes du Square-1: Cube, Flèche, Papillon, Coquille, Bouclier, etc.... Ils sont tous conjugués entre eux.

Papillon	Coquille

1 [2]

Accueil

DMJ: 30/09/2022