Le secret du BigBlock

Entrons dans l'aventure ...

C'est vrai pourquoi n'a t-on pas besoin de permuter deux sommets-Haut ni de faire un 3-cycle pour bien placer les sommets Haut quand les 2 sommets Bas sont bien placés ?

Voyons cela de plus près :
Le BigBlock possède deux rotatations H, D qui effectent les sommets . Le groupe des formules M = < H,D > engendré par H, et D gènère un groupe nommé le groupe des sommets < H,D >_s , < H,D >_s est évidemment un sous groupe de S₆ .

La remarque précédente, provient d'une propriété mathématique très curieuse du groupe < H,D >_s découverte par D. SINGMASTER . En effet on a 6 sommets qui baladent par tout donc on s'attend à se trouver les 6!=720 permutations, càd < H,D >_s = S₆ . Et bien D. SINGMASTER a montré que < H,D >_s est beaucoup plus petit plus exactement 120 éléments au lieu de 6!=720 éléments ! et encore ce groupe à 120 est très spécial, très connu ...
< H,D >_s = PSL(2,5) = S₅

On comprend maintenant pourquoi on n'a pas besoin de permuter deux sommets, ni de faire un 3-cycle pour bien placer les 4 sommets Haut, car ce sont des configurations qu'on ne peut pas atteindre, autrement dit les 2-cycles et 3-cycles, ce ne sont pas des éléments du groupe !
< H,D >_s.

Vers un chemin difficile ...

On va placer les éléments de P(F₅) sur le BigBlock comme indique le fig ci-dessous
P(F₅) = {0,1,2,3,4, ∞ }

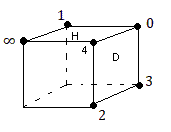
Formons nous les 5 motifs suivants:
a = { {1,0}, {∞,3}, {4,2} }
b = { {1,2}, {0,3}, {∞,4} }
c = { {∞,1}, {0,2}, {4,3} }
d = { {∞,0}, {1,4}, {2,3} }
e = { {∞,2}, {1,3}, {0,4} }
et soit E = { a, b, c, d, e } l'ensemble de ces 5 motifs

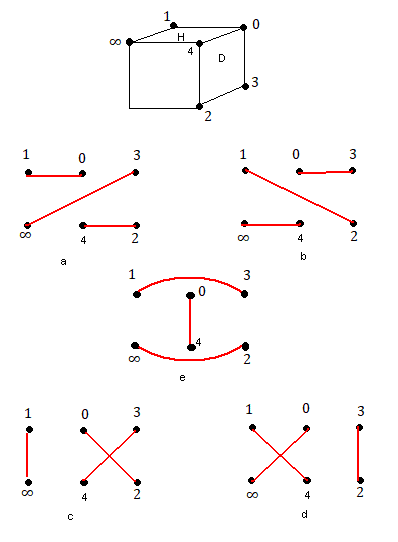
Soient p = 0->4->∞->1 et q = 0->3->2->4 les permutations associées à H et D (p,q ∈ S₆), on a donc < H,D >_s = < p,q >

Voyons l'effet de p sur E
a = { {1,0}, {∞,3}, {4,2} } • p= { {0,4}, {1,3}, {∞,2} } = e
b = { {1,2}, {0,3}, {∞,4} } • p= { {0,2}, {4,3}, {1,∞} } = c
c = { {∞,1}, {0,2}, {4,3} } • p= { {1,0}, {4,2}, {∞,3} } = a
d = { {∞,0}, {1,4}, {2,3} } • p= { {1,4}, {0,∞}, {2,3} } = d
e = { {∞,2}, {1,3}, {0,4} } • p= { {1,2}, {0,3}, {4,∞} } = b
u=a->e->b->c
c'est-à-dire a • p est un élément de E, b • p est un élément de E, etc ....

De même pour q
a • q = e
b • q = d
c • q = c
d • q = a
e • q = b
v=a->e->b->d
càd a • q est un élément de E, b • q est un élément de E, etc ....

p et q agissent sur E ( E • p = E, E • q =E ) donc le groupe < p,q > agit sur E. Maintenant nous pouvons répondre à notre question.
Supposons qu'il existe une permutation qui échange seulement 2 sommets Haut par ex r=(∞,1) alors

r=(∞,1)
a • r = { {∞,0}, {1,3}, {4,2} }
b • r = { {∞,2}, {0,3}, {1,4} }
c • r = { {∞,1}, {0,2}, {4,3} }
d • r = { {1,0}, {∞,4}, {2,3} }
e • r = { {1,2}, {∞,3}, {0,4} }

a • r ∉E,

de même pour un 3-cycle s=(0,4,1)
s=(0,4,1)
a • s = { {0,4}, {∞,3}, {1,2} } ∉E

r,s n'agissent pas sur E donc r,s ne sont pas des éléments du groupe < p,q >, c'est donc des configurations impossibles à atteindre.
Et voilà le travail, le truc c'est de trouver un objet qui laisse agir par < H,D >_s , on a trouvé E l'ensemble de ces 5 motifs ci-dessus.

Encore plus loin ...

On a répondu à notre question, mais on ne sait pas combien le < H,D >_s est petit. Voyons
La permutation p donne la permutation u = a->e->b->c de E , et q en donne une autre v = a->e->b->d , maintenant on va associer un élément de < p,q > à une permutation de < u,v > ⊂ S_E de la façon suivante:

f: < p,q > ---> < u,v >
p ---> u : f(p) = u
q ---> v : f(q) = v
C'est évidemment un homomorphisme, elle est clairement sujective , en effect on trouve toujours un antécédant par exp pour :
r = u²vuv^-1 ---> f(p²qpq^-1) = r
on va voir qu'elle est aussi injective. Comme c'est un homomorphisme il suffit de montrer que son noyau se réduit à l'identité.

f injective
Notons I l'identité de < u,v >
on prend donc t , un élément de < p,q > tel que f(t) = I (f(t) est une permutation de E, f(t) = I ça signifie que f(t) laisse E fixe: I(a)=a, I(b)=b, I(c)=c, etc ... )
rappel
a = { {1,0}, {∞,3}, {4,2} }
b = { {1,2}, {0,3}, {∞,4} }
c = { {∞,1}, {0,2}, {4,3} }
d = { {∞,0}, {1,4}, {2,3} }
e = { {∞,2}, {1,3}, {0,4} }


supposons que t(∞) = 0

dans e: t(∞) = 0 oblige t(2)=4 car I(e)=e

dans c: t(∞) = 0 oblige t(1)=2 car I(c)=c

dans b: t(1) = 2 oblige t(2)=1, car I(b)=b, mais t(2)=1 contraditoire avec t(2)=4

donc t(∞)≠0, même raisonnement montre que t(∞)≠ 1,4,2,3 seul cas possible t(∞)=∞
et le même travail donne
t(0)=0, t(1)=1, t(2)=2, t(3)=3, t(4)=4, t(∞)=∞, c'est à dire t=id, f est donc injective, et finalement elle est bijective.
Et c'est presque fini, le programme GAP donne l'ordre de |< u,v >| = 120, on a donc bien
|< u,v >| = |< H,D >_s| = 120

[1]

Accueil

DMJ: 05/07/2024