Formule, Etat

Action, Opèrer, Agir....

On pose :

(i) G⁺ = S₁₂ x Z₂¹² x S₈ x Z₃⁸
(G⁺, .) où la loi '.' : (u,x,v,y)(u',x',v',y') = (uu',x+u(x'), vv',y+v(y'))
où
uu' = u' o u
p(x) = (x_p(1) , x_p(2) ,..., x_p(n)) ; p=permutation, x=vecteur
G⁺ = l'ensemble des configurations

x_i = 0 (resp. 1) si la couleur dominante est sur le marquage 0 (resp. 1)
y_i = 0 (resp. 1,-1) si la couleur dominante est sur le marquage 0 (resp. 1,-1)


(ii) M = < H;B,A,P,G,D > ; M = l'ensemble des formules
(M, .) où la loi '.' : concaténation V,T ==> VT

(iii) Action '•' de M sur G⁺ :
G⁺ x M --> G⁺
(s,V) --> s•V = t
On impose à '•' les 4 axiomes suivants:
A₁. s•I = s ;
A₂. (s•V)•T = s•(VT)
A₃. a donné,fixé
a•V = a ==> V=I ; seul I possède des points fixes.
A₄. s•(VT) = (s•V)(s•T)

(iv) Définition un état :
G = {s∈G⁺ | e•V=s , V∈M} , e=état résolu
G = l'ensemble des états, ce sont des configurations provenant de M

(v) Théorème fondamental de la Cubologie
Quelles sont les conditions nécessaires et suffisantes pour qu'une configuration soit un état ?
On pose :
s=(u,x,v,y)∈G⁺
(F) : x=0 (mod 2)
(T) : y=0 (mod 3)
(P) : sig(u) = sig(v)
théorème :
G = {s∈G⁺ , s vérifie (F), (T), (P)}

Formule, Etat

Il y a une bijection entre M et G , voyons ...
Soit
f: M --> G
V --> f(V) = e•V = s
Le but est donc de montrer que f est bijective.

1. f est injective
f(V) = f(T)
e•V = e•T
(e•V)•T' = (e•T)•T'
e•(VT') = e•(TT') ; Axiome2
e•(VT') = e•I = e ; Axiome1
VT' = I ; Axiome3
d'où
V = T

f est donc injective , en fait f est injective par définition même

2. f est surjective
On prend donc un élément s de G , et il faut trouver une formule dont il provient
s=(u,x,v,y)∈G et on a:
(F) x = 0 (mod 2)
(T) y = 0 (mod 3)
(P) sig(u) = sig(v)

La preuvre est constructive, càd on construit petit à petit la formule
On va faire ça en plusieurs étapes.
On coupe (u,x,v,y) en deux morceaux (u,x,v,y) = (u,x-u(x),v,y-v(y))(id,x,id,y)

Soient les 3 formules suivantes:
F₁ = A[DH]A'H => permuter 2 arêtes
F₂ = (A[DH]A'H)² => pivoter 2 arêtes
F₃ = [DH]G'[HD]G => 3-cycle-sommets
F₄ = [DH]²G'[HD]²G => pivoter 2 sommets adjacents

¤ (u,x-u(x),v,y-v(y)) :
Placer les arêtes
On utilise F₁ (et la conjugaison) pour placer les arêtes comme exige u, c'est possible car les transpositions engendrent S₁₂
Puis on utilise F₂ (et la conjugaison) pour pivoter les arêtes comme exige x-u(x), c'est possible grâce à la loi des flips

Placer les sommets
On utilise F₃ (et la conjugaison) pour placer les sommets comme exige v, c'est possible grâce à la loi de parité .
Puis on utilise F₄ (et la conjugaison) pour pivoter les sommets comme exige y-v(y), c'est possible grâce à la loi des twists

¤ (id,x,id,y) :
Pivoter les arêtes
On utilise F₂ (et la conjugaison) pour pivoter les arêtes comme exige x, c'est possible grâce à la loi des flips

Pivoter les sommets
On utilise F₄ (et la conjugaison) pour pivoter les sommets comme exige y, c'est possible grâce à la loi des twists

Finalement on trouve une grosse grosse formule N , il suffit de prendre V = N' pour l'état s=(u,x,v,y).
s•N = e
e•V = s

f est surjective.

Finalement on a une bijection entre M et G. On peut même démontrer que M et G sont isomorphes.
une formule gènère un état et un seul, un état provient d'une formule unique .

NOTE : Parfois on écrit s = V (au lieu de s = e•V) ça signifie simplement que pour avoir l'état s on applique la formule V sur l'état résolu e

Commentaire

Il y a beaucoup de gens qui pensent qu'il existe plusieurs formules pour un état donné ...
par exemple:
(H²D²)³(B²D²)³ qui permute les arêtes: état s = (HA)<->(HP) et (HB)<->(BP)
(H²G²)³(B²G²)³ qui permute les arêtes: état s = (HA)<->(HP) et (HB)<->(BP)

Ou encore, à l'état résolu e:
A⁴ ==> état résolu e
[HD]⁶ ==> état résolu e
I ==> état résolu e

Comme on dit qu'elles sont toutes identiques, il faut alors dire: il y a une seule formule pour un état mais il y a des différentes façons d'écrire la formule.
(H²D²)³(B²D²)³ = (H²G²)³(B²G²)³
D' = D³
De même pour l'état résolu e:
il y a une seule formule pour l'état e mais il y a plusieurs l'écriture de cette formule
A⁴ = [DH]⁶ = I

C'est exactement quand vous écrivez:
* 1/2 = 0,5 = 3/6 = ...
l'inverse de 2 est unique mais il y a plusieurs l'écriture
ou encore
permutation identique id
* id = (a) = (b) = ...
la permutation identique id est unique , mais il y a plusieurs l'écriture
de même soit p un 3-cycle
* p = (a,b,c) = (b,c,a) = (c,a,b)
la permutation p est unique , mais il y a plusieurs l'écriture

Remarques

- Bien que M et G soient isomorphes mais ils sont très différents, leur rôle est différent , un éléments de M possède plusieurs l'écriture, pas pour G . M agit sur G et non à l'inverse, et M agit sur X mais pas G
- Beaucoup de gens pensent que M c'est le groupe du Rubik's Cube, c'est-à-dire l'ensemble des mouvements est le groupe du Rubik's Cube. MAIS NON !! (M,.) agit (opère) sur G, ou sur les étiquettes X={1,2,3,...,48} c'est tout !! , mais on peut dire |M| = |G|

- Beaucoup de gens pensent que la rotation A par exemple fait bouger les sommets (parce que visuellement c'est ça). MAIS NON !!! la rotation A "ordonne", à la permutation de bouger les sommets, c'est la permutation qui bouge les sommets (elle exécute l'orde de A). Mais pourquoi ça ? c'est simple c'est dans l'écriture de la permutation !!!
Nommons les sommets par exemple a, b, c quand on écrit:
p = (a,b,c) c'est bien
p(a)=b, p(b)=c et p(c)=a ==> p déplace a en b , etc ...
mais jamais
A(a)=b, A(b)=c et A(c)=a !!!
On voit donc bien que p bouge a en b - p(a)=b -

Voici ce qu'il faut retenir:
La rotation A∈M agit sur les congigurations G⁺
G = le groupe du Rubik's Cube = l'ensemble des congigurations provenant de M = l'ensemble des configurations vérifiant (F), (T), (P) (th fondamental).

Résumons :
1) Pour un état donné il y a une seule formule associée
2) Il y a plusieurs façon d'écrire une formule, une formule a plusieurs d'écritures , si c'est possible on prend une plus courte
3) Par abuse de langage , on continue à appeler les écritures "des formules" !!

Quelques états intéressants

1. Le 4Spot

Le 4Spot ω : échanger les faces (A,P) et (G,D)
Voici la formule Ω associée à l'état 4Spot ω
Ω = BP²A²BH'G²D²H' = [ha][hd] ^tH² et
ω = e•Ω
L'état 4Spot est intéressant, car il fait partie d'un état SuperLoin (antipode, longueur=26) le SuperFlip4Spot = π c'est le seul état SuperLoin qu'on connait !

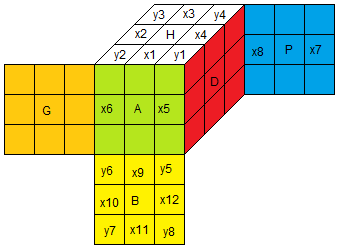
4Spot ω = e•Ω Ω = BP²A²BH'G²D²H' = [ha][hd] tH²

2. Le SuperFlip

Le SuperFlip φ : 12 arêtes retournées,
On démontre qu'il y a seulement deux états qui commutent avec tout le monde c'est e, et le SuperFlip φ :
φ s = s φ , pour tout état s
Le but est de trouver la formule associée à cet état

¤ En Jan/1995 Michael Reid a trouvé une formule de longueur 24 pour le SuperFlip, plus tard (Fev/1995) Jerry Bryan démontrait que la longueur de SuperFlip est 24, autrement dit la formule de Michael Reid est minimale.

Voici la formule Φ de SuperFlip :
Φ = D'H²PG' .AH'PBA .HB'GB² .A'DP'BA' .H'P'HB'
|Φ| = 24
φ = e•Φ
Le SuperFlip joue un rôle important, il est le seul (à part l'identité e) dans le centre de G (le groupe du Rubik's Cube).

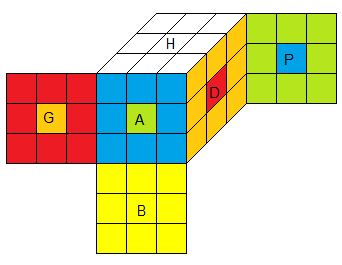
SupeFlip φ = e•Φ Φ = D'H²PG' .AH'PBA .HB'GB² .A'DP'BA' .H'P'HB'

3. Le SuperFlip4Spot

Le SuperFlip4Spot π : Il est composé du SuperFlip et du 4Spot, c'est le seul état SuperLoin (longueur=26) qu'on connait !
Voici la formule Π associée au SuperFlip4Spot
Π = H²B²G A² .H'BD² PH'B'D. GA²D HB' D'GHA'P'
π = e•Π
Michael Reid a trouvé cette formule (1998) par ordinateur
et a prouvé que c'est une des plus courte formule |Π| = 26
En Août 2014 Tomas Rokicki et Morley Davidson a démontré que le diamètre du Rubik's Cube est 26 (33 ans de galère !!!)
Donc le SuperFlip4Spot est le seul état connu qui atteint le diamètre du Rubik's Cube.

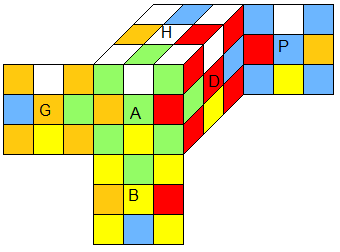
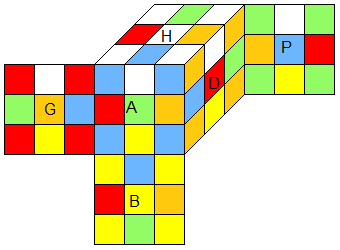SuperFlip4Spot π = e•Π Π = H²B²G A² .H'BD² PH'B'D. GA²D HB' D'GHA'P'

On a une merveilleuse formule :
π = φ ω = ω φ
Π = Φ Ω = Ω Φ

L'algorithme de résolution

Un algorithme de résolution est une suite finie d'étapes .

1. à chaque étape on peut tenir le Cube comme on veut
2. à chaque étape on peut utiliser les opérations : inverse V', puissances V^k, conjugaison XVX', rotations cube ^tZ
   Z = rotation de base {H,B,A,P,G,D}

exemple
Placer les centres : A ^tD A'
Placer les arêtes : [DH] .G'[DH]G
Pivoter les sommets : (A[DH]A'H)⁴

Posons-nous la question suivante: Combien de formules qu'utilise un algorithme ?
Donc il est raisonnable de dire que le nombre de formules qu'utilise l'algorithme c'est le nombre de formules dans l'entrée pour faire fonctionner l'algorithme.

Certaine partie de la résolution n'a pas besoin de l'algorithme , c'est intuitif et on convient de noter cette partie "0" ça signifie "pas besoin de formules, c'est intuitif"

Exemples
K = {C=[DG'], Q=[GD']}
Algo A:
-Placer les sommets : 0 , c'est intuitif, pas besoin de formules
-Placer les centres: C²
-Pivoter les sommets : C³ Q³

Algo A utilise 2 formules
Pendant l'étape par ex , "placer les centres" on peut tenir le Cube comme on veut et utiliser la conjugaison de C² càd des trucs de la forme XC²X' où X est une formule.
L'utilisation de la conjugaison est normal, car la formule C² ne déplace que certains centres précises donc à elle seule ne peut pas placer tous les centres, il faut C² et ses conjugués XC²X'.

K = {J=A[DH]A'H}
Algo B:
-Placer les arêtes: J
-Placer les sommets: J
-Pivoter les arêtes: J²
-Pivoter les sommets: J⁴
Algo B utilise 1 formule

Algo C:
-Si les arêtes sont en état impair alors H
-Placer les arêtes: P²H'G'D.P²GD'H'.P²
-Pivoter les arêtes: AH²A² .B' [H' G' ]B. A²H' A' H'
-Placer des sommets: D² .P²DAD'. P²DA' D
-Pivoter les sommets: HAB'A²H .G²H'G². AH'A²BA²
Algo C utilise 5 formules

Algo D:
K = {J=A[DH]A'H , Z=[DH]}
-Placer des arêtes; J
-Pivoter les arêtes: J²
-Placer des sommets: [ZG']=ZG'Z'G
-Pivoter les sommets: J⁴
Algo D utilise 2 formules

[1] 2 3 4 5 6 7 8

Accueil

DMJ: 15/05/2025