Indicatrice du FTO

Analyser le problème

Voyons comment on dit 2 FTO sont identiques ...

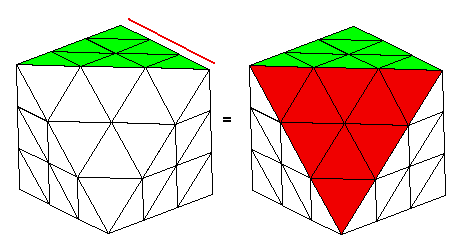Ces 2 FTO sont identiques

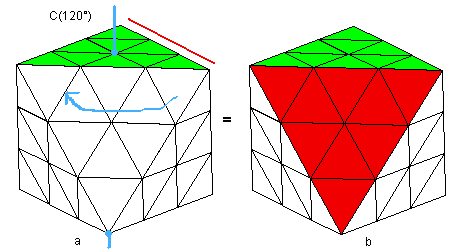On passe de a à b par la rotation C(120°)

En effet si on le tient dans la main , on ne verra pas la diférence, pour nous c'est un FTO à 3 couleurs rouge-vert et blanc. Il n'y a pas de Haut, ni de Bas, ni Gauche, ni Droite ,... c'est un FTO "mobile" on peut le bouger, tourner, pivoter .... contrairement à un FTO fixe il y a un Haut, un Bas ....

Pour un FTO mobile, on le tient dans la main comme on veut ça ne change rien, mais on passe d'une position à une autre par des rotations
Exemple on passe de fig(a) à fig(b) par la rotation C(120°)=d'axe centre-centre à 120°:

La question se pose donc quelles sont les rotations qui laissent invariant le FTO ?

Le groupe des déplacements du FTO D(O)

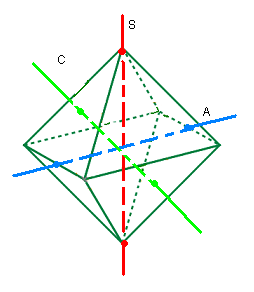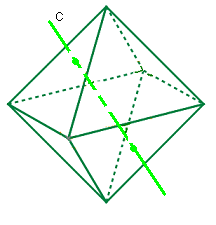3 types de rotations	Rotation C: Axe centre-centre

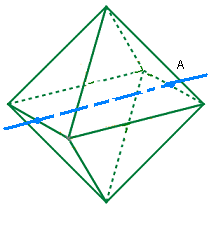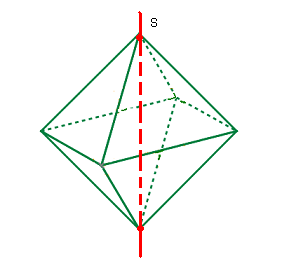
Rotation A: Axe arête-arête	Rotation S: Axe sommet-sommet

Il y a trois types de rotations sur le FTO: les rotations d'axe centre-centre, les rotations d'axe arête-arête (axe passe par les milieux d'arêtes), les rotations d'axe sommet-sommet , mais avant tout on va introduire une notation: T_kⁿ , signifie on a: n orbites à k éléments

Rotation C: Axe centre-centre
- il y a 4 (8 centres/2 = 4) rotations C(120°) ==> 2 orbites à 1 élément, 2 orbites à 3 éléments ce qui donne
4T₁²T₃²
- il y a 4 (8 centres/2 = 4) rotations C(-120°) ==> 2 orbites à 1 élément, 2 orbites à 3 éléments ce qui donne
4T₁²T₃²

Rotation A: Axe arête-arête
- il y a 6 (12 arêtes/2 = 6) rotations A(180°) ==> 4 orbites à 2 éléments ce qui donne
6T₂⁴

Rotation S: Axe sommet-sommet
- il y a 3 (6 sommets/2 = 3) rotations S(90°) ==> 2 orbites à 4 éléments ce qui donne
3T₄²
- il y a 3 (6 sommets/2 = 3) rotations S(-90°) ==> 2 orbites à 4 éléments ce qui donne
3T₄²
- il y a 3 (6 sommets/2 = 3) rotations S(180°) ==> 4 orbites à 2 éléments ce qui donne
3T₂⁴

Et bien sûr
L'identité id
- il y a un id ==> 8 orbites à 1 élément, ce qui donne
T₁⁸

Soit au total: 8+6+9+1(identité) = 24 rotations, ces rotations forment un groupe D(O) (identique à S₄ = D(O) = D(R) ) ce qu'on appelle le groupe de déplacement (isométrie positive) du FTO.
il laisse invariant le FTO.

La fonction définie par:
K = (8T₁²T₃² + 9T₂⁴ + 6T₄² + T₁⁸)/24

se nomme l'indicatrice du FTO ou l'indicateur des cycles de D(O). Pourquoi des 'cycles' ??
En fait on peut voir les choses autrement, on peut dire: Tⁿ_k , signifie on a: n cycles de longeur k
voyons pour:

Rotation A: Axe arête-arête
- il y a 6 (12 arêtes/2 = 6) rotations A(180°) ==> les faces bougent ==> quatre 2-cycles ce qui donne
6T₂⁴

L'indicatrice du FTO

On rappelle que ça vaut:

K = (8T₁²T₃² + 9T₂⁴ + 6T₄² + T₁⁸)/24

T_kⁿ , signifie on a: n orbites à k éléments
ou encore
T_kⁿ , signifie on a: n x k-cycles , n cycles de longeur k

Fonction coloriage µ, µ*

On a 2 fonctions de coloriage du FTO
La fonction µ définie par:
µ ==> dans K, on remplace T_k = c où c=le nombre de couleurs
µ = (8c²c² + 9c⁴ + 6c² + c⁸)/24
µ = (17c⁴ + 6c² + c⁸)/24

Pour simplifier on ne prend que 3 couleurs X₁, X₂, X₃
La fonction définie par:
µ* ==> Dans K , on remplace T_k = (X₁^k+X₂^k+X₃^k)

Réponse à nos questions

- Combien de FTO différents si on le peint avec seulement 3 couleurs ?
µ = (17c⁴ + 6c² + c⁸)/24
pour c=3
µ = (17.3⁴ + 6.3² + 3⁸)/24
µ = 333 !!!!

- Combien de FTO différents si on le peint avec a couleurs X₁, b couleurs X₂, et c couleurs X₃, ?
Il suffit de développer µ* et trouver le coefficient de X₁^a X₂^b X₃^c, bien sûr on ne développe pas µ* à la main il y a des programmes, des calculatrices qui le font pour nous.

Commentaire

Pour trouver l'indicatrice du FTO on est obligé de passer par le groupe de déplacement, une fois trouvé l'indicatrice K elle nous fournit 2 fonctions de coloriages µ et µ* mais seulement µ qu'on peut le calculer manuellement, quant à µ* il faut des machines pour calculer. Retenons donc simplement µ

µ = (17c⁴ + 6c² + c⁸)/24

1 2 3 [4] 5 6 7 8

Accueil

DMJ: 07/01/2024