Le groupe du Pocket

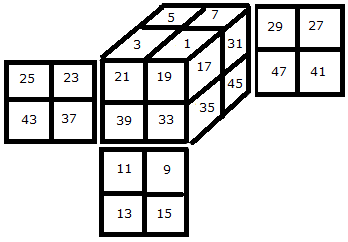
L'ensemble des autocollants X

Soit X = {1,2,3, ..., 24} l'ensemble des autocollants numérotés comme indique la fig ci-dessous . Notre but c'est de numéroter les autocollants de telle sorte qu'on puisse les regrouper facilement pour former les sommets

On utilise les nombres impairs comme le Rubik's Cube .
On commence par les facettes dominantes : 1,3,5,7, ... Puis les autres facettes dans le sens horaire.
y_i = (2i-1, 4i+13, 4i+15).

L'ensemble des étiquettes X

Soit Ψ = (HDA)⁺ la rotation étendue (on enlève le sommet, on le pivote puis on le remet !)
A chaque rotation de base {H,B,A,P,G,D} on associe une permutation {p_H, p_B, p_A, p_P, p_G, p_D} de S_x et p_Ψ la permutation étendue associée à la rotation Ψ
Soient Λ l'ensemble des permutations engendrées par {p_H, p_B, p_A, p_P, p_G, p_D}
et Λ⁺ engendrés par { p_H, p_B, p_A, p_P, p_G, p_D, p_Ψ }
Λ = < p_H, p_B, p_A, p_P, p_G, p_D > et
Λ⁺ = < p_H, p_B, p_A, p_P, p_G, p_D, p_Ψ >

Et on a :
|Λ⁺| = |G⁺|
|Λ| = |G|

Permutations standards
p_H = (1,3,5,7)(17,21,25,29)(19,23,27,31)
p_B = (9,15,13,11)(33,45,41,37)(35,47,43,39)
p_A = (1,35,11,23)(17,9,37,3)(19,33,39,21)
p_P = (7,25,13,45)(29,27,41,47)(31,5,43 ,15)
p_G = (3,39,13,27)(21,11,41,5)(23,37,43,25)
p_D = (1,29,15,33)(17,31,45,35)(19,7,47,9)

Permutations étendues
p_Ψ = (1,17,19)

et le GAP nous donne gap_pocket.txt
|Λ⁺| = |G⁺| = 264 539 520
|Λ| = |G| = 88 179 840
On retrouve bien |G| = |Λ|

Connexion entre M et G

Rappel: M = < H,B,A,P,G,D >
Le but est de montrer la propriété suivante:
Chaque formule gènère un état, chaqu'état provient d'une formule

Chaqu'état provient d'une formule
On prend donc un élément de G , et il faut trouver une formule dont il provient
(v,y)∈G avec y = 0 (mod 3)
La démonstration se fait par construction.

Le principe est suivant : on place d'abord les sommets comme exige v, ensuite on pivote les sommets comme exige y
On coupe donc (v,y) en deux morceaux (v,z)(id,y) = (v,y) où z reste à trouver.
allons-y
(v,z)(id,y) = (v,z+v(y)) d'où
z+v(y) = y ==> z = y-v(y)
finalement
(v, y-v(y))(id,y) = (v,y)

Placement
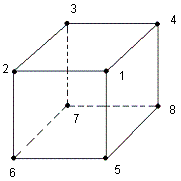
Pour faciliter l'écriture on numérote les sommets comme indique la fig1
Il faut donc trouver une formule pour placer les sommets, on prend donc la formule suivante:
Q = [DH].A'H'A
Q permute deux sommets (HDA)<->(HPD), comme S₈ est engendré par des transpositions la formule Q nous permet (avec la conjugaison) de placer les sommets comme on veut donc on peut placer les sommets comme exige v

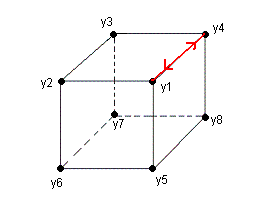fig1: Sommets numérotés	Q permute (HDA)<->(HPD)

Orientation
Il faut trouver une formule pour orienter les sommets, on prend la formule suivante:
T = [DH]²G'[HD]²G
T pivote deux sommets opposés, on peut l'utiliser pour pivoter tous les sommets grâce à la conjugaison et la loi des twists.

==> On utilise Q (et la conjugaison) pour placer les sommets comme exige v
==> On ignore l'étape y-v(y) .
==> Puis on utilise T (et la conjugaison) pour pivoter les sommets comme exige y , c'est possible grâce à la loi des twists

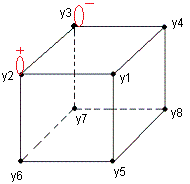fig1: Sommets numérotés	T pivote (HGP)-(HAG)+

Donc pour l'état (v,y) = (v, y-v(y))(id,y) on a bien trouvé une grosse grosse formule correspondante

Chaque formule gènère un état
On prend donc une formule S -un élément de M- , la formule gènère une configuration (w,z)∈G⁺, il faut montrer que z=0 (mod 3)
Soit n=|S|=longueur(S), on va raisonner par récurrence sur n

==> (A) Pour n=1, on prend par ex A, ce qui donne l'état (q,b) avec q=(1,5,6,2) et b=(-1,1,0,0,1,-1,0,0) on a bien b=0 (mod 3)
on fait ainsi pour toutes les autres rotations de base H,B,P,G,D, ainsi à chaque rotation de base on trouve un état (w,z) avec un vecteur d'orientation z=0 (mod 3)

(B) Supposons que la propriété soit vraie pour n (état (v,y)), montrons qu'elle reste encore vraie pour n+1 (état (v',y'))
Soit V' une formule de longueur n+1, elle est composée d'une formule V de longueur n et une rotation de base Z, elle est donc de la forme:
V' = VZ avec Z=rotation de base, et V une formule de longueur n
==> (v',y') = (v,y)(w,z)
y' = y + v(z)
comme
y=0 (mod 3) , l'hypothèse de récurrence
z=0 (mod 3) ; d'après (A) v(z)=0 (mod 3) , v ne change pas le modulo de z
d'où
y'=0 (mod 3)

Résumer: Toute formule produit un élément de G (état), tout élément de G (état) provient de M (formule)
Remarque :
1. Bien que M et G sont isomorphes, on ne peut pas identifier G = M, en effet M, ce sont des rotations, quant à G ce sont des congifurations des stickers .
2. Pour le Pocket il n'y a pas de loi de parité du genre sig(v)=1 , donc en fin de la résolution si on tombe sur une permutation de 2 sommets, on ne peut pas dire qu'on a un problème de parité, car cet état est un état légitime du twist on n'a violé aucune loi!!

1 [2]

Accueil

DMJ: 05/06/2024