Résolution du Fisher's Cube

21 Dec 2013

Méthode la croix (Jessica Fridrich) La résolution se fait exactement comme pour un Rubik's Cube, à deux exceptions près: savoir pivoter les centres, fixer les singularités.
Il y a 2 centres 'plat' (carré) on va en choisir un comme le Haut. Donc pour nous le Haut c'est le centre carré blanc

1- Notation

On va nommer les faces et les couleurs ainsi:
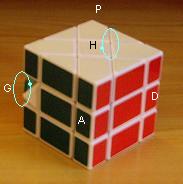
H(aut)=b(lanc) , B(as)=j(aune) , A(vant)=v(ert) , P(ostérieure)=k(lein) , G(auche)=o(range) , D(roite)=r(ouge)
d(droite-intérieur) .

Les rotations
A = tourner 90° la face Avant dans le sens des aiguilles d'une montre.
A' = tourner 90° dans le sens contraire
A² = tourner 180°
D* = tourner le bloc Droite
d = droite-intérieur (d=D*D')

Dans les dessins 3D, la face Haut a le carré blanc .
On écit (HA) pour désigner l'arête Haut-Avant ou (HDA) le sommet Haut-Droite-Avant
(HA)° = pivoter l'arête (HA)
(HDA)° = pivoter le sommet (HDA)
Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!


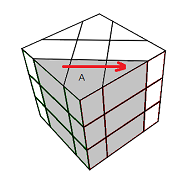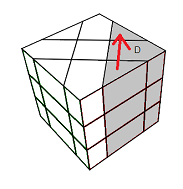Rotation A	Rotation D

A- Faire une croix

Attention:
¤ "Croix X" : Les deux couleurs latérales de l'arête doivent correspondre avec les couleurs du centre-équateur
¤ "Plus +" : Les couleurs latérales de l'arête sont sans important


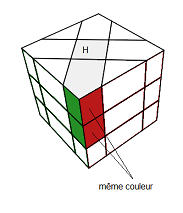Même couleurs entre l'arête et le centre

B- Placer des sommets

Aucun problème.
Placer: (BAD)->(HDA)=ABA'
Pivoter: (HDA)°=D'BDABA'

C- Faire le 2ème étage (l'équateur)

Retournez le cube (Haut -> Bas et Bas -> Haut).
Utiliser (HA)->(AD)=[HD][H'A'] ou (HD)->(AD)=[H'A'][HD] pour ranger les 4 arêtes de l'équateur.

Et voici 2 formules pour pivoter les centres:
(H)²⁺ = (HDGH²D ' G ' )²
(H)⁺(G)^- = Hd ' h ' d . H ' d ' h d
Remarque : On peut pivoter les centres à la fin, quand tout est fini.

D- Placer les sommets

D'abord on veut seulement placer les sommets, l'orientation on verra.
Echanger deux sommets
(HAG)<->(HDA)=PH' A' HP' H' AH²

On va maintenant orienter les 2 sommets-adjacents. Monter les 2 couleurs Avant vers Haut
Remarque: Si les sommets sont en opposés on remplace H' et H par H² dans la formule
(HAG)°(HDA)°= (D'BDABA') . H'(AB'A'D'B'D)H (c'est ici intervient la loi des twists)

E- Ranger les arêtes

Déplacer 3 arêtes:
(HA)->(HP)->(HD) = D². HAP'.D².PA'H.D² (c'est ici intervient la loi de patité)
Pivoter 2 arêtes:
(HA)°(HD)° = AH²A².B'[H'G']B.A²H'A'H' (c'est ici intervient la loi des flips)

F- Les états singuliers

Rappel : singularité = pseudo-parité
A cause de la symétrie (invariant par les rotations) de certaines pièces: 2 centres carrés , 4 arêtes à une seule couleur... , Le Fisher's Cube gènère 2 singularités.

1. Pivoter une arête.
Tenez le cube comme indique la fig, et appliquez la formule.
Pivoter 2 arêtes: (HA)°(HD)° = AH²A² .B'H'G'HG B .A²H'A'H'


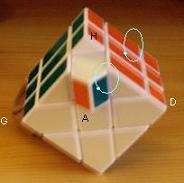l'arête à pivoter	AH²A² .B'[H'G']B .A²H'A'H'

2. Pivoter un centre à 90°.
Tenez le cube comme indique la fig, et appliquez la formule.
(H)⁺(G)^- = Hd'h'd .H'd'hd


sommet à pivoter 90°	(H)⁺(G)^- = Hd'h'd .H'd'hd

Explication sur les états singuliers
Comme il y a des pièces symétriques (ça change rien si on les pivote) comme les 2 centres carrés ou les 4 arêtes de l'équateur. Lorsqu'on mélange le cube on les pivote avec autres centres ou autre d'arêtes ce qui fait qu'on ne voit qu'une seule pièce qui change. D'où la singularité. Donc pour pivoter une arête il suffit de la pivoter avec une autre arête invariante par rotation, dans la formule
(HA)°(HD)° = AH²A² .B'H'G'HG B .A²H'A'H'
il suffit de prendre (HA)=l'arête à pivoter et (HD) l'une des arêtes de l'équateur (invariant par rotation) , et le tour est joué !
même chose pour pivoter un centre à 90°
(H)⁺(G)^- = Hd'h'd .H'd'hd
il suffit de choisir G = "le centre à pivoter" et H un centre carré (invariant par rotation) .