Résolution du Pyraminx
11
Dec
2012
Méthode les centres d'adord
Bien que le Pyraminx est un twist assez simple, mais il est vraiment intéressant du point de vu résolution et théorique.
En effet il constitue la premiere famille de base parmi les familles de twist: Rubik's Cube, Skewb, Square-1 ....
 |
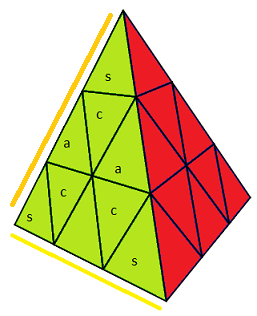 |
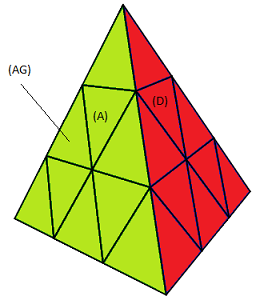
| (A)=face Avant |
s=sommet, c=centre, a=arête |
1- Notation
Les faces seront notées entre parenthèses: (A)=face Avant, (G)=face Gauche, (D)=face Droite, (B)=face Bas
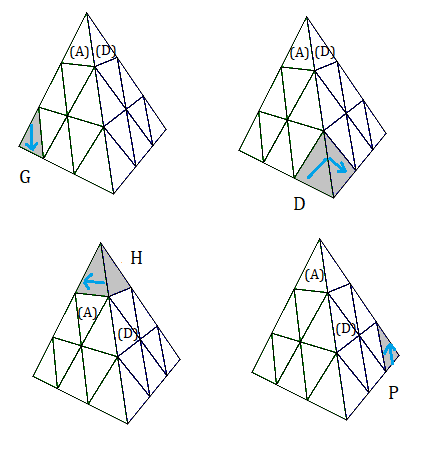
Rotations sommets
Les sommets seront notés sans parenthèses: (BGA)=G, sommet G (rotation G)
Voici les rotations (par rapport aux sommets) utilisées:
G(auche), D(roite), H(aut), P(ostérieur).
(BGA) = G, (BAD) = D, (AGD) = H, (BDG) = P
G = tourner 120° dans le sens des aiguilles d'une montre.
G' = tourner 120° dans le sens contraire (-120°)
G² = tourner 240°
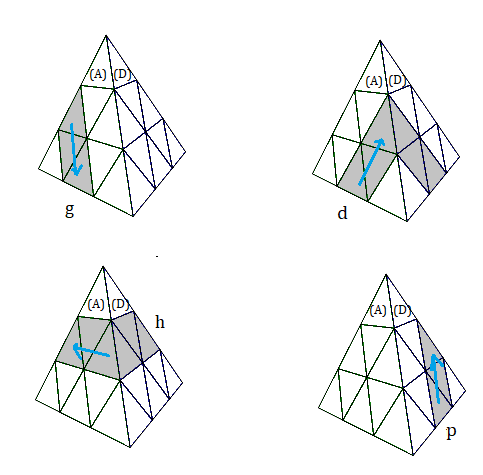
Rotations tranches
g = tourner 120° dans le sens des aiguilles d'une montre.
g' = tourner 120° dans le sens contraire (-120°)
g² = tourner 240°
 |
|
| Rotations sommets |
|
 |
|
| Rotations tranches |
|
Dans les dessins, la face (A) porte la couleur
vert, et on voit le (B)as (
jaune) .
On écit (AG) pour désigner l' arête Avant-Gauche
(AG)° = pivoter l' arête (AG)
Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!
On va choisir la face (B)as
jaune et (A)vant
vert une fois pour tout.
A- Former les centres
1.
Placer les centres
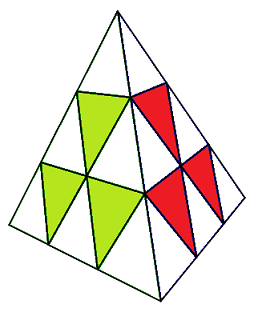
On regroupe les centres face par face, en Logo "Danger Nucléaire" comme indique la fig1 ci-dessous.
On commence par placer les centres verts comme la fig2 et faites: g'd
 |
 |
| fig1: Ce qu'on veut |
fig2: g'd |
Une fois finir les centres (A)vant , on tourne p (si nécessaire) pour finir les centres des autres faces.
2.
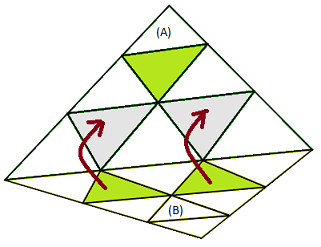
Placer les sommets
On tourne simplement les sommets pour avoir la même couleur avec les centres ! c'est tout !
 |
|
| Placer les sommets |
|
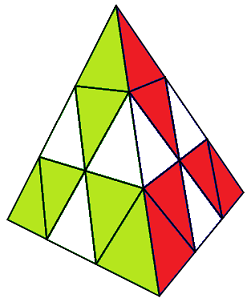
B- Placer les arêtes
On finit d'abord le Bas avec le crochet [gd']=gd'g'd
(AG)->(BA)->(AD) = [gd']
Puis le 1er étage par : (AG)->(AD)->(GD) = dhd'hdhd'
 |
 |
| [gd']=gd'g'd |
(AG)->(AD)->(GD) = dhd'hdhd' |
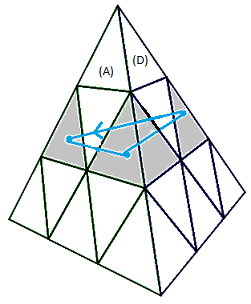
C- Orienter les arêtes
On oriente les arêts avec la formule ci-dessous.
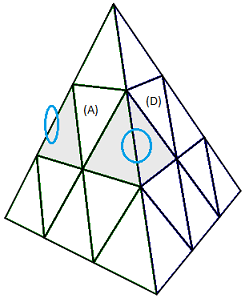
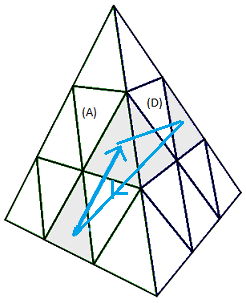
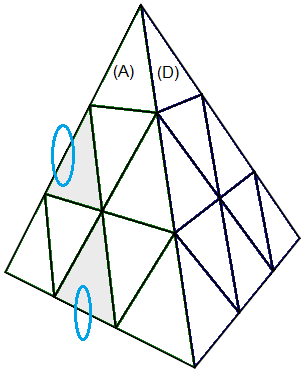
Orienter 2 arêtes: (AG)°(AD)° = [gd'][h'd]
 |
 |
| (AG)°(AD)° = [gd'][h'd] |
Et Hup là |
Résumé :
I. La résolution du Pyraminx est très simple, on n'utilise que 3 formules:
- Permuter 3 arêtes: (AG)->(BA)->(AD) = [gd']
- Permuter 3 arêtes-Haut:(AG)->(AD)->(GD) = dhd'hdhd'
- Pivoter 2 arêtes: (AG)°(AD)° = [gd'][h'd]
II. a. Les sommets ne servent strictement à rien !!! on peut donc les supprimer ou tronquer comme dans le Tetraminx.
b. Les centres ne servent pas grande chose non plus !!! car ils tournent autour de leur sommet c'est tout. Un centre Haut tourne autour du sommet Haut mais
ne prend jamais la place d'un centre Gauche par exp. Dans le Pyraminx les seules pièces intéressantes ce sont des arêtes, et le vrai nombre permutations est donc 6!2
6/2x2 = 11520
Bien que simple mais le Pyraminx possède quand même 2 lois vraiment intéressantes:
1. Conservation des flips.
2. Permutation pair.
Formules suplementaires
Voici quelques formules intéressantes
 |
 |
| (BA)->(AD)->(GD) = [dh] |
(AG)°(BA)° = [dh'][g'h] |
 |
|
| (hd'g)3 = SuperFlip |
|
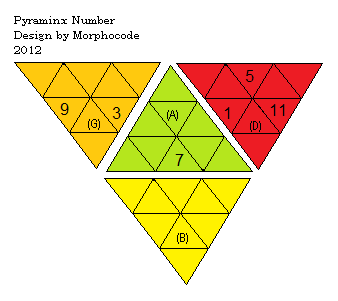
Pyraminx number
Voici un motif qui rend la loi
conservation des flips visible sur votre Pyraminx.
Si vous n'avez pas de chiffres vous pouvez les remplacer par les stickers ronds (3x3x3) de CUBESMITH.
 |
|
| Pyraminx number |
|
Sommer les faces de façon suivante:
(A)=(AD)+(AG)
(D)=(GD)+(BD)
(B)=(BA)+(BG)
Le total doit être un nombre pair: (A)+(D)+(B)= n, n est toujours pair !!!
 |
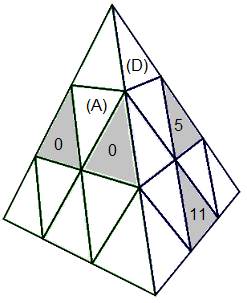 |
| (A)+(D)+(B)= n, n est toujours pair |
(A)+(D)+(B)= 0+16+0 |
Si vous avez mis les stickers ronds à la place des chiffres alors le total des ronds de ces 3 faces est toujours un nombre pair.
1 [2]
Accueil
DMJ: 09/10/2024



















