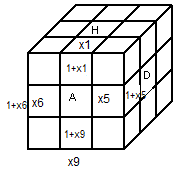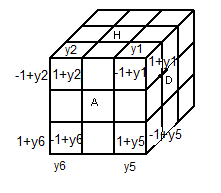La face cachée du Rubik's Cube

La parité, la signature

Commençons par voir ce que c'est un k-cycle (k ≥ 1): un k-cycle c'est un déplacement de k objets en cycle.
p = a->b = (a,b) = a<->b un 2-cycle (permuter a,b ; échanger a,b ; transposer a,b ....) longueur = 2 (nombre de lettres) . On dit aussi une transposition (a,b)
p = a->b->c = (a,b,c) un 3-cycle, longueur = 3 qui vaut aussi: (a,b,c)=(a,b)(a,c) ^(°)
Attention !! quand on applique x on applique à gauche : x.(a,b)(a,c)
p = a->a = (a) = id=identité = 1-cycle , longueur = 1

On définit la signature d'un k-cycle par:
Si (k-1) est pair, la signature de ce k-cycle est pair , impair sinon
par ex
sig(4-cycle) = 4-1 = 3 = impair.
sig(3-cycle) = 3-1 = 2 = pair.
sig(2-cycle) = 2-1 = 1 = impair.
sig(1-cycle) = sig(id) = 1-1 = 0 = pair.
etc ....
Il est plus commode pour les calculs de poser pair=1 et impair=-1 on a donc
sig(k-cycle) = (-1)^k-1

Il y a une autre façon de voir la signature. Soit p une permutation composée de n couples (a,b): si n est pair on dit que la permutation p est pair, impair sinon
par ex: p =(a,b)(a,d)(c,e) => 3 couples => sig(p)=impair=-1
p = (a,b)(c,d) => 2 couples => sig(p)=pair=1
donc
sig(p) = (-1)ⁿ ; n = le nombre de couples à permuter

On a les propriétés suivantes:
I. sig(pq) = sig(p).sig(q)
II. On démontre que: toute permutation est décomposée en cycles disjoints (pas de lettre un commun)
ex: (a,b,c)(d,e)(f,g,h) disjoints
(a,c,b)(c,d) non-disjoints
III. On démontre que: toute permutation est décomposée en couples (pas forcement disjoints)
ex: (a,b,c,d)=(a,b)(a,c)(a,d) ;distibutive
(a,b,c) = (a,b)(a,c) ;distributive

NOTE:
Par exemple dans S₈
Une permutation sera notée q=[2,3,1,4,7,6,8,5] (avec "[", "]") ça signifie: q(1)=2, q(2)=3, q(3)=1, q(4)=4, q(5)=7, q(6)=6, q(7)=8, q(8)=5, il y a toujours 8 nombres
tandis que p=(3,7,2,6) (noté avec "(", ")" ) est un cycle et on a: p(3)=7, p(7)=2, p(2)=6, et p(6)=3, p(1)=1, p(4)=4, p(5)=5, p(8)=8.
en passant par la notation "permutation" on a
p=[1,6,7,4,5,3,7,8]
Il y a donc une différence entre [2,3,1,4,7,6,8,5] et (2,3,1,4,7,6,8,5)

(°)ATTENTION:
==> On a : pq ≠ poq (en fait pq = qop) ; on lit de gauche à droite
==> f(x) = x.f (lire f appliquer à x) ; on lit de gauche à droite

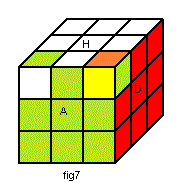
Orientation des sommets

1) Le marquage

Poser votre Rubik's Cube sur une table de telle sorte qu'une de ses faces soit en face de vous, on fixe ainsi le Cube ou on oriente le Cube. Le Cube possède alors 6 faces nommées ainsi:
H(aut), B(as), A(vant), P(ostérieur), G(auche), D(roite).

La couleur des faces dépend des Cubes achetés, des propriétaires !! car on peut changer les stickers à notre grés !. Pour nous la couleur standard des faces sont:
H(aut)=b(lanc), B(as)=j(aune), A(vant)=v(ert), P(ostérieur)=k(lein), G(auche)=o(range) et D(roite)=r(ouge)

Chaqu' emplacements-sommets a 3 facettes marquées 0, 1, -1
Nous décidons de marquer notre Cube de façon suivant: 0 sur le Haut et le Bas puis dans le sens horaire 1, -1. C'est le marquage usuel.

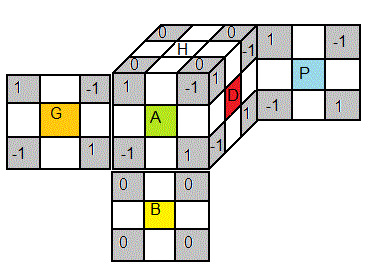Table des marquages des sommets (0=bien orienté)

Ce qui donne les faces dominantes: H > B (les faces marquées zéro 0)

2) Le nom des emplacements-sommets

Le nom de l'emplacement-sommet compose par ces trois faces écrit entre parenthèses par ex (ABD)
Lorsqu'on écrit un emplacement-sommet, on a 6 écritures :
(ABD) = (ADB) = (DAB) = (DBA) = (BAD) = (BDA)
Il faut sélectionner une seule, pour ça on utilise la règle suivante:

Règle des noms des emplacements: face dominante + sens horaire

Voici donc les 8 noms des emplacement-sommets.

(HDA), (HAG), (HGP), (HPD)
(BAD), (BGA), (BPG), (BDP)

3) La couleur dominante

Pour un sommet, quelle est sa couleur dominate ? et pourquoi ?
Pour savoir la couleur dominante d'un sommet c'est très simple une fois le marquage est donné. A l'état résolu, la couleur dominante c'est la couleur qui est sur zéro 0. Parce que à l'état résolu tous les sommets sont en bonne orientation

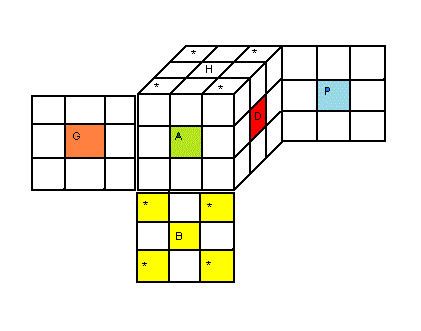* = les couleurs dominantes (* placé sur 0)

D'où les couleurs dominantes: blanc > jaune (couleur marquées zéro 0)

4) Le nom des sommets

Le nom du sommet compose par ces trois couleurs écrit entre parenthèses par ex (vjr)

Lorsqu'on écrit un sommet, on a 6 écritures :
(vjr) = (vrj) = (rvj) = (rjv) = (jvr) = (jrv)
Il faut sélectionner une seule, pour ça on suit la règle suivante:

Règle des noms des pièces: couleur dominante + sens horaire

Voici les noms des 8 sommets.

(brv), (bvo), (bok), (bkr)
(jvr), (jov), (jko), (jrk)

5) Numérotation des sommets

On va numéroter les sommets comme indique la fig ci-dessous
y₁=(brv), y₂=(bvo), y₃=(bok), ...
Remarque : on a placé y_i sur la facette marquée 0

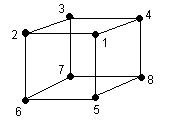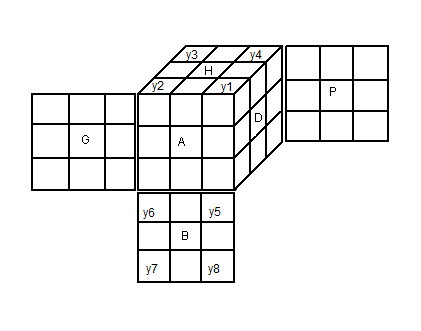Table des numérotations simples des sommets	Table des numérotations des sommets: yi

y₁=(brv), y₂=(bvo), y₃=(bok), y₄=(bkr),
y₅=(jvr), y₆=(jov), y₇=(jko), y₈=(jrk).

Au départ les emplacements contiennent les y_i comme suite:
(HDA)=y₁, (HAG)=y₂, (HGP)=y₃, (HPD)=y₄
(BAD)=y₅, (BGA)=y₆, (BPG)=y₇, (BDP)=y₈

Les sommets y_i se baladent pour se placer dans les emplacements-sommets, à chaque fois que la couleur dominante se trouve sur la facette marquée 1 son orientation vaut 1 (1 twist) , sur -1 son orientation vaut -1 (-1 twist) , sur 0 son orientation vaut zéro (0 twist, 0=bien orienté). Par exemple, le sommet y₆=(jov) se place en (HDA) avec jaune=A, alors y₆ vaut -1 (-1 twist) car la couleur dominante jaune est sur la facette -1, de même pour le sommet y₁=(brv) dans (HAG) avec blanc=A, alors y₁=1 (1 twist) car la couleur dominante blanc se trouve sur 1 .

6) L'arbre de marquage des emplacements-sommets

I. On a 2 types de marquages: horaire et anti-horaire
==> Horaire : on place 0 sur une facette puis 1,-1 dans le sens horaire ceci fait pour tous les 8 sommets
==> Anti-Horaire : on place 0 sur une facette puis 1,-1 dans le sens anti-horaire ceci fait pour tous les 8 sommets
Ces marquages sont tous équivalents (dans le sens où ils donnent les même lois du Rubik's Cube) , pour voir , il suffit de dessiner les arbres de marquages.

II. Lorsqu'on fait une rotation de base, il n'y a que 4 sommets disons a->b->c->d qui se déplacent, donc chaqu' arbre a 4 niveaux.

III. Chaque emplacement-sommet a 3 possibilités et on a 4 niveaux, l'arbre a 3⁴ = 81 branches

REMARQUE : on peut marquer "-1" = "2" = "-" et "1" = "+1" = "+" , c'est pareil.

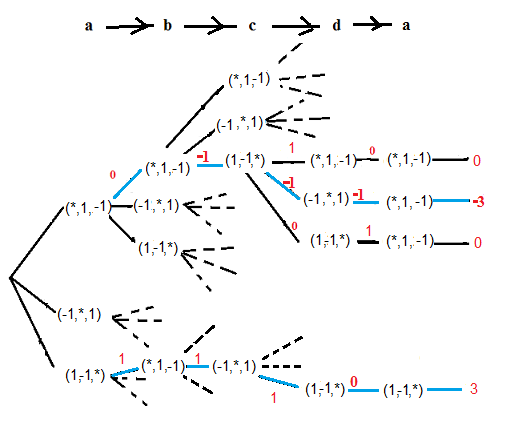
On va simplement dessiner une partie de l'arbre horaire.

* = les couleurs dominantes (* placé sur 0)

Voyons sur un chemin de l'arbre
a=(*,1,-1) -> b=(*,1,-1) -> c=(1,-1,*) -> d=(-1,*,1) -> a=(*,1,-1) => orientation = -3
on passe de a->b la couleur dominante '*' est sur 0
on passe de b->c la couleur dominante '*' est sur -1
on passe de c->d la couleur dominante '*' est sur -1
on passe de d->a la couleur dominante '*' est sur -1
total = -3

a=(1,-1,*) -> b=(*,1,-1) -> c=(-1,*,1) -> d=(1,-1,*) -> a=(1,-1,*) => orientation = 3
on passe de a->b la couleur dominante '*' est sur 1
on passe de b->c la couleur dominante '*' est sur 1
on passe de c->d la couleur dominante '*' est sur 1
on passe de d->a la couleur dominante '*' est sur 0
total = 3
etc ...

Il n'est pas difficile de calculer le nombre total des marquages possibles n. En effet un arbre a 81 branches, une branche représente le marquage de 4 emplacements-sommets comme on a 8 emplacements-sommets il nous faut 2 branches, càd il faut choisir 2 branches parmi 81, et on a 2 arbres donc
n = 2 x (⁸¹ ₂) = 81 x 80 = 6480

L'arbre de marquage des emplacements-sommets nous montre qu'une rotation de base, apporte 0 ou 3 ou -3 au nombre de twits

Orientation des arêtes

Comme pour les sommets, on a d'une part les emplacements-arêtes à 2 facettes marquées 0, 1 et d'autre part les arêtes ayant 2 couleurs dont l'une est dominante. Lorsqu'une arête se loge dans un emplacement-arête et que sa couleur dominante est sur la facette marquée 1 on dit que l'orientation de ce sommet vaut 1, de même, sur 0 son orientation vaut 0 dans ce cas on dit que le sommet est bien orienté.

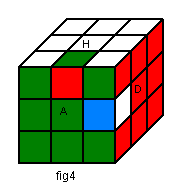
1) Le marquage

Le marquage des facettes est 0, ou 1, car les arêtes n'ont que 2 possibilités pour pivoter
Nous décidons de marquer notre Cube comme indique la fig ci-dessous: 0 sur H, B puis 0 sur A et P. C'est la marquage naturel
ce qui donne l'ordre de faces:
H > B > A > P > G > D (les faces marquées zéro 0)

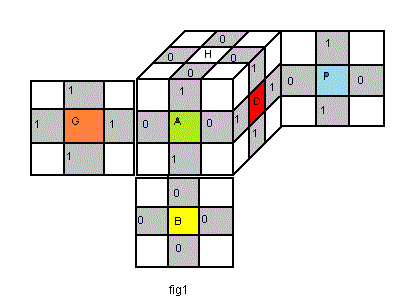Tabledes marquages des arêtes (0=bien orienté)

2) Le nom des emplacements-arêtes

Le nom de l'emplacement-arête compose par ces deux faces écrit entre parenthèses par ex (AB)

Lorsqu'on écrit l'emplacement (AB) , on a deux écritures
(AB) = (BA)
Il faut choisir une seule, suivante la règle "face dominante + sens horaire" , ici on n'a pas besoin "sens horaire" donc les 12 noms emplacements-arêtes sont:

(HA), (HG), (HP), (HD)
(AD), (AG), (PG), (PD)
(BA), (BG), (BP), (BD)

3) La couleur dominante

Pour une arête, quelle est sa couleur dominate ? et pourquoi ?
Une fois le marquage est donné, à l'état résolu, la couleur dominante c'est la couleur qui est sur zéro 0. Parce que à l'état résolu tous les arêtes sont en bonne orientation

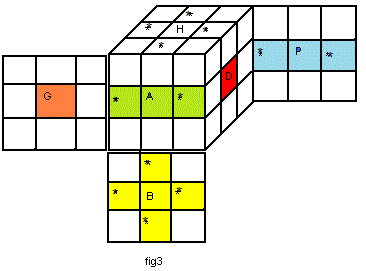* = les couleurs dominantes (* placé sur 0)

Donc les couleurs dominantes sont : blanc > jaune > vert > klein > orange > rouge (les couleurs marquées zéro 0) .

4) Le nom des arêtes

Le nom de l'arête compose par ces deux couleurs écrit entre parenthèses par ex (vj)

Lorsqu'on écrit l'emplacement (vj) , on a deux écritures
(vj) = (jv)
Il faut choisir une seule, suivante la règle "couleur dominante + sens horaire" , ici on n'a pas besoin "sens horaire" donc les 12 noms arêtes sont:

(bv), (bo), (bk), (br)
(vr), (vo), (ko), (kr)
(jv), (jo), (jk), (jr)

5) Numérotation des arêtes

On va numéroter les arêtes comme indique la fig ci-dessous
x₁=(bv), x₂=(bo), x₃=(bk), ....
Remarque : on a placé x_i sur la facette marquée 0

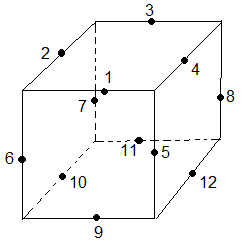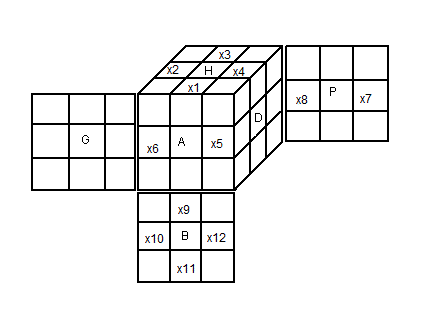Table des numérotations simple des arêtes	Table des numérotations des arêtes: xi

voici les 12 arêtes numérotées x_i :

x₁=(bv), x₂=(bo), x₃=(bk), x₄=(br),
x₅=(vr), x₆=(vo), x₇=(ko), x₈=(kr),
x₉=(jv), x₁₀=(jo), x₁₁=(jk), x₁₂=(jr).

Au départ les emplacements contiennent les x_i comme suite:
(HA)=x₁, (HG)=x₂, (HP)=x₃, (HD)=x₄
(AD)=x₅, (AG)=x₆, (PG)=x₇, (PD)=x₈
(BA)=x₉, (BG)=x₁₀, (BP)=x₁₁, (BD)=x₁₂

Les arêtes x_i se baladent d' emplacement en emplacement pour se loger dans des emplacements-arêtes (HA), (HD)..., à chaque fois que la couleur dominante se place sur la facette marquée 1 sa orientation vaut 1 (1 flip), sinon elle vaut zéro (0=bien orienté), Par exemple l'arête (vr)=x₅ se place en (HA) avec vert=H, alors x₅ vaut 0 (0 flip, bien orienté) car la couleur dominante vert est sur la facette marquée 0, De même, l'arête (bk)=x₃ est dans (AD) avec blanc=D, alors x₃ = 1 (1 flip) car la couleur dominante blanc se trouve sur 1

6) L'arbre de marquage des emplacements-arêtes

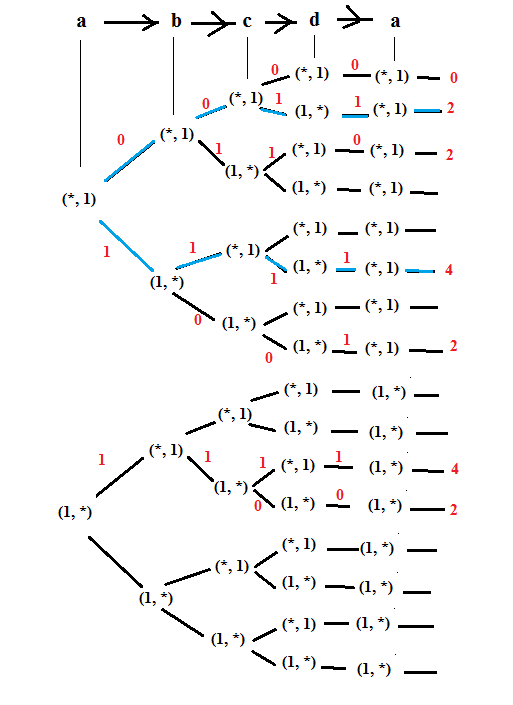
Il y a plusieur marquages possibles mais ils sont tous équivalants (dans le sens qu'ils donnent les même lois du Rubik's Cube) pour voir dessinons l'arbre de marquage des emplacements-arêtes. Lorsqu'on fait une rotation de base, il n'y a que 4 arêtes disons a->b->c->d qui se déplacent, l'arbre a donc 4 niveaux. comme chaque emplacement-arête a 2 possibilités et on a 4 niveaux donc l'arbre a 2⁴ = 16 branches.

* = les couleurs dominantes (* placé sur 0)

Voyons sur un chemin de l'arbre
a=(*,1) -> b=(*,1) -> c=(*,1) -> d=(1,*) -> a=(*,1) => orientation = 2
on passe de a->b la couleur dominante '*' est sur 0
on passe de b->c la couleur dominante '*' est sur 0
on passe de c->d la couleur dominante '*' est sur 1
on passe de d->a la couleur dominante '*' est sur 1
total = 2

a=(*,1) -> b=(1,*) -> c=(*,1) -> d=(1,*) -> a=(*,1) => orientation = 4
on passe de a->b la couleur dominante '*' est sur 1
on passe de b->c la couleur dominante '*' est sur 1
on passe de c->d la couleur dominante '*' est sur 1
on passe de d->a la couleur dominante '*' est sur 1
total = 4
etc ...

De même on va calculer le nombre total des marquages possibles n. l'arbre a 16 branches, il faut choisir 3 branches (3x4=12 arêtes) parmi 16
n = (¹⁶ ₃) = 16x15x14/3! = 560

L'arbre de marquage nous montre qu'une rotation de base, apporte 0 ou 2 ou 4 au nombre de flips

La loi de composition de (G,.)

Comment a t-on trouvé la loi de composition '.' de G, (G,.) ? voyons voir:

I) Pour les arêtes : La rotation de base A gènère, pour les arêtes, une permutation p et une orientation a : A => (p,a).
D'après le marquage on a:
(HA)=(x₁,1+x₁), (AD)=(x₅,1+x₅), (BA)=(x₉,1+x₉), (AG)=(x₆,1+x₆+1)

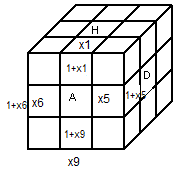Orientation des arêtes

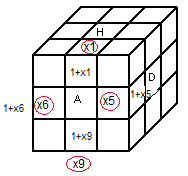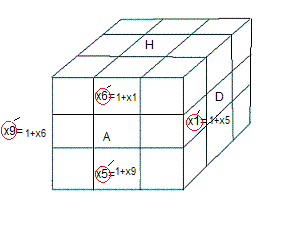Avant la rotation A	Après la rotation A

x'₁ = 1+x₅
x'₂ = x₂
x'₃ = x₃
x'₄ = x₄
x'₅ = 1+x₉
x'₆ = 1+x₁
x'₇ = x₇
x'₈ = x₈
x'₉ = 1+x₆
x'₁₀ = x₁₀
x'₁₁ = x₁₁
x'₁₂ = x₁₂

Or pour la rotation A on a:
Permutation: p = (1,5,9,6)
Orientation: a = (1,0,0,0,1,1,0,0,1,0,0,0)
d'où:
x' = a + p(x)

Chaque formule F (état (u',x')) commence par une rotation de base par ex A (état (p,a)) et le reste T (état (u,x)) on a :
F = AT
(u',x') = (p,a)(u,x) = (pu,a+p(x))
ce qui suggère la loi dans (G, .)
(u,x)(u',x') = (uu',x+u(x'))

II) Pour les sommets : De même une rotation de base gènère, pour les sommets, une permutation et une orientation par exemple A => (q,b) , le but est de calculer q et b
D'après le marquage on a:
(HAG)=(y₂,1+y₂,-1+y₂), (HDA)=(y₁,1+y₁,-1+y₁),
(BGA)=(y₆,1+y₆,-1+y₆), (BAD)=(y₅,1+y₅,-1+y₅).

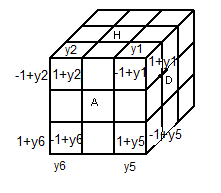Orientation des sommets

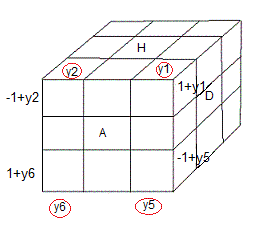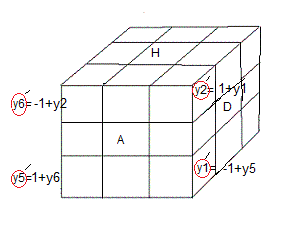Avant la rotation A	Apres la rotation A

y'₁ = -1+y₅
y'₂ = 1+y₁
y'₃ = y₃
y'₄ = y₄
y'₅ = 1+y₆
y'₆ = -1+y₂
y'₇ = y₇
y'₈ = y₈

Pour la rotation A on a:
Permutation: q = (1,5,6,2)
Orientation: b = (-1,1,0,0,1,-1,0,0)

d'où:
y' = b + q(y)
Chaque formule F (état (v',y')) commence par une rotation de base par ex A (état (q,b)) et le reste T (état (v,y)) on a :
F = AT
(v',y') = (q,b)(v,y) = (qv,b+q(y))
ce qui suggère la loi dans (G, .)
(v,y)(v',y') = (vv',y+v(y'))

L'état associé aux rotations de base

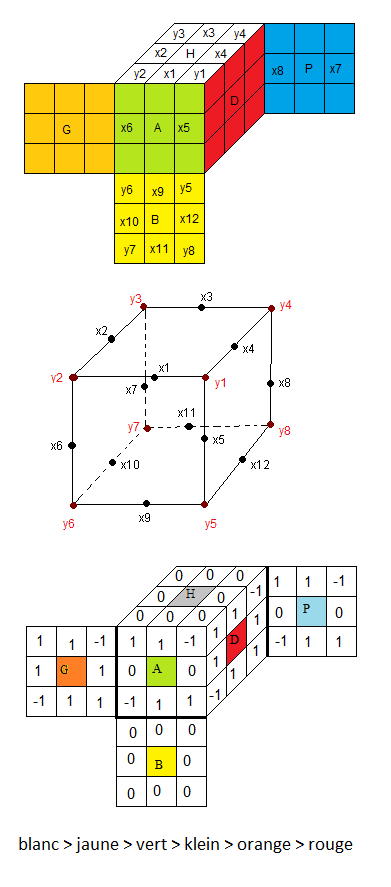Les numérotation les arêtes et les sommets xi , yi et les marquages

Pour les arêtes

H => (p,a)
p = (1,2,3,4)
a = (0,0,0,0,0,0,0,0,0,0,0,0)

B => (p,a)
p = (9,12,11,10)
a = (0,0,0,0,0,0,0,0,0,0,0,0)

A => (p,a)
p = (1,5,9,6)
a = (1,0,0,0,1,1,0,0,1,0,0,0)

P => (p,a)
p = (3,7,11,8)
a = (0,0,1,0,0,0,1,1,0,0,1,0)

G => (p,a)
p = (2,6,10,7)
a = (0,0,0,0,0,0,0,0,0,0,0,0)

D => (p,a)
p = (4,8,12,5)
a = (0,0,0,0,0,0,0,0,0,0,0,0)

Pour les sommets

H => (q,b)
q = (1,2,3,4)
b = (0,0,0,0,0,0,0,0)

B => (q,b)
q = (5,8,7,6)
b = (0,0,0,0,0,0,0,0)

A => (q,b)
q = (1,5,6,2)
b = (-1,1,0,0,1,-1,0,0)

P => (q,b)
q = (4,3,7,8)
b = (0,0,-1,1,0,0,1,-1)

G => (q,b)
q = (3,2,6,7)
b = (0,-1,1,0,0,1,-1,0)

D => (q,b)
q = (1,4,8,5)
b = (1,0,0,-1,-1,0,0,1)

Les 3 lois du Rubik's Cube

Le Rubik's Cube possède 3 lois: une sur les permutations et deux sur l'orientation.

1. Loi des flips: la somme des orientations des arêtes est un multiple de 2 (un nombre pair)

∑ x_i = 0 (mod 2) ou en abrégé x = 0 (mod 2) avec x = (x₁,x₂,x₃,...,x₁₂)
on dit qu'il y a une conservation des flips .

Démonstration :
On passe d'un état-arête (u,x) à l'autre (u',x') par une rotation de base X => (p,a)
On a
(u',x') = (u,x)(p,a)
D'où
x' = x + u(a)
d'autre part on a aussi
u(a) = 0 (mod 2)
car une rotation de base apporte un nombre d'orientations a = 0,2,4 (voir l'arbre de marquage) => a = 0 (mod 2) et que la permutation u ne change rien sur le modulo.
Donc si
x = 0 (mod 2)
on a aussi
x' = 0 (mod 2).

comme au départ, à l'état resolu l'orientation des arêtes vaut 0 (x=0 (mod 2) ), donc quelque soit l'état du Cube l'orientation des arêtes est toujours un multiple de 2.

la 1er loi est ainsi démontrée.

2. Loi des twists : la somme des orientations des sommets est un multiple de 3

∑ y_i = 0 (mod 3) ou en abrégé y = 0 (mod 3) avec y = (y₁,y₂,y₃,...,y₈)
on dit qu'il y a une conservation des twists .

Démonstration :
La démontration est assez simple. On passe d'un état-sommet (v,y) à l'autre (v',y') par une rotation de base X => (q,b)
On a
(v',y') = (v,y)(q,b)
D'où
y' = y + v(b)
d'autre part on a aussi
v(b) = 0 (mod 3)
car une rotation de base apporte un nombre d'orientation b = 0,3,-3 (voir l'arbre de marquage) => b = 0 (mod 3) et que la permutation v ne change rien sur le modulo.
Donc si
y = 0 (mod 3)
on a aussi
y' = 0 (mod 3).

comme au départ, à l'état resolu l'orientation des sommets vaut 0 (y=0 (mod 3)), donc quelque soit l'état du Cube l'orientation des sommets est toujours un multiple de 3.

la 2ème loi est ainsi démontrée.

3. Loi de parité: les permutations des arêtes et des sommets ont la même signature

Remarque: Une rotation de base gènère une permutation t sur des pièces, cette permutation déplace 4 arêtes et 4 sommets en cycle . donc t=pq avec
p = permutation arêtes un 4-cycle
q = permutation sommets un 4-cycle
on a donc sig(p)=sig(q) pour une rotation de base

Démonstration :
On passe d'un état (u,x,v,y) à l'autre (u',x',v',y') par une rotation de base X => (p,a,q,b)
On a
(u',x',v',y') = (u,x,v,y)(p,a,q,b)
D'où
u' = up
v' = vq
ça donne
sig(u') = sig(u).sig(p)
sig(v') = sig(v).sig(q)
Donc si
sig(u)=sig(v) (hypothèse de récurrence)
on a aussi
sig(u')=sig(v') d'apès la remarque ci-dessus


comme au départ, à l'état resolu personne ne bouge u=id et v=id => sig(u)=sig(v), donc quelque soit l'état du Cube (u,x,v,y) on a sig(u)=sig(v).

La 3ème loi est ainsi démontrée.

4. Loi des centres : à l'état pré-résolu, la somme des degrés des centres est un multiple de 180.

Si les centres sont orientés (avec des images par ex) alors le Rubik's Cube devient un SuperRubik's Cube.

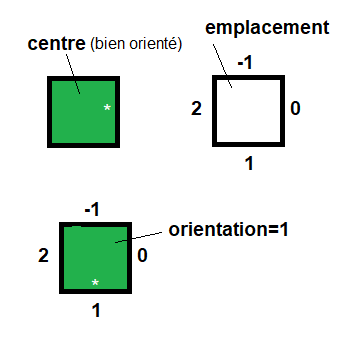l'Orientation des centres

Alors on fait come pour les arêtes, sommets
On décide arbitrairement un côté du centre est dominant, et sur l'emplacement du centre on marque (dans le sens horaire) 0 (côté dominant), 1, 2, -1
Quand le côté dominant pointe sur 0, 1, 2, -1 on dit que l'orientations de centre vaut 0 (bien orienté) 1,2,-1, ou le nombre pivot vaut 0,1,2,-1
Soit c la somme des pivots, alors par définition la direction des centres est:
dir(centres) = dir(c) = (-1)^c

On voit que
dir(centres) = sig(sommets)
Autrement dit, si la permutation des sommets est paire alors la direction des centres l'est aussi
A l'état pré-résolu (les arêtes et les sommets sont bien rangés=état résolu du Rubik's Cube), la signature des sommets est paire (sig(sommets)=1) donc la direction des centres aussi c'est-à-dire dir(centres) = (-1)^2k
c = 2k
En passant par le degré
90c = 180k
90c = le nombre de degrés des centres ,
donc à l'état pré-résolu (état résolu du Rubik's Cube) le nombre de degrés des centres est un multiple de 180.

Ceci explique pourquoi à l'état pré-résolu, on a:
¤ Des centres à 180° .
¤ Ou des couples de centres à (90°,-90°)
¤ Ou des couples de centres à (90°,90°)
¤ Ou des couples de centres à (-90°,-90°)
etc ...

exp :
(DH)¹⁰⁵ = I ==> (D)⁺ = 90° , (H)⁺ = 90°
(DH')⁶³ = I ==> (D)^- = -90° , (H)⁺ = 90°

On a 4⁶/2 = 2048 ( divisé par 2 à cause de la loi dir(c)=sig(u)=sig(v) ) de nombres de positions en plus qui faut multiplier avec le nombres d'états.

1 [2] 3 4 5 6 7 8 9

Accueil

DMJ: 04/11/2024