La face cachée du Rubik's Cube

Construction le groupe G Rubik's Cube

On ne rentre pas dans le détaille dans la contruction (action de M⁺ sur les stickers X,...) on passe directement à la phase d'analyse.

- On a 12 arêtes qui baladent partout, donc on a affaire avec S₁₂, mais les arêtes peuvent aussi se pivoter en 2 positions c'est un truc Z₂¹², pour les arêtes tout se passe dans:
S₁₂ x Z₂¹²
- On a 8 sommets qui baladent partout, donc on a affaire avec S₈, mais les sommets peuvent aussi se pivoter en 3 positions c'est un truc Z₃⁸, pour les sommets tout se passe dans:
S₈ x Z₃⁸
Finalement tout se passe dans
G⁺ = S₁₂ x Z₂¹² x S₈ x Z₃⁸ c'est l'ensemble de tous les états du cube.
G⁺ muni la loi suivante, qui lui confère un groupe, le groupe étendu du puzzle
(u,x,v,y)(u',x',v',y') = ( uu', x+u(x'), vv', y+v(y') )

et un élément de G c'est par définition:
s=(u,x,v,y)∈G⁺
u ∈S₁₂, x ∈Z₂¹², v ∈S₈, y ∈Z₃⁸
qui vérifie:
1. ∑ x_i = 0 (mod 2) en abrégeant x=0 (mod 2) avec x = (x₁,x₂,...,x₁₂)
2. ∑ y_i = 0 (mod 3) en abrégeant y=0 (mod 3) avec y = (y₁,y₂,...,y₈)
3. sig(u)=sig(v)

Il nous reste maintenant à montrer la "connexion" entre M et G, tout celà se fait en plusieurs étapes

Connexion entre M et G

Le but est de montrer la propriété suivante:
Chaque formule gènère un état, et chaqu'état provient d'une formule.

Chaqu'état provient d'une formule

On prend donc un élément de G , et il faut trouver une formule dont il provient
s=(u,x,v,y)∈G⁺ vérifiant les trois conditions (1), (2) et (3)
On va faire ça en plusieurs étapes.
La stratégie est suivante:
==> On place les arêtes
==> On oriente les arêtes
==> On place les sommets
==> On oriente les sommets

On coupe (u,x,v,y) en deux morceaux (u,x,v,y) = (u,x-u(x),v,y-v(y))(id,x,id,y)

Soient les 3 formules suivantes:
F₁ = A[DH]A'H => permuter 2 arêtes
F₂ = (A[DH]A'H)² => pivoter 2 arêtes
F₃ = [DH]G'[HD]G => un 3-cycle-sommets
F₄ = [DH]²G'[HD]²G => pivoter 2 sommets
Placer les arêtes
Avec F₁ (et la conjugaison) on peut placer toutes les arêtes comme exige u .
Une fois les arêtes sont placées on utilise F₂ (et la conjugaison) pour pivoter les arêtes comme exige x-u(x)

Placer les sommets
Les arrêtes sont bien placées, la loi de parité dit que les sommets seront placés par des permutations paires. Donc Avec F₃ (et la conjugaison) on peut placer toutes les sommets comme exige v.
Une fois les sommets sont placées on utilise F₄ (et la conjugaison) pour pivoter les sommets comme exige y-v(y)

Pivoter les arêtes
Avec F₂ (et la conjugaison) on peut pivoter toutes les arêtes comme exige x .

Pivoter les sommets
Avec F₄ (et la conjugaison) on peut pivoter toutes les sommets comme exige y .

Finalement on trouve une très grosse grosse formule pour l'état (u,x,v,y)

Chaque formule gènère un état

On prend donc une formule L -un élément de M- , la formule gènère un état (u,x,v,y)∈G⁺, il faut montrer que
1. x=0 (mod 2)
2. y=0 (mod 3)
3. sig(u)=sig(v)

(3) => Pour une rotation de base, on a sig(u).sig(v)=1 donc pour une formule on a sig(u).sig(v) x sig(u').sig(v') x sig(u").sig(v")... = 1x1x1 ... = 1

(1)+(2) => Parmi les écritures de la formule L qui donne (u,x,v,y) on prend la plus courte (c'est exactement comme 2/4, 4/8, 8/16 ... on prend le plus simple 1/2)
longueur=|L|=n, on va raisonner par récurrence sur n
Pour n=1 , on a x=0 (mod 2) et y=0 (mod 3) pour toute rotation de base {H,B,A,P,G,D}
Supposons que la propriété soit vraie pour n, montrons qu'elle reste encore vraie pour n+1
Soit Q une formule de longueur=|Q]=n+1, mais on passe de n à n+1 par une rotation de base
Q = LZ avec Z=rotation de base => (u',x',v',y') = (u,x,v,y)(p,a,q,b)
x' = x + u(a)
y' = y + v(b)
comme
x=0 (mod 2) l'hypothèse de récurrence
u(a)=0 (mod 2) la permutation u ne change pas le modulo
d'où
x'=0 (mod 2)
de même
y=0 (mod 3)
v(b)=0 (mod 3)
d'où
y'=0 (mod 3)

Résumer: Toute formule produit un élément de G (état standard), tout élément de G (état standard) provient de M
Remarque :
1. Bien que M et G soient isomorphes, on ne peut pas identifier G=M, car M et G ne jouent pas le même rôle, M agit sur G, et non à l'inverse , on fait la rotation A et on voit les étiquettes se déplacent, on ne déplace pas les étiquettes (décoller/coller) pour voir la face A tourne !!!!
2. Le Rubik's Cube est un twist enphasé.

Vérification des lois

Rappel
G⁺ = S₁₂ x Z₂¹² x S₈ x Z₃⁸ c'est l'ensemble de tous les états du cube.
et un élément de G est quelque chose comme ça:
s=(u,x,v,y)∈G⁺
u ∈S₁₂, x ∈Z₂¹², v ∈S₈, y ∈Z₃⁸
qui vérifie:
1. ∑ x_i = 0 (mod 2)
2. ∑ y_i = 0 (mod 3)
3. sig(u)=sig(v)

G⁺ = S₁₂ x Z₂¹² x S₈ x Z₃⁸ = L'ensemble de tous les états du cube, c.à.d. les états produits par tous les mouvements y compris le démontage/remontage du cube autrement dit pour n'importe quelle permutation, orientation de sommets et d'arêtes
G⁺ est le groupe étendu du Rubik's Cube
G = Le groupe du Rubik's Cube (seulement les états engendrés par les rotations {H,B,A,P,G,D} )

Vérifions ces 3 lois sur [AH]

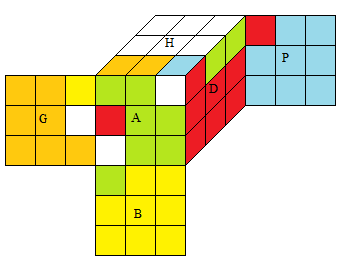[AH] = AHA'H'

Loi des flips: la somme des orientations des arêtes est pair
x₁=(bv)=0,x₄=(br)=1,x₆=(vo)=1 on a bien:
0+x₁+x₄+x₆=0 (mod 2)

Loi des twists: la somme des orientations des sommets est un multiple de 3
y₁=(brv)=0,y₄=(bkr)=-1,y₆=(jov)=-1,y₂=(bvo)=-1 on a bien:
0+y₁+y₄+y₆+y₂=0 (mod 3)

Loi de parité: les permutations des arêtes et des sommets ont la même signature
arêtes: u=1->4->6 sig(u) = (-1)^3-1 = 1
sommets: v=(1,4)(6,2) sig(v) = (-1)² = 1
d'où
sig(u)=sig(v)
c'est magique non ? !!! :-) :-)

Remarque:
Ne pas confondre un emplacement-arête avec une arête, un emplacement-arête est un objet fixe à 2 facettes, tandis qu'une arête est un objet mobile à 2 couleurs, qui se déplace d'emplacement en emplacement !! (même remarque pour les emplacement-sommets et les sommets).

1 2 [3] 4 5 6 7 8 9

Accueil

DMJ: 24/02/2022