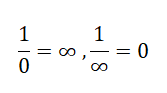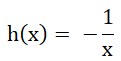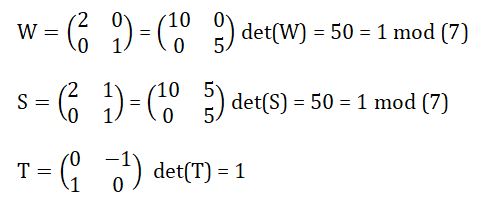La face cachée du Rubik's Cube

Groupe simple à 168 éléments : GS₁₆₈

On sait qu'il existe un seul groupe simple (non trivial=non commutatif=non Z_p) à 168 éléments. C'est le deuxième dans son genre, après le groupe alterné A₅. Le GS₁₆₈ est vraiment extraordinaire car on le trouve pratiquement partout .....

- La quartique de Klein:
E: x³y + y³z + z³x = 0 Le groupe des automorphismes qui laissent invariant E est GS₁₆₈
Aut-inv(E) = GS₁₆₈

- L'équation de degré 7:
P(x) = x⁷ - 7x + 3 = 0 Le groupe de Galois de P, est GS₁₆₈
Gal(P) = GS₁₆₈

- Dans A₇:
a=(124)(346) ; b=(17)(26)
< a,b > = GS₁₆₈

- Goupe des matrices:
GL₃ (F₂)= GS₁₆₈

- Projective:
PSL₂ (F₇)= GS₁₆₈

et ... et .... vous avez deviné ... il se trouve aussi dans le Rubik's Cube !!!!!

Considèrons le sous groupe suivant < XY^-1 > de M , engendré par les mouvements des pièces (càd on ignore les orientations) de la forme: XY^-1 avec X,Y ∈ {H,B,A,P,G,D}. Ce goupe gènère le goupe des sommets < XY^-1 >_s sous groupe de S₈, par exemple les 3 mouvements suivants BD^-1AG^-1 , AB^-1GP^-1 , HA^-1HA^-1 gènèrent 3 éléments de < XY^-1 >_s . Avec le programme GAP ( .::download GAP ici::. ), l'ordinateur calcule le cardinal de ce groupe et nous founit un joli nombre:
|< XY^-1 >_s| = 168 éléments

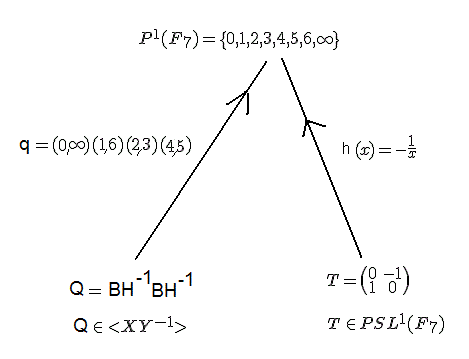
Comme dans le chapitre précédent, la droite projective de F₇ est définie par:
P¹(F₇) = { 0,1,2,3,4,5,6,∞ } en plus les opérations dans F₇ on ajoute comme d'habitude les deux opérations suivantes:

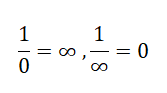
On peut dresser les tables '+' et 'X' de P¹(F₇) comme ça les opérations serons plus claires

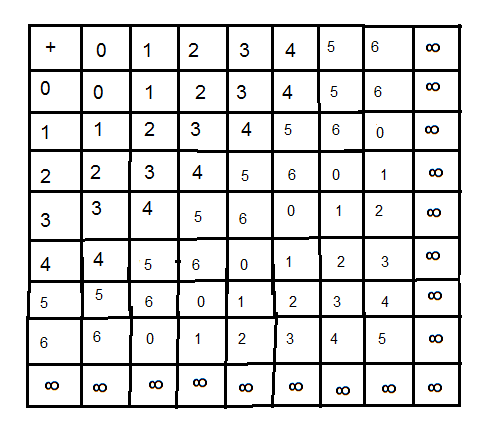addition

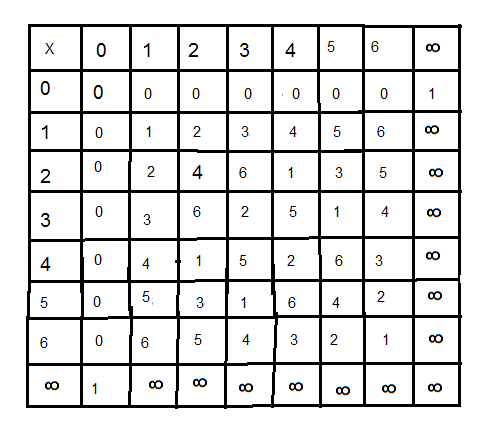multiplication

On sait que (HAG)=∞ et (HPD)=0 , plaçons maintenant les éléments de P¹(F₇) sur les sommets de Rubik's Cube de façon suivante:
A→(∞,1,3,5) et P→(0,6,2,4) permutation associées
comme la fig ci-desous

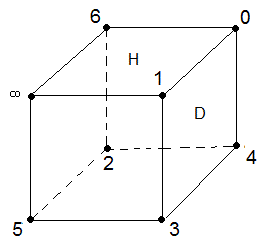
On définit ensuite 3 fonctions suivantes sur P¹(F₇)
f : P¹(F₇) → P¹(F₇)
f(x) = 2x
g : P¹(F₇) → P¹(F₇)
g(x) = 2x + 1
et
h : P¹(F₇) → P¹(F₇)

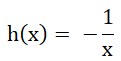
calculons les valeurs des ces fonctions (n'oubliez pas qu'on est dans P¹(F₇) )
x     = 0, 1, 2, 3 ,4, 5, 6, ∞
f(x) = 0, 2, 4, 6, 1, 3, 5, ∞

x     = 0, 1, 2, 3 ,4, 5, 6, ∞
g(x) = 1, 3, 5, 0, 2, 4, 6, ∞

x     = 0, 1, 2, 3 ,4, 5, 6, ∞
= ∞, -1, -1/2, -1/3, -1/4, -1/5, -1/6, 0
= ∞, 6, -4, -5, -2, -3, -6, 0
h(x) = ∞, 6, 3, 2, 5, 4, 1, 0

Prennons les 3 mouvements suivants:
AB^-1GA^-1 → m permutation associée
x = 0, 1, 2, 3 ,4, 5, 6, ∞
A = 0, 3, 2, 5, 4, ∞, 6, 1
AB^-1 = 0, 5, 4, 2, 3, ∞, 6, 1
AB^-1G = 0, 2, 4, 6, 3, 5, ∞, 1
AB^-1GA^-1 = 0, 2, 4, 6, 1, 3, 5, ∞ → m=(1,2,4)(3,6,5)

BD^-1 → n
x = 0, 1, 2, 3, 4, 5, 6, ∞
B = 0, 1, 5, 4, 2, 3, 6, ∞
BD^-1 = 1, 3, 5, 0, 2, 4, 6, ∞ → n=(0,1,3)(2,5,4)

BH^-1BH^-1 → q
x = 0, 1, 2, 3 ,4, 5, 6, ∞
BH^-1BH^-1 = ∞, 6, 3, 2, 5, 4, 1, 0 → q=(0,∞)(1,6)(2,3)(4,5)

m fait exactement la même chose que f(x), de même pour g(x)⇔n, h(x)⇔q

Les 3 fonctions ci-dessus fournissent les 3 matrices de déterminant=1 à coefficiences dans F₇

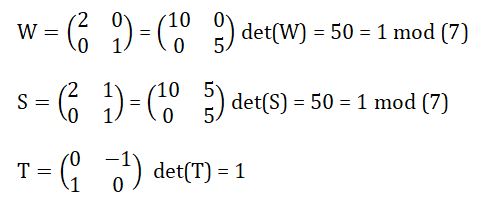
1. Formule Q ordonne à q (permutation) de bouger les éléments de P1(F7) 2. Matrice T ordonne à h(x) (fonction) de bouger les éléments de P1(F7)

On démontre que m,n,q engendrent < XY^-1 >_s et W,S,T engendrent PSL₂(F₇)
on définit maintenant la fonction z:
z : < XY^-1 >_s    →    PSL₂(F₇)
de façon suivate:
z(m)=W , z(n)=S et z(q)=T
si c'est m, je dis que ça vaut W, si c'est n, je dis que ça vaut S, ....
d'où
u=mnq → z(u)=WST

a). Montrons d'abord que c'est bien un homomorphisme
En effet un élémént de < XY^-1 >_s s'écrit comme un produit des m,n,q par exemple
v = m²qn³ et par défitition on a
z(m²qn³) = W²TS³ qui vaut
= z(m)²z(q)z(n)³ = c'est bien un homomorphisme

b). z est évidement surjectif : en effet, un élémént de PSL₂(F₇) s'écrit comme un produit des W,S,T par exemple
K = T²W²S⁴ = z(q)²z(m)²z(n)⁴ = z(q²m²n⁴)

mais |PSL₂(F₇)| = 7(7²-1)/pgcd(2,7-1) = 168
|< XY^-1 >_s| = |PSL₂(F₇)| , donc z est bijectif !!!! on a bien un bel isomorphisme entre
< XY^-1 >_s et PSL₂(F₇)

< XY^-1 >_s   =   PSL₂(F₇)   =   GS₁₆₈


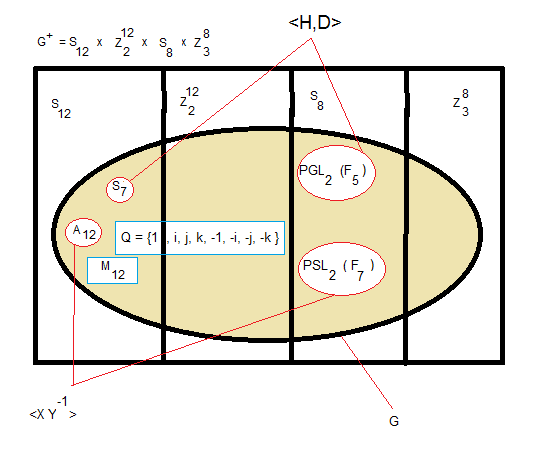
Remarque, on peut démontrer que < XY^-1 >_a   =   A₁₂

1 2 3 4 5 6 7 [8] 9

Accueil

DMJ: 30/04/2024