La face cachée du Rubik's Cube

Orbite

Si vous jouez l'Helicopter ou récemment Curvy Copter vous savez en gros ce que c'est une "orbite". Dans l'Helicopter, il y a 4 orbites pour les centres, chaqu'orbite contient 6 centres et les rotations de l'Helicopter déplacent ces centres dans leur orbite.

En Rubik's Cube vous avez aussi les orbites !! mais il est assez rare et peu d'articles en parlent sur ce sujet

Commençons par quelques observations
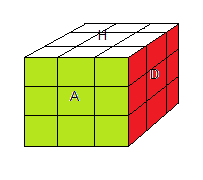
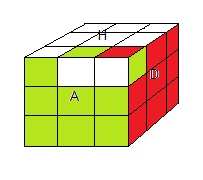
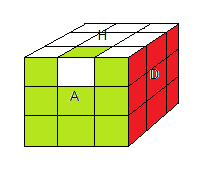
Voici deux états du Cube: l'état e₀₀₀=e (formule I) c'est l'état résolu , l'état e₁₀₀ (rotation étendue Γ) on a enlevé (HA), a pivoté puis l'a remis

Prenons l'état e₀₀₀, à partir de cette état on mélange le Cube avec les 6 rotations de base {H,B,A,P,G,D} on obtient un nouveau état disons s, l'ensemble de tous les états formés à partir de e₀₀₀, forme ce qu'on appelle orbite G₀₀₀ (il y a 43252003... états dans cette orbite)
On fait de même pour état e₁₀₀, à partir de cette état on mélange le Cube avec les 6 rotations de base {H,B,A,P,G,D} on obtient un nouveau état disons t, l'ensemble de tous les états formés à partir de e₁₀₀, forme ce qu'on appelle orbite G₁₀₀ (il y a aussi 43252003... états dans cette orbite)

l'état e000 = résolu	l'état e100

On peut toujours passer d'un état à un autre dans la même orbite, mais on ne peut pas passer 2 états dans des différentes orbites, on peut passer de s à e₀₀₀ et de t à e₁₀₀ mais pas de s à t .
Par exp l'état w est dans la orbite G₀₀₀ car on peut passer de w à e₀₀₀

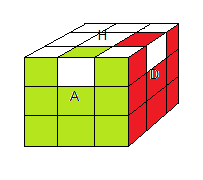l'état e000	l'état w est dans la orbite G000

La question vient naturellement à l'esprit c'est combien de orbites en a -t- on ?
La réponse se trouve dans les 3 lois fondamentales du Rubik's Cube, on sait qu'on ne peut pas passer d'une orbite à une autre comme par exp on ne peut pas passer l'état e₁₀₀ à l'état e₀₀₀, donc il suffit de violer les lois du Rubik's Cube pour trouver les orbites!!

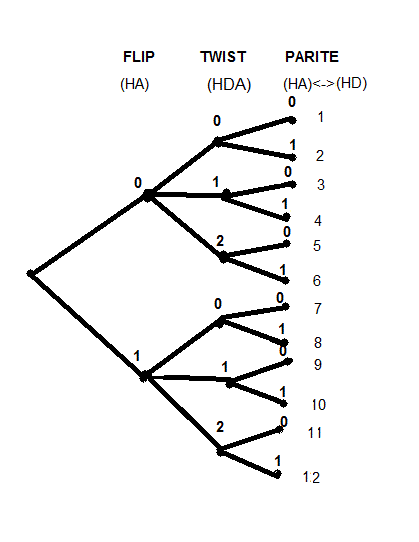
On note e_FTP l'état et G_FTP l'orbite associé ; F=Flip, T=Twist, P=Parité
e₁₁₁ signifie:
1. On enlève l'arête (HA), pivote puis la remet ; (F=1)
2. On enlève le sommet (HDA), pivote 1/3 tour dans le sens horaire puis le remet ; (T=1)
3. On enlève (HA) et (HD), permute puis les remet ; (P=1)

l'arbre des orbites

1. Violer la loi des flips: La somme des flips = 1 (mod 2)

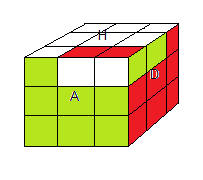
l'état e100 (rotation étendue Γ)

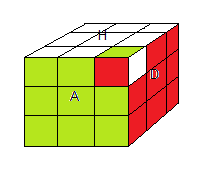
2. Violer la loi des twists: La somme des twists = 1,2 (mod 3)

l'état e010 (rotation étendue Ψ)

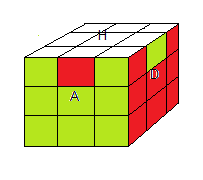
3. Violer la loi de parité: signature(sommets) ≠ signature(arêtes)

l'état e001 (rotation étendue Ω)

A partir de ces 3 états on fait des combinaisons et on trouve exactement 12 orbites pour le Rubik's Cube.

l'état e000 = résolu orbite G000	l'état e001 orbite G001

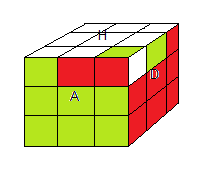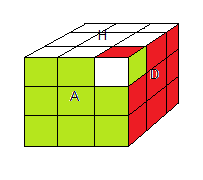
l'état e010 orbite G010	l'état e011 orbite G011

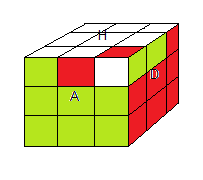l'état e020 orbite G020	l'état e021 orbite G021

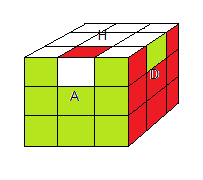l'état e100 orbite G100	l'état e101 orbite G101

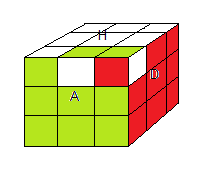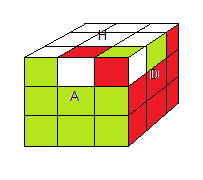l'état e110 orbite G110	l'état e111 orbite G111

l'état e120 orbite G120	l'état e121 orbite G121

Un rappel sur l'action libre et compatible d'un groupe

Une action '•' (à droite) libre et compatible est une loi externe de X x G -> X vérifiant 4 axiomes suivants:
X x G -> X
(x,g) -> x•g = x'
A₁. x•e = x (e=élémentre neutre de G)
A₂. (x•g)•h = x•(gh) ; associatif
A₃. a donné,fixé
a•g = a ==> g=e ; libre
A₄. x•(gh)=(x•g)(x•h) ; compatible

Trois définitions importantes
1. orbite : soit a∈X un élément de X
X_a = { x∈X | a•g = x où g∈G } les x qu'on peut atteindre (à partir de a) par les éléments de G, X_a ⊂ X
2. Points fixes de g : soit g∈G un élément de G
F_g = { x∈X | x•g = x} les points fixes de g , F_g ⊂ X
3. Stabilisateur : soit a∈X un élément de X
G_a = { g∈G | a•g = a} les g qui ne bougent pas a, trop "faible" pour a ;G_a=les faibles de a , G_a ⊂ G ; G_a est un sous-groupe mais pas forcement normal

Deux formules
1. |X_a| = |G\G_a| = |G|/|G_a|
2. N = 1/|G| . ∑_g |F_g|
N = le nombre d'orbites, nombre de choix, nombre de contraintes

Dans notre cas :
M⁺ agit sur G⁺ (G⁺•M⁺)

e∈G⁺ (e=résolu)
|X_e| = |G\G_e| (=nombre de classes)
G_e⁺ = { x∈G⁺ | e•V=x , V€M⁺} = G⁺
|G⁺| = |M⁺\M⁺_e| = |M⁺|/|M⁺_e|
M⁺_e = {V∈M⁺ tels que e•V = e } = {I}
|G⁺| = |M⁺|

N = 1/|G| . ∑_g |F_g|
V∈M⁺
N = 1/|M⁺| . ∑_V |F_V|
F_I = { x∈G⁺ | x•I = x} = G⁺ (tous les autres V n'ont pas de points fixes)
N = 1/|M⁺| . |G⁺|
N = 1

On peut prendre
M agit sur G (G•M)
et on trouve
|G| = |M|
N = 1

On va montrer |G⁺| = 12|G|
On va définir une relation d'équivalente suivant:
x,y ∈G⁺, x~y ⇔ ∃V∈M tel que x•V=y
'~' est visiblement une relation d'équivalente
on a 12 classes cl(r_k) k=1,2,..,12 et comme chaque classe possède le même nombre d'éléments |G| d'où
|G⁺| = 12|G|

On peut prendre
M agit sur G⁺ (G⁺•M)
V∈M
N = 1/|M| . ∑_V |F_V|
pour V=I
F_I = { x∈G⁺ | x•I = x} = G⁺ (tous les autres V n'ont pas de points fixes, V≠I, F_V=∅)
N = 1/|M| . |G⁺| = = 12|G|/|M|
N = 12

NOTE: Suivant l'action on trouve le nombre des orbites différents:
M⁺ agit sur G⁺ ⇒ 1 orbite
M agit sur G ⇒ 1 orbite
M agit sur G⁺ ⇒ 12 orbites

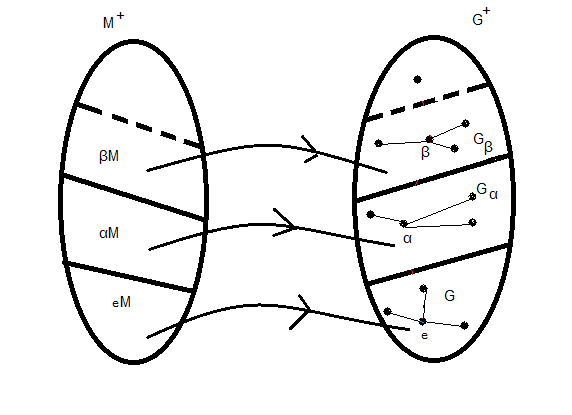G+ possède 12 orbites de la même taille (G+•M)

on a :
M⁺ = < H,B,A,P,G,D,Γ,Ψ,Ω >
M = < H,B,A,P,G,D >
|M⁺| = |G⁺|
|M⁺| = 12|M|
|M| = |G|
|G⁺| = 12|G|

1 2 3 4 5 6 7 8 [9]

Accueil

DMJ: 04/11/2024