La face cachée du Rubik's Cube

Simple rappel

On rapplle que G⁺ = S₁₂ x Z₂¹² x S₈ x Z₃⁸ est l'ensemble de tous les états du cube produits par des rotations de base {H,B,A,P,G,D} et étendues α, β, γ, δ (on démonte le Cube puis le remonte) , c'est le groupe étendu de G.

G ⊂ G⁺ avec
G = { (u,x,v,y)∈G⁺ tq ∑ x_i = 0 (mod 2), ∑ y_i = 0 (mod 3) , sig(u)=sig(v) }


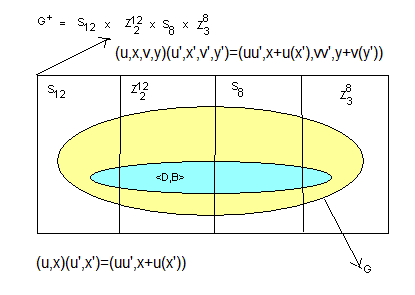
On va définir une loi de G⁺ , voici l'opération dans G⁺:

s=(u,x,v,y) et s'=(u',x',v',y')
ss' = (u,x,v,y)(u',x',v',y') = (uu',x+u(x'),vv',y+v(y')) avec u(x) = (x_u(1),x_u(2),...,x_u(12))

Le couple (u,x) ou (v,y) = (permutation,vecteur) que j'appelerai un "état" , le produit de 2 états est donc
(u,x)(u',x') = ( uu', x + u(x') )

et voilà !!!! ça a l'aire bizarre!! mais en fait c'est tout à fait logique de définir ainsi. On pense que c'est plus logique de définir la loi comme ça (u,x,v,y)(u',x',v',y')=(uu',x+x',vv',y+y') en fait non, car quand on fait une permutation u, on permute les arêtes mais on modifie aussi leur orientations !!! donc u doit intervenir dans la définition "x+x'" . Le fait de prendre u(x') parce que les lois d'orientation nous imposent voyons par ex pour A

En résumé: Un état-arête repésenté mathématiquement par (u,x) u=permutation et x=vecteur à 12 composantes à valeur {0,1} cad x=(0,0,1,0,1,0,...,1) par ex.
Le produit de 2 état-arête: (u,x)(u',x')=(uu',x+u(x')), même chose pour les état-sommet

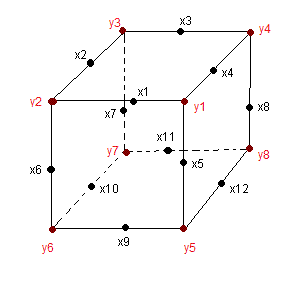
Les arêtes et les sommets sont numérotés ainsi

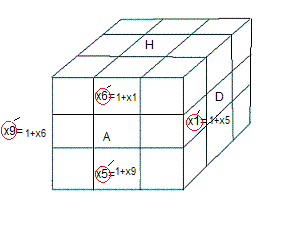
examinons les arêtes
Soit f=(p,a) l'état-arête associé de la rotation A et s=(u,x)
permutation: p = 1->5->9->6
orientation: a = (1,0,0,0,1,1,0,0,1,0,0,0)
s'=fs
(u',x')=(p,a)(u,x)
fs = (p,a)(u,x) = (pu, a+p(x))
u'=pu
x' = a + p(x)

x'₁ = 1+x₅
x'₂ = x₂
x'₃ = x₃
x'₄ = x₄
x'₅ = 1+x₉
x'₆ = 1+x₁
x'₇ = x₇
x'₈ = x₈
x'₉ = 1+x₆
x'₁₀ = x₁₀
x'₁₁ = x₁₁
x'₁₂ = x₁₂

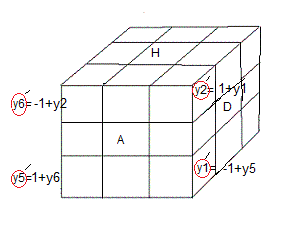
On retrouve bien la loi d'orientation pour les arêtes

examinons maintenant les sommets
Soit g=(q,b) l'état-sommet associé de la rotation A et t=(v,y)
permutation: q = 1->5->6->2
orientation: b = (-1,1,0,0,1,-1,0,0)

t'=gt
(v',y')=(q,b)(v,y)
gt = (q,b)(v,y) = (qv, b+q(y))
v'=qv
y' = b + q(y)

y'₁ = -1+y₅
y'₂ = 1+y₁
y'₃ = y₃
y'₄ = y₄
y'₅ = 1+y₆
y'₆ = -1+y₂
y'₇ = y₇
y'₈ = y₈




Ici on retrouve aussi la loi d'orientation pour les sommets.

Et voilà, on peut maintenant considèrer que G est un sous-groupe de G⁺.

Le centre de G: Z(G)

Le centre de G est des s' tels que ss'=s's pour tout s, on cherche donc s' qui a ainsi cette propriété. Voyons donc un peu ce qui donne:

(u,x,v,y)(u',x',v',y') = (u',x',v',y')(u,x,v,y)
(uu',x+u(x'),vv',y+v(y')) = (u'u,x'+u'(x),v'v,y'+v'(y))
d'où:
uu' = u'u ∀u ⇒ dans S₁₂ le seul élément qui commute avec tout le monde c'est u' = id (identité)

x + u(x') = x' + u'(x)
x - u'(x) = x' - u(x') comme c'est vrai pour tout x, on prend x=(0,0,0,0,0,0,0,0,0,0,0,0) d'où
x' = u(x') pour tout u, donc x'=(0,0,0,0,0,0,0,0,0,0,0,0) ou x'=(1,1,1,1,1,1,1,1,1,1,1,1) (on n'a pas d'autre choix pour x')

on fait exactement le même raisonnement pour v et y d'où
vv' = v'v ∀v ⇒ dans S₈ le seul élément qui commute avec tout le monde c'est v' = id (identité)
y - v'(y) = y' - v(y') comme c'est vrai pour tout y, on prend y=(0,0,0,0,0,0,0,0) d'où
y' = v(y') pour tout v donc y'=(0,0,0,0,0,0,0,0) ou y'=(1,1,1,1,1,1,1,1) ou encore y'=(2,2,2,2,2,2,2,2) (on n'a pas d'autre choix pour y')

mais on doit avoir
∑ x'_i = 0 (mod 2) ⇒ x'=(0,0,0,0,0,0,0,0,0,0,0,0) ou x'=(1,1,1,1,1,1,1,1,1,1,1,1) car 12=0 (mod 2)
et
∑ y'_i = 0 (mod 3) ⇒ seul y'=(0,0,0,0,0,0,0,0) convient
car y=(1,1,1,1,1,1,1,1) ⇒ 8=2(mod 3) et y=(2,2,2,2,2,2,2,2) ⇒ 16=1(mod 3) ne conviennent pas
finalement on a 2 solutions:
x'=(0,0,0,0,0,0,0,0,0,0,0,0), y'=(0,0,0,0,0,0,0,0) ou x'=(1,1,1,1,1,1,1,1,1,1,1,1), y'=(0,0,0,0,0,0,0,0) c-à-d
s'=(id,0,id,0)=e élément neutre du groupe, et s'=(id,1,id,0)=φ SuperFlip (tout reste invariant, seules les arêtes changent de l'orientation)
Z(G) = {e,φ} il n'y a que 2 éléments, en fait un seul élément φ car l'élément neutre e c'est évident qu'il est dans le centre.
et umumummuumbalallala et hop !!!!

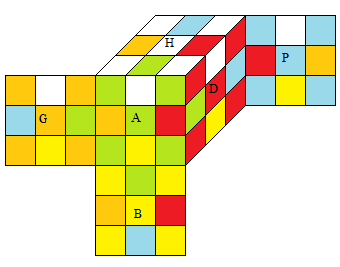SuperFlip φ = e•Φ Φ = D'H²PG' .AH'PBA .HB'GB² .A'DP'BA' .H'P'HB' (Mike Reid par ordinateur)

Michael Reid a trouvé cette formule (1995) Φ par ordinateur
Φ = D'H²PG' .AH'PBA .HB'GB² .A'DP'BA' .H'P'HB'
et Jerry Bryan (1995) démontre que c'est la plus courte formule du SuperFlip |Φ| = 24
φ = e•Φ

Note:
Déjà en 1992 Dik T. Winter a trouvé la formule Φ du SuperFlip à 20f (f-rotation, A²=1)
Φ = APH²DA².D²P²H'BA.H²D'G'HP².BD²HP²H
|Φ| = 20f
et (1995) Michael Reid démontre c'est le minimum pour f-rotation
φ = e•Φ

Un autre état intéressant c'est le 4Spot : face(A)<->face(P) et face(G)<->face(D)
Car il fait partie d'un état superloin (longueur=26) : le SuperFlip4Spot c'est le seul état superloin qu'on connait !!!

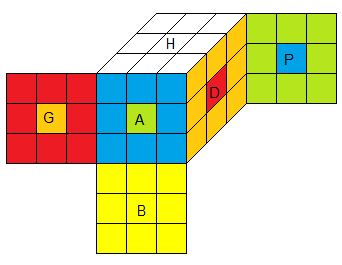4Spot ω = e•Ω Ω = BP²A²BH'G²D²H' = [ha][hd]

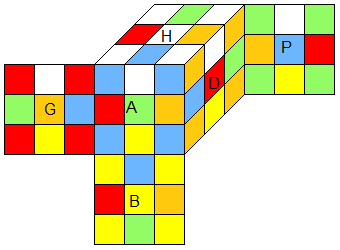	SuperFlip4Spot π = e•Π Π = H²B²G A² .H'BD² PH'B'D. GA²D HB' D'GHA'P'

1 2 3 4 [5] 6 7 8 9

Accueil

DMJ: 03/11/2024