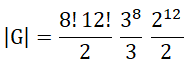La face cachée du Rubik's Cube

Le nombre d'états possibles

La première idée est se demander combien y-a-t-il d'éléments dans G ?, c-à-d combien y-a-t-il d'états possibles?
Avec les 3 loi qu'on vient de découvrir, on peut alors répondre à cette question:
1. La loi des twists dit ∑ y_i = 0 (mod 3) donc si 7 sommets sont bien orientés alors le 8ème aussi, sinon on aura ∑ y_i = 1 ou 2 (mod 3) donc on n'a besoin que Z₃⁷ au lieu de Z₃⁸
2. Même choses pour les arêtes, la loi des flips dit que ∑ x_i = 0 (mod 2) donc si 11 arêtes sont bien orientées alors la 12ème aussi, sinon on aura ∑ x_i = 1 (mod 2) donc on n'a besoin que Z₂¹¹ au lieu de Z₂¹²
finalement G est contenu dans
G ⊂ S₁₂ x Z₂¹¹ x S₈ x Z₃⁷

3. La loi de parité dit s=(u,x,v,y) avec sig(u)=sig(v)
posons:
K=S₁₂ x Z₂¹¹ x S₈ x Z₃⁷
et considèrons la fonction suivante:
f: K → {-1,1}
s=(u,x,v,y) → f(s) = sig(u).sig(v)
|K| / |Ker(f)| = |Im(f)|
or sig(u) = sig(v) ⇒ f(s)=1 ⇒ Ker(f) = G
d'où
|G| = |K|/2 = 12!.2¹¹.8!.3⁷/2 et ummuumumbalalala ....et hup !!!


NOTE : On a |G| - 1 = 43252003274489856000 - 1 = 43252003274489855999 est un nombre premier !!!, il est vraiment remarquable que |G| - 1 est premier car plus un nombre est grand moins il a de chance d'être premier !

Le GAP
Télécharger le GAP .::ICI::. https://www.gap-system.org/Releases/index.html
Dans la fenêtre de cmd on se place dans le dossier de GAP
C:\Users\nom> cd\gap4r4\bin
C:\gap4r4\bin>gap < gap_rubikcube.txt

ou bien
gap>
Ici on colle le text gap_rubikcube.txt

gap_rubikcube.txt: Permutations standards (arête,sommet)
p_H = (2,4,6,8)(26,28,30,32) (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
p_B = (18,24,22,20)(42,48,46,44) (9,15,13,11)(33,45,41,37)(35,47,43,39);
p_A = (2,34,18,36)(26,10,42,12) (1,35,11,23)(17,9,37,3)(19,33,39,21);
p_P = (6,38,22,40)(30,14,46,16) (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
p_G = (4,12,20,14)(28,36,44,38) (3,39,13,27)(21,11,41,5)(23,37,43,25);
p_D = (8,16,24,10)(32,40,48,34) (1,29,15,33)(17,31,45,35)(19,7,47,9);

Permutations étendues
p_Γ = (2,26);
p_Ψ = (1,17,19);
p_Ω = (2,8)(26,32);

Permutations tranches
p_h = (10,36,14,40)(34,12,38,16);
p_d = (2,30,22,42)(26,6,46,18);
p_a = (4,32,24,44)(28,8,48,20);

Le GAP nous donne bien
|G| = 43 252 003 274 489 856 000
|G⁺| = 519 024 039 293 878 272 000
|G⁺|/|G| = 12

Les facteurs de Jordan-Holder de G

Rappel: On dit qu'un groupe H est simple s'il ne possède pas des sous-groupes nornaux (autre que 1 et H bien sûr). G n'est pas 'simple' du tout !!!!
Un groupe qui n'est pas simple est "fabriqué" en quelque sort, par des groupes simples!! comme un nombre est composé par des nombres premiers.
Précisons un peu plus:
Soit H un groupe non simple, alors il existe une suite (appellée de décomposition) de sous groupes
H₀=1 ⊂ H₁ ⊂ H₂ ... ⊂ H_n = H avec H_k-1 normal dans H_k , tel que
1. H_k / H_k-1 = L_k simple

Remarque:
- H_k-1 doit être normal dans H_k, sinon on ne peut pas "diviser" les groupes !!!
- La condition: L_k est simple <==> H_k-1 est maximal

Les L_k sont des facteurs Jordan-Holder de H, qu'on notera JH(H)=L₁.L₂....
Note Le théorème de Jordan-Holder dit que toute suite de décomposition ayant la propriété 1. ci-dessus donne les même L_k, ce qui fait que H ne dépend pas des suites de décomposition mais seulement les L_k, les L_k sont donc les caractéristiques de H.
Exemple de groupes simples:
1. Groupe modulo: Z_p (p=premier) simple; en particulier Z₂,Z₃
2. Groupe Alterné: A_n (n>4) simple
et d'autres ....

Remarque
1. Si G₁,G₂ sont simples alors ===> on a : JH(G₁ x G₂)=G₁.G₂
2. JH(G) = JH(Ker(f)) . JH(Im(f)) où f est un morphisme

On a posé:
K=S₁₂ x Z₂¹¹ x S₈ x Z₃⁷ mais on peut regrouper autrement par exemple
=(S₁₂ x S₈) x (Z₂¹¹ x Z₃⁷) si on considère le morphisme g
g: S₁₂ x S₈ -> {-1,1}
(u,v) ----> g(u,v)=sig(u).sig(v) on voit que
G = Ker(g) x Z₂¹¹ x Z₃⁷ et si on considère encore une autre morphisme h
h: T -> {-1,1} avec T=Ker(g)
(u,v) ---> h(u,v) = sig(u) d'ou Ker(h)=A₁₂ x A₈ finalement
T/Ker(h) = Z₂ ===> Ker(g)/(A₁₂ x A₈) = Z₂ on a alors une suite JH de Keg(g)
1 ⊂ A₁₂ ⊂ A₁₂ x A₈ ⊂ Ker(g)
D'où les facteurs JH de Ker(g) est
JH(T)=A₁₂.A₈.Z₂ (on peut dire aussi: JH(T) = JH(Ker(h)).JH(Im(h)) )
et finalement les facteurs JH de G vaut

JH(G)=A₁₂.A₈.Z₂¹².Z₃⁷ (G est fabiqué à partir de A₁₂.A₈.Z₂¹².Z₃⁷)
d'où:
|G| = (12! . 8! . 2¹² . 3⁷)/4 = 43 252 003 274 489 856 000 = 2²⁷ 3¹⁴ 5³ 7² 11


Résumons:
1. Définition de G: G=l'ensemble des états produits par les rotations {H,B,A,P,G,D}.

2. G ⊂ S₁₂ x Z₂¹² x S₈ x Z₃⁸
(u,x,v,y) vérifiant
a. ∑ x_i = 0 (mod 2)
b. ∑ y_i = 0 (mod 3)
c. sig(u)=sig(v)

3. G = Ker(g) x Z₂¹¹ x Z₃⁷
où g: S₁₂ x S₈ -> {-1,1}
(u,v) → g(u,v)=sig(u).sig(v)

4. Les facteurs de Jordan-Holder: JH(G)=A₁₂.A₈.Z₂¹².Z₃⁷

5.

1 2 3 [4] 5 6 7 8 9

Accueil

DMJ: 03/11/2024