La face cachée du Rubik's Cube

Les quaternions

Ici vous arivez au pays des merveilles ... Comment un quaternion peut-il entrer dans un truc comme ça ? ... dans un Rubik's Cube !!! mais je rêve .....
Voyons de plus près, rappelons ce que c'est un quaternion. C'est un monbre complexe "généralisé" , en fait c'est un corps non commutatif contanant C découvert par Hamilton (le dernier corps construit à partir de Rⁿ). Un quarternion c'est quelque chose comme ça:
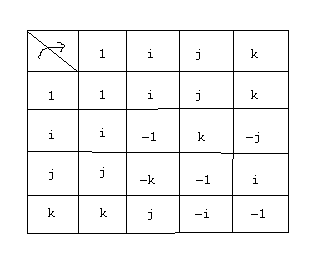
q = a + bi + cj +dk où a,b,c,d sont des rélles et i,j,k vérifiantt les relations suivantes:
On appelle le groupe quaternion c'est:
Q = { 1, i, j, k, -1, -i, -j ,-k }
Ce groupe est caractérisé par les propriétés suivantes:
i⁴ = 1, i² = j² , iji = j (*) (par définition: ij=k)

Soit maintenant les 2 états suivants
a = (u,x,id,0) où u = (1,4)(2,3) et x=(1,0,1,0,0,0,0,0,0,0,0,0)
b = (p,z,id,0) où p = (1,2)(3,4) et z=(1,0,0,1,0,0,0,0,0,0,0,0)

Pour ne pas alourdir les écritures on prend seulement le début de a et b la partie "arête" et seulement le Haut
a = (u,x) où u = (1,4)(2,3) et x=(1,0,1,0)
b = (p,z) où p = (1,2)(3,4) et z=(1,0,0,1)

a² = (u,x)² = (u²,x+u(x))
détaillons pour le calcul a²
permutation: u²=id c'est clair
orientation: x + u(x)
x₁+x₄ = 1+0=1
x₂+x₃ = 0+1=1
x₃+x₂ = 1+0=1
x₄+x₁ = 0+1=1
d'où
a² = (id,1,1,1,1)
On fait la même chose pour b

b² = (p,z)² = (p²,z+p(z))
permutation: p²=id c'est clair
orientation: z + p(z)
z₁+z₂ = 1+0=1
z₂+z₁ = 0+1=1
z₃+z₄ = 0+1=1
z₄+z₃ = 1+0=1
d'où
b² = (id,1,1,1,1)
et
a⁴ = (id,0,0,0,0)

aba = (u,x)(p,z)(u,x)

ab=(up, x+u(z))
permutation: up=(1,4)(2,3)(1,2)(3,4)=(1,3)(2,4)
orientation: x'= x + u(z)
x₁+z₄ = 1+1=0
x₂+z₃ = 0+0=0
x₃+z₂ = 1+0=1
x₄+z₁ = 0+1=1

(upu, x'+up(x))
permutation: upu=(1,3)(2,4)(1,4)(2,3)=(1,2)(3,4) = p
orientation: x' + (up)(x)
x'₁+x₃ = 0+1=1
x'₂+x₄ = 0+0=0
x'₃+x₁ = 1+1=0
x'₄+x₂ = 1+0=1
= (p,z) = b (wwoaaowwww !! )

d'où
aba=b

On a donc des correspondants:
a² = (id,1,1,1,1) = -1
a⁴ = (id,0,0,0,0) = 1

a et b vérifient toutes les relations (*), l'ensemble K = < a,b > est alors isomorphe à Q avec isomorphisme f défini par
f : K → Q
f(a) = i
f(b) = j
Autrement dit on identifie a = i , b = j, et par définition on pose ij = k , nul ne peut soupçonner que les motifs suivants représentent le groupe des quaternions Q = { 1, i, j, k, -1, -i, -j, -k } c'est-à-dire l'entier -1, le nombre complexe i, le quaternion j ... !!!!

On pose :
C = DP'AD'PA'HPHP'AD'A'D' (minimale,14)
J = G'DPH'P'HGPGHG'P'D'H' (minimale,14)
K = PHGH²G'P'H'D'H²D (minimale, 12)
N = A'H'G'HP'H²PGHAH'DH²D' (minimale,16)

Remarque : Le programme Cube Explorer fournit la formule lorsqu'on lui donne le motif. C'est avec ce programme que j'ai pu trouver les formules T et J pour a et b

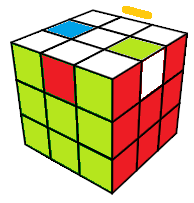
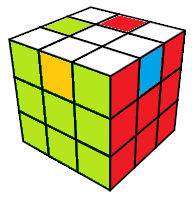
i=e•C C=(HA,HD°)(HG°,HP)	complexe j=e•J J=(HA,HG°)(HP°,HD)

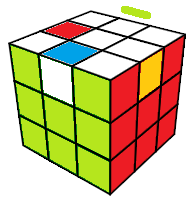
k=e•K K=(HA°,HP)(HG°,HD)	-1=e•N N=(HA)°(HG)°(HP)°(HD)°

l'entier -1, nombre complexe i, quaternion j, quaternion k

Résumons :
Seule la partie d'arête-Haut
i = (u,x) où u = (1,4)(2,3) et x=(1,0,1,0)
j = (u,x) où u = (1,2)(3,4) et x=(1,0,0,1)
k = ij = (u,x) où u=(1,3)(2,4) et x=(0,0,1,1)
i² = (u,x) où u = id et x=(1,1,1,1) 4 arêtes Haut flippées = MiniFlip

1 2 3 4 5 [6] 7 8 9

Accueil

DMJ: 16/05/2023