Le GAP et Rubik's Cube

Difficulté: 1/20 facile-

Calcul le nombre d'états du Pocket

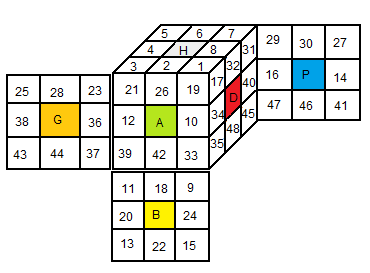
Autocollant numérotés

Voici un programme en GAP qui calcule le nombre d'états du Pocket :

Pocket :

# gap_pocket.txt # 5 6 7
# 4 H 8
# 3 2 1
#25 28 23|21 26 19|17 32 31|29 30 27
#38 G 36|12 A 10|34 D 40|16 P 14
#43 44 37|39 42 33|35 48 45|47 46 41
# 11 18 9
# 20 B 24
# 13 22 15

# Iso=le groupe isometrie du cube (48)
j1 := (6, 46, 18, 26)(8, 14, 24, 12)(38, 48, 36, 32)(2, 30, 22, 42)(16, 20, 10, 4)(28, 40, 44, 34)
(5, 45, 11, 17)(7, 13, 9, 3)(21, 31, 41, 35)(43, 33, 23, 29)(1, 25, 15, 37)(47, 39, 19, 27) ;

j2 := (6, 16, 22, 14)(8, 24, 20, 4)(38, 30, 40, 46)(2, 10, 18, 12)(28, 32, 48, 44)(34, 42, 36, 26)
(5, 31, 15, 43)(7, 45, 13, 25)(21, 19, 33, 39)(1, 35, 11, 23)(47, 41, 27, 29)(3, 17, 9, 37);

Iso := Group(j1,j2) ;

# Dep=le groupe isometrie+ du cube (24) ssg de Iso
d1 := (1,11)(2,18)(3,9)(4,24)(5,15)(6,22)(7,13)(8,20)(10,12)
(14,16)(17,37)(19,39)(21,33)(23,35)(25,45)(26,42)(27,47)(28,48)(29,41)
(30,46)(31,43)(32,44)(34,36)(38,40);

d2 := (1,15)(2,22)(3,13)(4,20)(5,11)(6,18)(7,9)(8,24)(10,16)(12,14)
(17,45)(19,47)(21,41)(23,43)(25,37)(26,46)(27,39)(28,44)(29,33)(30,42)
(31,35)(32,48)(34,40)(36,38);

d3 := (1,17,19)(2,32,10)(3,31,33)(4,40,42)
(5,45,39)(6,48,12)(7,35,21)(8,34,26)(9,23,29)(11,25,47)(13,43,41)
(14,22,44)(15,37,27)(16,18,28)(20,38,46)(24,36,30);

d4 := (1,35,11,23)(2,10,18,12)(3,17,9,37)(4,8,24,20)(5,31,15,43)
(6,16,22,14)(7,45,13,25)(19,33,39,21)(26,34,42,36)(27,29,47,41)
(28,32,48,44)(30,40,46,38) ;

Dep := Group(d1, d2,d3,d4) ;

# Pocket=le groupe Pocket (= Rubik sans arêtes)
pH := (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
pB := (9,15,13,11)(33,45,41,37)(35,47,43,39);
pA := (1,35,11,23)(17,9,37,3)(19,33,39,21);
pP := (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
pG := (3,39,13,27)(21,11,41,5)(23,37,43,25);
pD := (1,29,15,33)(17,31,45,35)(19,7,47,9);
pPsi := (1,17,19);

# Rubik=le groupe du Rubik's Cube
#pH := (2,4,6,8)(26,28,30,32) (1,3,5,7)(17,21,25,29)(19,23,27,31) ;
#pB := (18,24,22,20)(42,48,46,44) (9,15,13,11)(33,45,41,37)(35,47,43,39);
#pA := (2,34,18,36)(26,10,42,12) (1,35,11,23)(17,9,37,3)(19,33,39,21);
#pP := (6,38,22,40)(30,14,46,16) (7,25,13,45)(29,27,41,47)(31,5,43 ,15);
#pG := (4,12,20,14)(28,36,44,38) (3,39,13,27)(21,11,41,5)(23,37,43,25);
#pD := (8,16,24,10)(32,40,48,34) (1,29,15,33)(17,31,45,35)(19,7,47,9);
#pGamma := (2,26);
#pPsi := (1,17,19);
#pOmega := (2,8)(26,32);
#ph := (10,36,14,40)(34,12,38,16);
#pd := (2,30,22,42)(26,6,46,18);
#pa := (4,32,24,44)(28,8,48,20);

LAMBDAPLUS := Group( pH, pB, pA, pP, pG, pD, pPsi ); LAMBDA := Group( pH, pB, pA, pP, pG, pD ); Print( "\n" ); Print( "|LAMBDA+| = ",Size( LAMBDAPLUS ), "\n" ); Print( "|LAMBDA| = ", Size( LAMBDA ) , "\n" ); Print( "N = ", 3 , "\n" ); Print( "|G+| = ", Factorial(8) * (3^8) , "\n" ); Print( "|G| = |G+|/N = ",( Factorial(8) * (3^8) ) / 3 , "\n" );

1 2 3 4 [5] 6 7 8 9

Accueil

DMJ: 22/02/2024