L'algorithme minimal du Skewb
12
Dec
2013
Par morphocode
La découverte de cet algorithme minimal est tout à fait par hasard.
Le mécanisme interne (le core) du Skewb divise les sommets en 2 clans: {A,P,O,E} et {G,D,B,H}
ceux qui sont attachés au core et ceux qui sont libres, les libres ne peuvent pas se mettre à la place des attachés donc tout se passe
à l'intérieur du clans. En observant les effects du commutateur [DG'] sur le Skewb, en particulier sur le clan {A,P,O,E},
il gènère une permutation du type u=(A,P)(O,E) qui donne donc une idée de l'algorithme
1- Notation
Les centres seront notés entre parenthèses :
(H)aut, (B)as, (A)vant, (P)ostérieure, (G)auche, (D)roite.
Les rotations
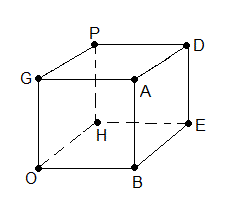
Voici les rotations (par rapport aux sommets):
(HDA) = A, (HPD) = D, (HGP) = P, (HAG) = G
(BAD) = B, (BDP) = E, (BPG) = H, (BGA) = O
G = tourner 120° le
sommet Gauche dans le sens horaire.
G' = tourner -120° le
sommet Gauche
tH = tourner le cube entier 90° suivant la face H, abrégé : tourner le cube suivant H
tH' = tourner le cube entier -90° suivant la face H, abrégé : tourner le cube suivant H'
tH² = tourner le cube entier 180° suivant la face H, abrégé : tourner le cube suivant H²
 |
 |
| rotations par rapport aux sommets |
rotation tH |
 |
 |
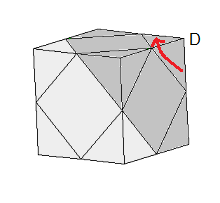| Rotation G |
Rotation D |
 |
 |
| Rotation A |
Rotation P |
On a choisi Haut=blanc, Bas=jaune, Avant=vert, Postérieur=klein, Gauche=orange, Droite=rouge
On se place en position de START
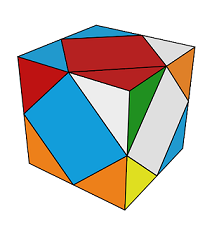
Position START (isoler les sommets)
Les 4 sommets blancs sont en Haut.
 |
|
| Position START : Les 4 sommets blancs sont en Haut |
|
A- Placer les sommets Haut
On place correctement les sommets Haut avec [DG']=(A,P)
 |
|
| placer correctement les sommets Haut |
|
Remarque : Une fois les sommets Haut sont bien placés, les sommets Bas sont automatiquement bien placés.
B- Placer des centres
On déplace les centres répèrés par les sommets, en utilisant la formule suivante:
Permutation circulaire de 3 centres:
(H)->(D)->(A) = [DG']²
On tient le cube comme il le faut pour appliquer la formule.
On essaie d'abord de placer le centre Haut (blanc) puis d'avoir 2 centres adjacents à (H),
Ensuite pour le centre Bas (jaune) c'est pareil , on retourne le cube (les sommets jaunes en Haut) et on fait la même chose
 |
|
| (H)->(D)->(A) = [DG']² |
|
C- Pivoter les sommets
Pour cela on utilise la formule suivante:
Pivoter 2 sommets:
O
-E
+ = [DG']
3 tH² [DG']
3
On tient le cube comme il le faut pour appliquer la formule.
 |
|
| [DG']3 tH² [DG']3 |
|
Formule supplementaire
Voici quelques formules intéressantes:
 |
 |
| (AGA' D'.AG' A' D)² |
[BD'][B'G] ou bien [DG']3 |
|
|
| [DG']3 tH² [DG']3 tH² = [DG']3[GD']3 |
|
Commentaire
Il est vraiment remarquable que le Skewb possède un algorithme minimal à une seule formule [DG'] !
comme le Rubik's Cube
En résumé:
¤ Placer en position START
L'algorithme minimal:
- Placer des sommets Haut : [DG']
- Déplacer 3 centres : [DG']²
- Pivoter 2 sommets : [DG']
3 tH² [DG']
3
1 2 [3] 4
Accueil
DMJ: 21/08/2022
