Résolution du Windmill

21 Dec 2013

Méthode la Croix (Jessica Fridrich) La résolution se fait exactement comme pour le Rubik's Cube, à deux exceptions près: savoir pivoter les centres, fixer les états singuliers.
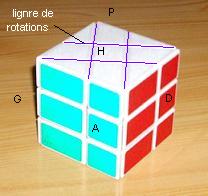
Il y a 2 centres carrés on va en choisir un comme le Haut. Donc pour nous le Haut c'est le centre carré blanc

Notation:

On va nommer les faces et les couleurs ainsi:
H(aut)=b(lanc) , B(as)=j(aune) , A(vant)=v(ert) , P(ostérieure)=k(lein) , G(auche)=o(range) , D(roite)=r(ouge)
d(droite-intérieur) .

Les rotations
A = tourner 90° la face Avant dans le sens des aiguilles d'une montre.
A' = tourner 90° dans le sens contraire
A² = tourner 180°
D* = tourner le bloc Droite
d = droite-intérieur (d=D*D')

Dans les dessins 3D, la face Haut a le carré blanc .
On écit (HA) pour désigner l'arête Haut-Avant ou (HDA) le sommet Haut-Droite-Avant
(HA)° = pivoter l'arête (HA)
(HDA)° = pivoter le sommet (HDA)
Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!


Rotation: ADA'D'. H² . G'

A- Faire la Croix

Aucun problème.


Même couleurs entre l'arête et centre

B- Placer des sommets

Aucun problème.
Placer: (BAD)->(HDA)=ABA'
Pivoter: (HDA)°=D'BDABA'

C- Faire le 2ème étage (l'équateur)

Retournez le cube (Haut -> Bas et Bas -> Haut).
Utiliser [HD][H'A'] ou [H'A'][HD] pour ranger les 4 arêtes de l'équateur.

Et voici 2 formules pour pivoter les centres:
(H)²⁺ = (HDGH²D'G')²
(H)⁺(G)^- = Hd'h'd .H'd'hd
Remarque : On peut pivoter les centres à la fin, quand tout est fini.

D- Placer les sommets

D'abord on veut seulement placer les sommets, l'orientation on verra.
Echanger deux sommets
(HAG)<->(HDA)=PH' A' HP' H' AH²

On va maintenant orienter les 2 sommets-adjacents. Monter les 2 couleurs Avant vers Haut
Remarque: Si les sommets sont en opposés on remplace H' = H = H² dans la formule
(HAG)°(HDA)° = (D'BDABA') .H'(AB'A'D'B'D)H

E- Ranger les arêtes

Déplacer 3 arêtes:
(HA)->(HP)->(HD) = D². HAP'.D².PA'H.D²
Pivoter 2 arêtes:
(HA)°(HD)° = AH²A².B'[H'G']B.A²H'A'H'

F- Les états singuliers

A cause de la symétrie (invariant par les rotations) de certains centres: 2 centres carrés ... Le Windmill gènère une singularité sur les centres.

1. Pivoter un centre à 90°.
Il suffit alors de pivoter avec un centre carré: G=centre à pivoter et H=centre carré
(H)⁺(G)^- = Hd'h'd .H'd'hd


(H)⁺(G)^- = Hd'h'd .H'd'hd

Explication sur l'état singulier
Comme il y a des centres symétriques (ça change rien si on les pivote) les 2 centres carrés . Lorsqu'on mélange le cube on les pivote avec d'autres centres ce qui fait qu'on ne voit qu'un seul centre qui change d'où la singularité. Donc pour pivoter un centre à 90° dans la formule
(H)⁺(G)^- = Hd'h'd .H'd'hd
on choisit G = "le centre à pivoter" et H un centre carré (invariant par rotation) , et le tour est joué!