Résolution du Void Cube
17
Dec
2014
La résolution du Void Cube se fait exactement comme un Rubik's Cube, sauf à 2 détails prés:
1. Déterminer la couleur des centres
2. Fixer la singularité(°)
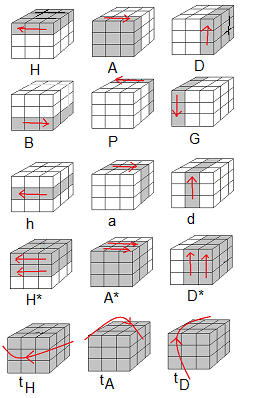
Rotations de base (standard) : {H,h,a,P,G,D} ; on veut que l'arête (BA) soit fixe
(°)Par définition : Un état singulier c'est un état quand on a un couple d'arêtes ou de sommets à échanger.
1- Notation
On va nommer les faces et fixer le Cube:
H(aut)=b(lanc), B(as)=j(aune), A(vant)=v(ert), P(ostérieur)=k(lein), G(auche)=o(range), D(roite)=r(ouge)
h(aut-intérieur) , a(vant-intérieur) , d(roite-intérieur).
Les rotations
A = tourner 90° la face Avant dans le sens des aiguilles d'une montre.
A' = tourner 90° dans le sens contraire
A² = tourner 180°
A* = tourner 90° le bloc Avant (2 tranches) dans le sens des aiguilles d'une montre.
a = tourner 90° la face avant-intérieur dans le sens des aiguilles d'une montre (a = A*A').
tH = tourner le cube entier suivant H.
Dans les dessins 3D, la face Avant porte la couleur
verte, et on voit le Haut (
blanc) et la Droite (
rouge).
On écit (HA) pour désigner l'arête Haut-Avant ou (HDA) le sommet Haut-Droite-Avant
(HA)° = renverser l'arête (HA)
(HDA)° = pivoter le sommet (HDA)
Le point '.' ou les parenthèses '(', ')' qui se trouvent dans les formules sont là pour faciliter la lecture c'est tout!!!
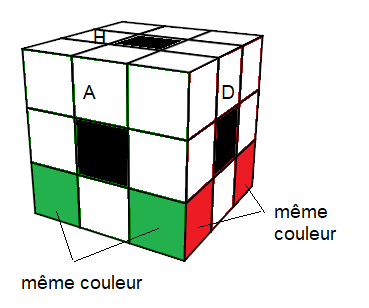
A- Finir les sommets Bas
Comme on ne connait pas la couleur des centres, on va donc adopter le style "POCKET" , on range d'abord les sommets Bas.
Si le sommet n'est pas bien orienté on le pivote (2 fois si nécessaire).
 |
 |
| Ce qu'on veut |
Les rotations |
 |
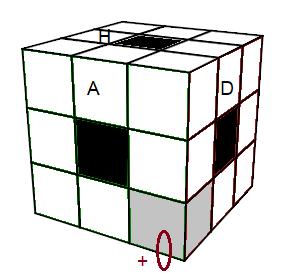 |
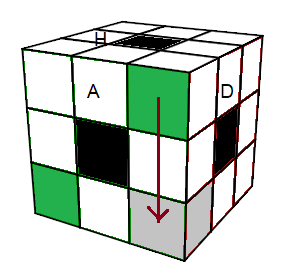
| (HDA)->(BAD) = [DH] |
(BAD)+ = [DH]² |
On va placer les sommets-Bas dans l'ordre suivant: (BAD), (BDP), (BPG) et (BGA) :
1. Choisissez un sommet-Bas , placez le en (HDA), puis descendez le en (BAD), s'il est mal orienté on le pivote avec [DH]²
2.
tH tourner le cube entier suivant H, on cherche alors le sommet qui a les couleurs Bas et Avant
3. Rangez le (placer et orienter)
4. Revenez au point 2.
Descendre: (HDA)->(BAD) = [DH]
Pivoter: (BAD)
+ = [DH]²
Remarque : si le sommet est en Bas on le remonte avec [DH]
B- Finir les arêtes Bas
 |
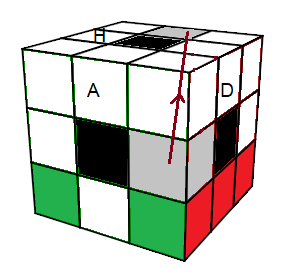 |
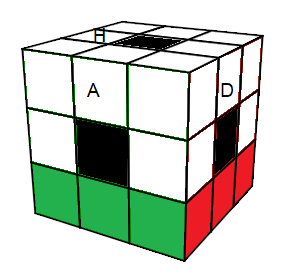
| Ce qu'on veut |
(AD)->Haut = (D'H')²(DH)² DH' ou
(AD)->Haut = [HD][H'A'] |
 |
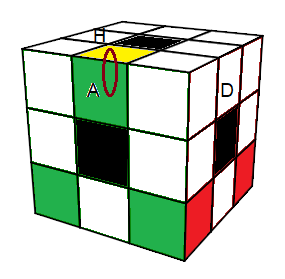 |
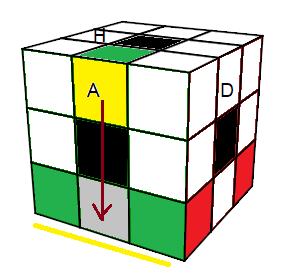
| (HA)->(BA) = [Hd] |
(HA)° = dHd'H |
Descendre: (HA)->(BA) = [Hd] (pour descendre il faut monter la chercher)
Renverser: (HA)° = dHd'H
Equateur->Haut:
(AD)->Haut = (D'H')²(DH)² DH' ; ou
(AD)->Haut = [HD][H'A']
Puis on continue la résolution normalement comme un Rubik's Cube
.::ICI::.
C- Les états singuliers
Par définition : Un état singulier c'est un état quand on a
un couple d'arêtes ou de sommets à échanger.
Le Void Cube peut produire de vrais états singuliers, voici 2 formules magiques qui corrigent la singularité.
(HA)<->(HD) = X = (aH)²(aH')²aH²(aH')² (arêtes)
Y = HD'G'H² GHG' H²DH'G (13); passer aux singularité-arêtes
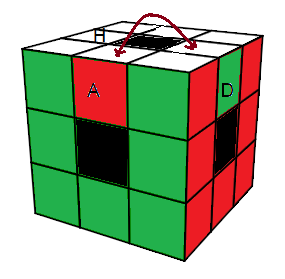 |
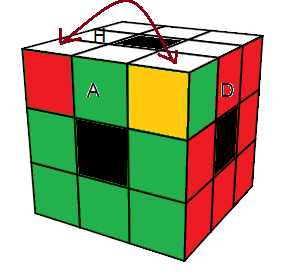 |
| X = (aH)²(aH')²aH²(aH')² (15) |
On utilise la formule Y pour passer aux arêtes |
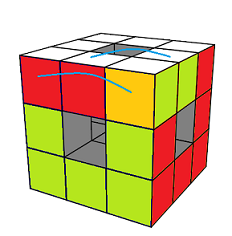 |
|
Y = HD'G'H² GHG' H²DH'G
passer aux singularité-arêtes |
|
Note
L'effet de X: échanger 2 arêtes (HA)<->(HD) et (H)->(G)->(B)->(D)
D- Explication de la singularité
Le Void Cube est le 1er Cube qui gènère de vrais états singuliers , c'est un phénomène vraiment intéressant, faites donc
une expérience...
Prenez un Rubik's Cube mélangé.
Placez le centre Avant=vert, (donc le centre Postérieur=klein) puis sélectionnez le centre
orange comme le
Bas
et placez l'arête (jv) en (BA) (faites comme si le centre Bas était jaune), puis les 3 autres arêtes (BD)=(jr), (BP)=(jk),
(BG)=(jo) comme indique la fig,
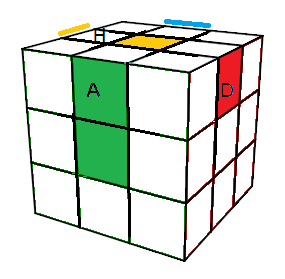 |
|
| centre Avant=vert et centre Bas=orange |
|
En suite résolvez le Cube normalement en répèrant les couleurs par rapport aux arêtes et non aux centres,
faites comme si les centres n'existent pas. A la fin vous verrez qu'il y a 2 arêtes (ou 2 sommets) à permuter !!!
voilà la singularité !
On voit que les centres se déplacent en 4-cycle !
fixons nous les yeux sur les centres, ils sont permutés,
ici, on a une permutation impaire de 4 centres (H)->(G)->(B)->(D) = (H,G)(H,B)(H,D), le Cube permute alors 2 arêtes
(permuter les centres revient à permuter les arêtes).
Donc si les centres ont une permutation impaire, alors on a aussi une permutation impaire pour les arêtes, c'est la singularité.
On voit donc on a 50% de chance de tomber sur ces états singuliers !!
Le fait de décider au hasard un centre est blanc parmis les 6 centres, revient à permuter les centres. Si par malheur on tombe sur une permutation impaire , alors on tombe sur ces états singuliers.
Que fait la formule X ?
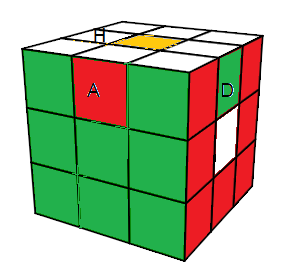
Prenez un Rubik's Cube normal, appliquez la formule X à l'état résolu et observons:
 |
|
| X = (aH)²(aH')²aH²(aH')² |
|
X permute 4 centres : (H)->(G)->(B)->(D) , et 2 arêtes (HA)<->(HD). On voit donc qu'on peut utiliser la formule X pour fixer la singularité-arêtes.
En résumé: Si les centres ont une permutation impaire alors on a un état singulier, donc on a 50% de chance d'avoir un état singulier.
Nous venons de découvrir la loi : "La signature des centres = la signature des arêtes" !!
D- REMARQUES
A)
Sur la résolution (importante) :
On a résolu le Void Cube avec des rotations non-standards {B,A,d, ...}. On peut se demander s'il est possible de résoudre le Cube avec uniquement des rotations standards
{H,h,a,P,G,D} ?
La réponse est positive.
Il suffit de remplacer les formules classiques par des formules contenant uniquement les rotations {H,h,a,P,G,D} , les voici :
1) Pour le Bas :
==> (HDA)->(BAD) = [DH], (BAD)
+ = [DH]²
==> (HD)->(BD) = [Ha'], (HD)° = a'HaH
==> pour monter l'arête-équateur (AD) vers le Haut : (AD)->(HP) = (D'H')²(DH)² DH'
2) Pour l'équateur :
==> on remplace [H'A'][HD] par : H'P'aDPa' .[HD]
==> on remplace [HD][H'A'] par : [HD] .H'P'aDPa'
3) Pour le Haut :
==> on remplace J = A[DH]A'H par K = H'DPH P'H'D'H²
==> (HGP)->(HAG)->(HPD) = [DH] .G'[HD]G
==> (HAG)°(HGP)° = [DH]² .G'[HD]²G
4) Pour la singularité-sommets on passe de la singularité-sommet en singularité-arête par la formule :
Y = HD'G'H² GHG' H²DH'G
B) Le vocabulaire (importante) :
Ici il s'agit de la singularité et non de parité (problème de parité), en effet le Void Cube n'a pas de loi de parité , donc on ne peut pas la violer !
Un état singulier est un état légal particulier "renommé" c'est tout !!, la preuvre qu'on obtient ces états uniquement par des rotations standards.
X = (aH)²(aH')²aH²(aH')²
Y = HD'G'H² GHG' H²DH'G
E- Formules supplémentaires
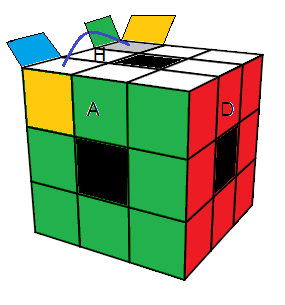
Voici une formule étendue (non-standard) pour fixer la singularité-sommets
 |
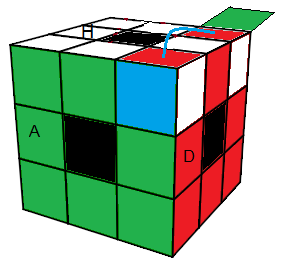 |
| (HAG,HGP) = GBDB'GP² D'HAH'D P²G²BD'H' (tH) |
(HDA,HPD) = P(P'HA'H2PH'A)² H'DPD' (a'H')4 DP'D'G² a G² a² P' |
1 [2]
Accueil
DMJ: 20/05/2025

















